Array Problems
- Problems
- Two Pointers:
- 1. Best time to buy and sell stock - LC 121 - Easy
- 2. Merge two sorted arrays - LC 88 - Easy
- 3. Intersection of 3 sorted arrays - LC 1213 - Easy
- 4. Running Sum of 1d Array - LC 1480 - Easy
- 5. Implement Merge Sort IK Problem
- 6. Two Sum - LC - 1 - Easy
- 7. Maximum Subarray - LC 53 - Easy
- 8. Remove Duplicates from sorted array - LC 26 - Easy
- 9. Concatenation of Array - LC 1929 - Easy
- 10. Contains Duplicate - LC 217 - Easy
- 11. Contains Duplicate - II - LC 219 - Easy
- 12. Two Sum Array is Sorted - LC 167 - Medium
- 13. Sort the array of integers - LC 912 - Medium
- 14. Boats to Save people - LC - 881 - Medium
- 15. Sort Colors or Dutch Flag Problem - LC 75 - Medium
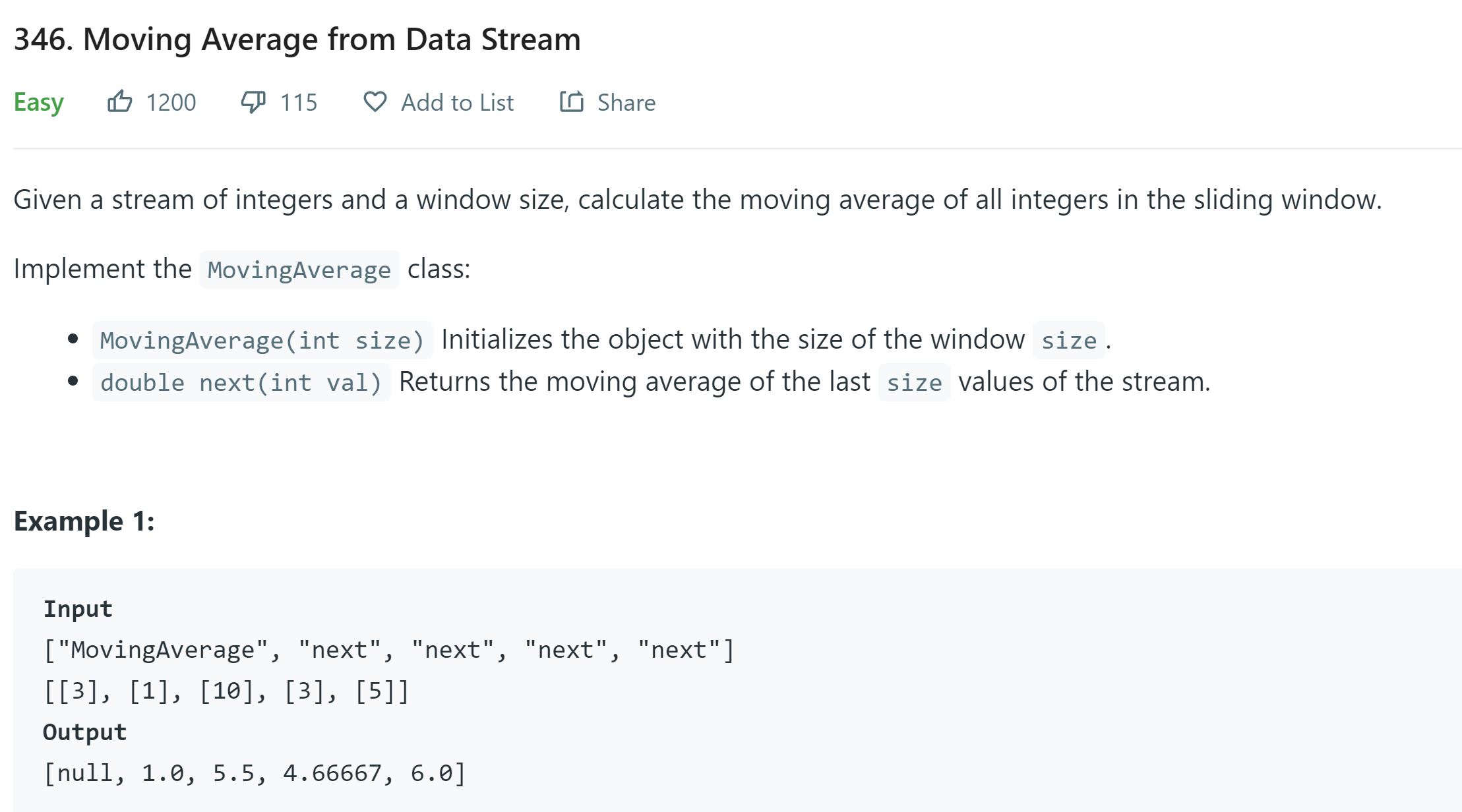
- 16. Moving Average from Data Stream - LC 346 - Easy
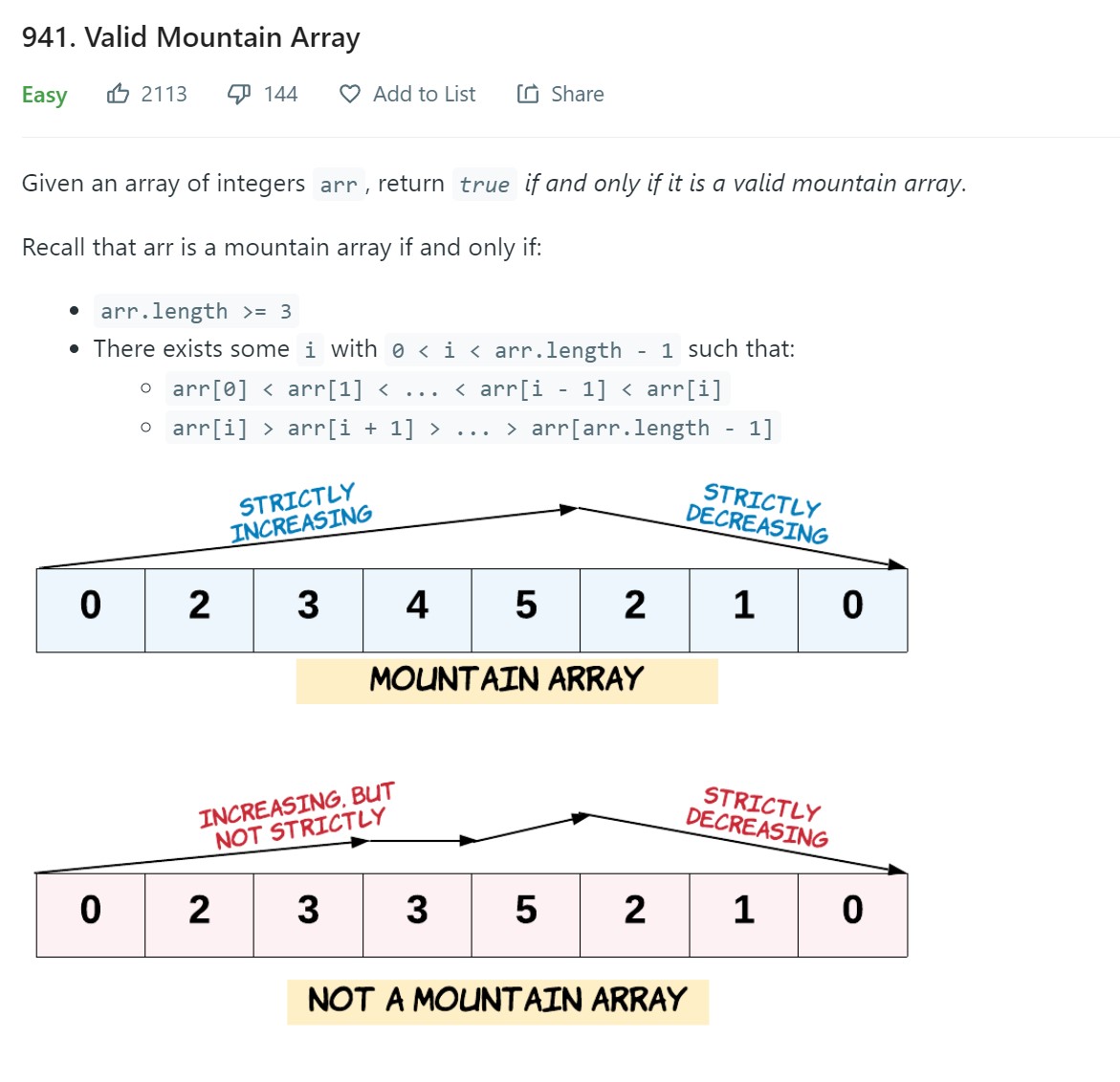
- 17. Valid Mountain Array - 941 - Easy
- Interval Line Sweep:
- Binary Search Variants:
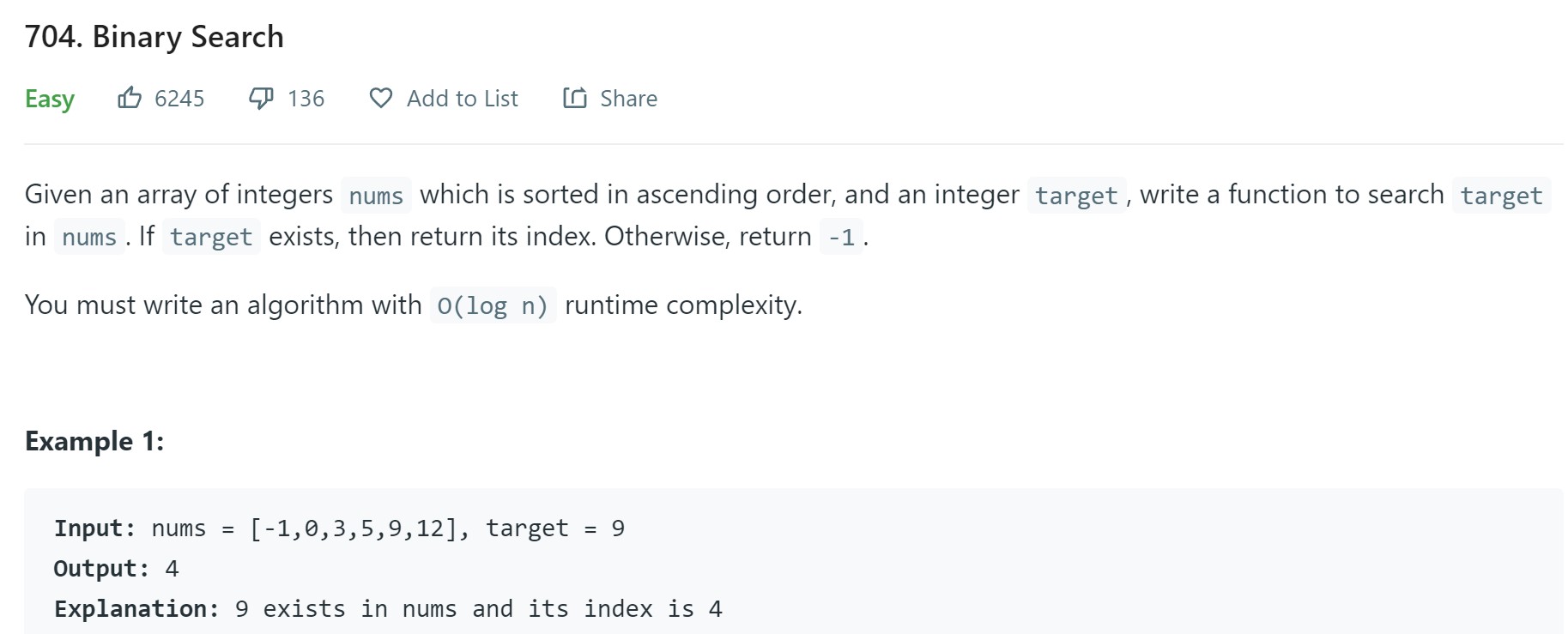
- 1. Binary Search - LC 704 - Easy
- 2. Guess the Number - LC 374 - Easy
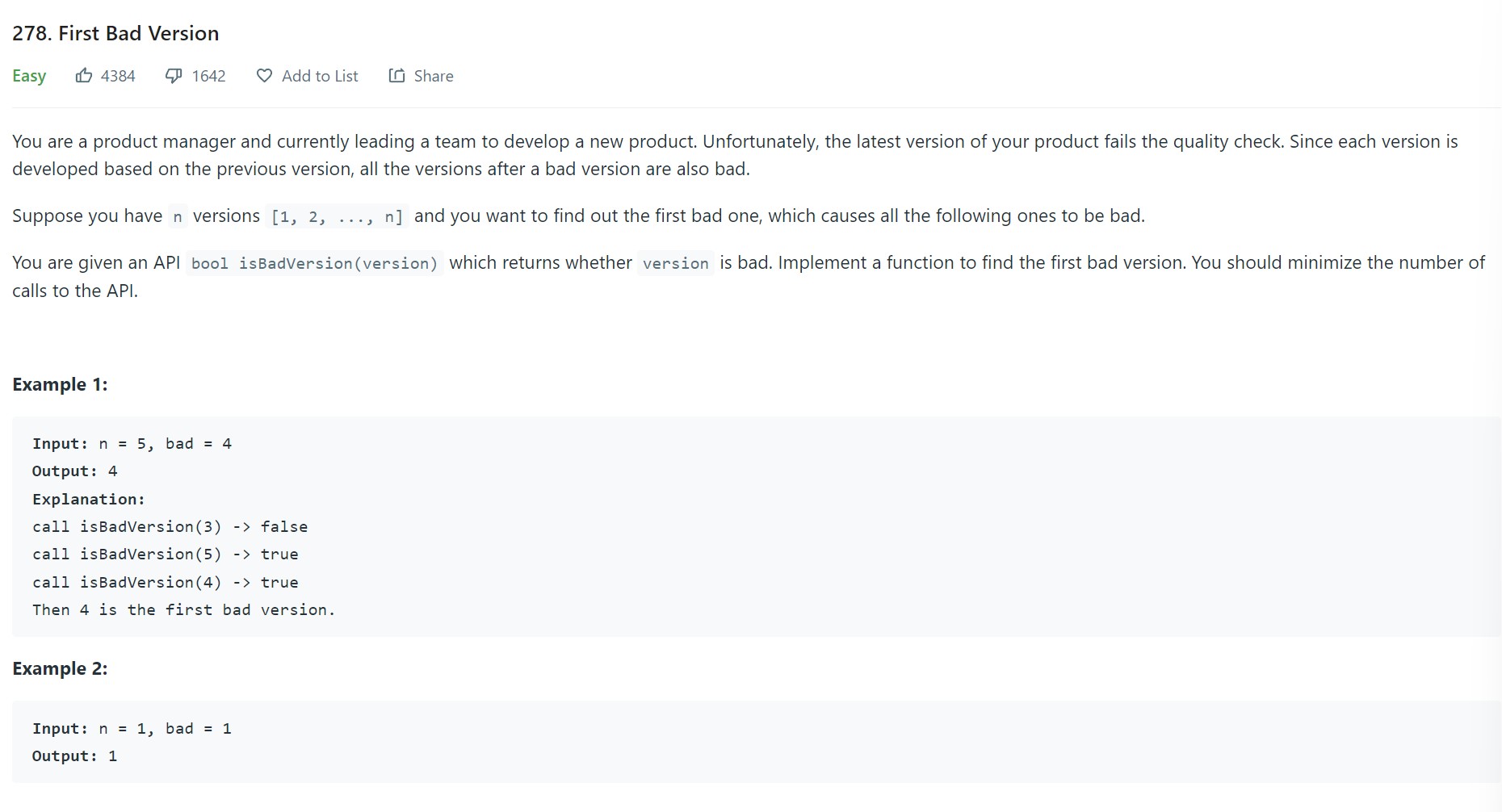
- 3. First Bad Version - LC 278 - Easy
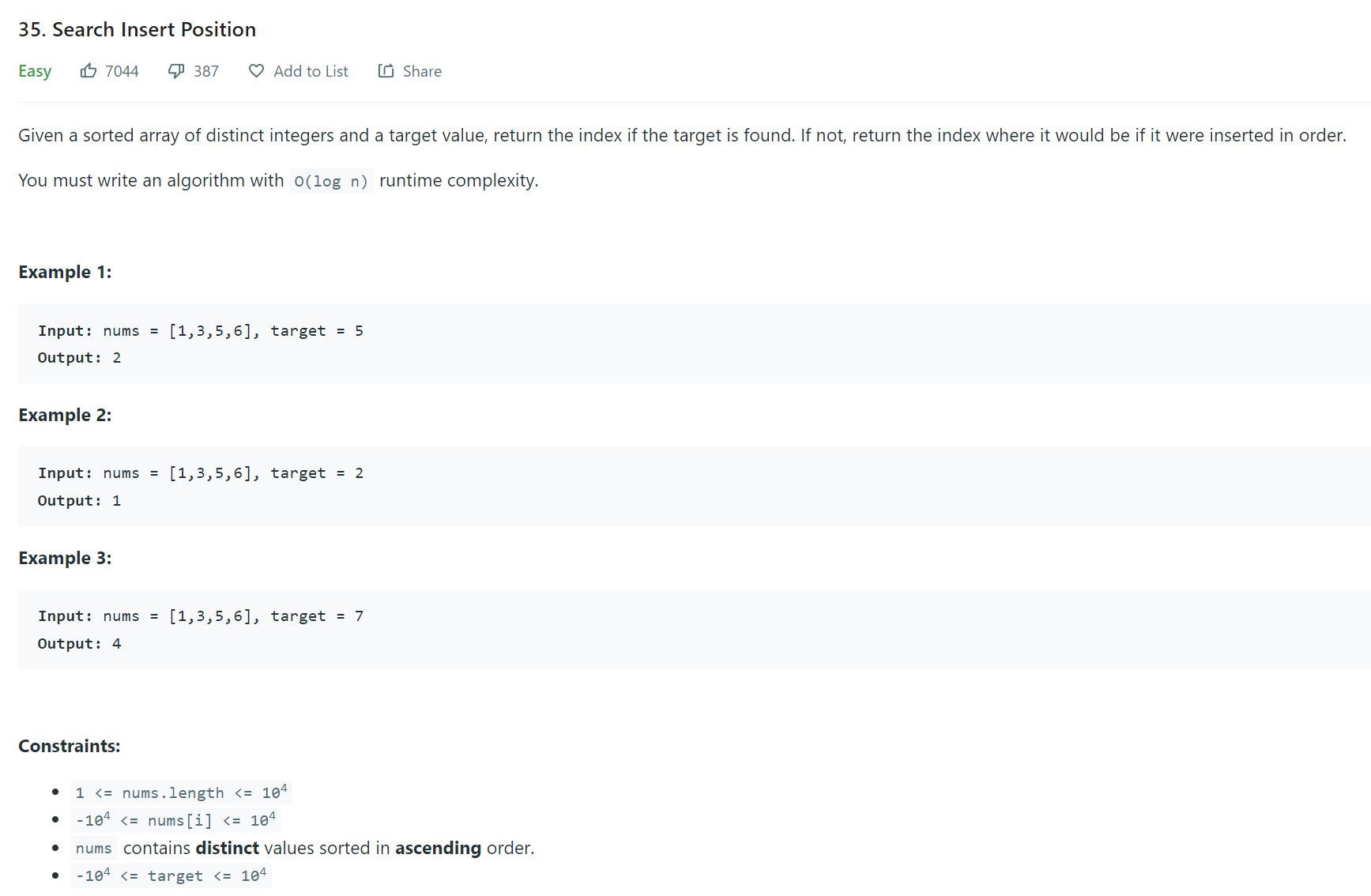
- 4. Search Insert Position - LC 35 - Easy
- 5. Find smallest letter greater than target - LC 744 - Easy
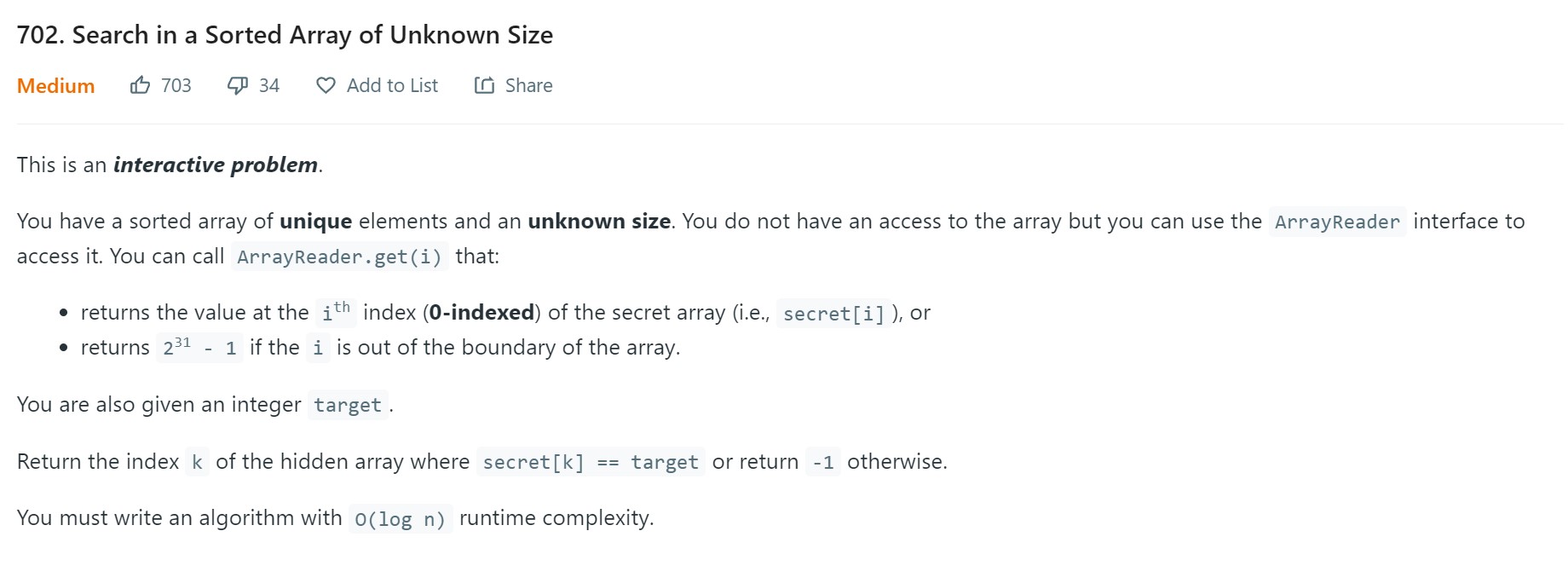
- 6. Search in a sorted array of unknown size - 702 - Medium
- 7. Peak index in a mountain array - 852 - Easy
- Cycle Sort Variants:
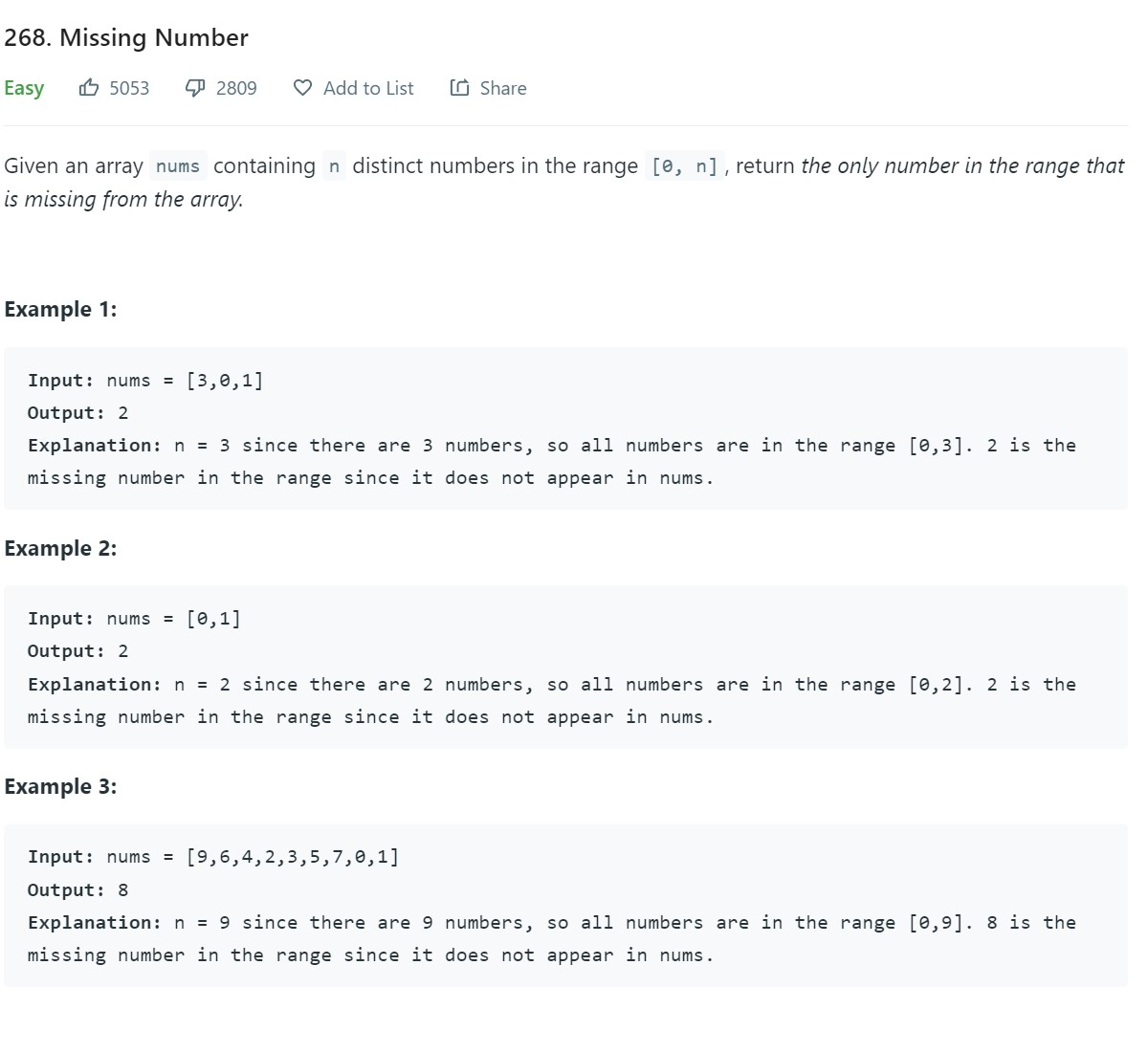
- 1. Missing Number - LC 268 - Easy
- 2. Find All numbers disappeared in an array - LC 448 - Easy
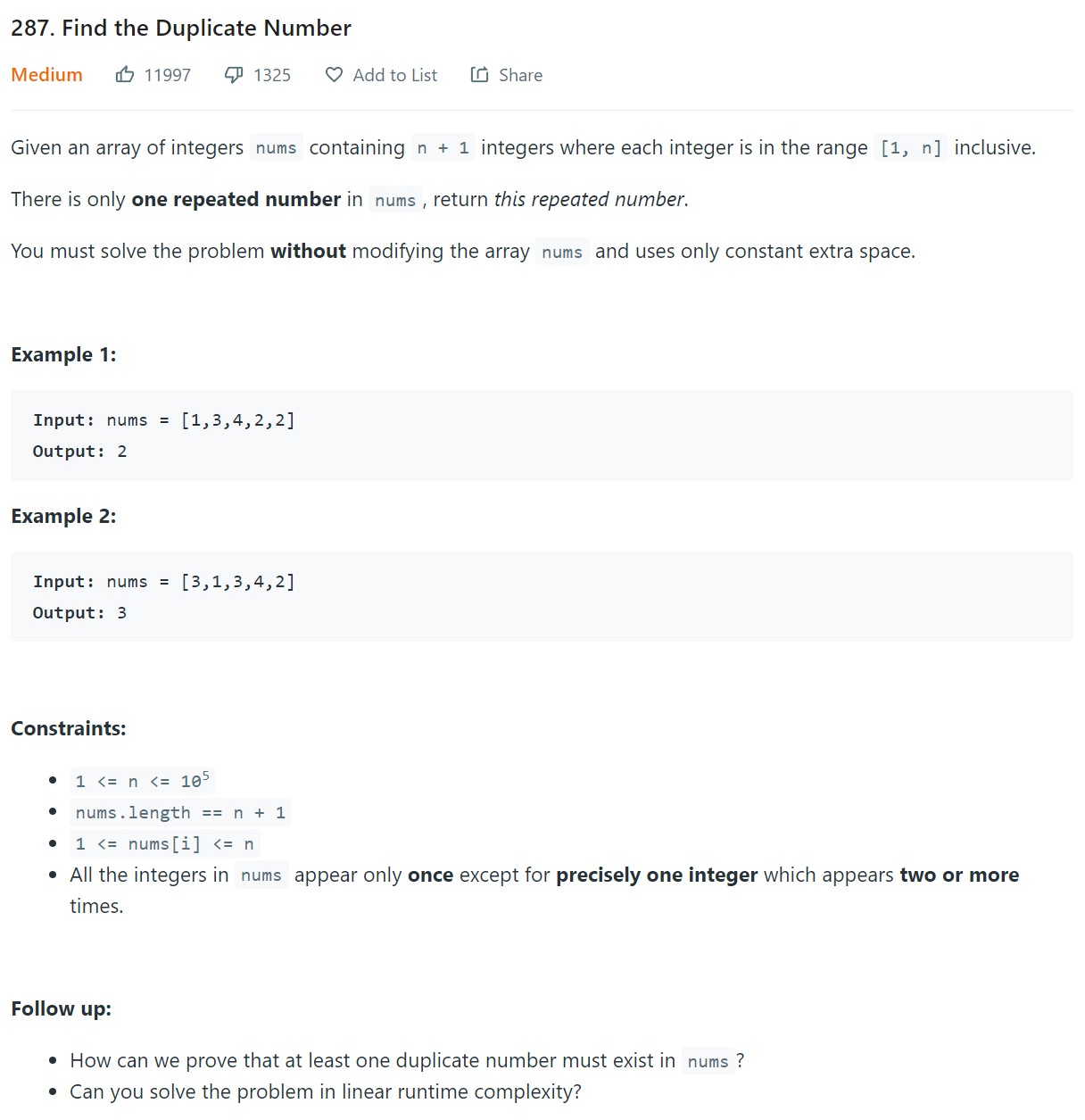
- 3. Find the duplicate number - LC 287 - Easy
- 4. Set Mismatch - LC 645 - Easy
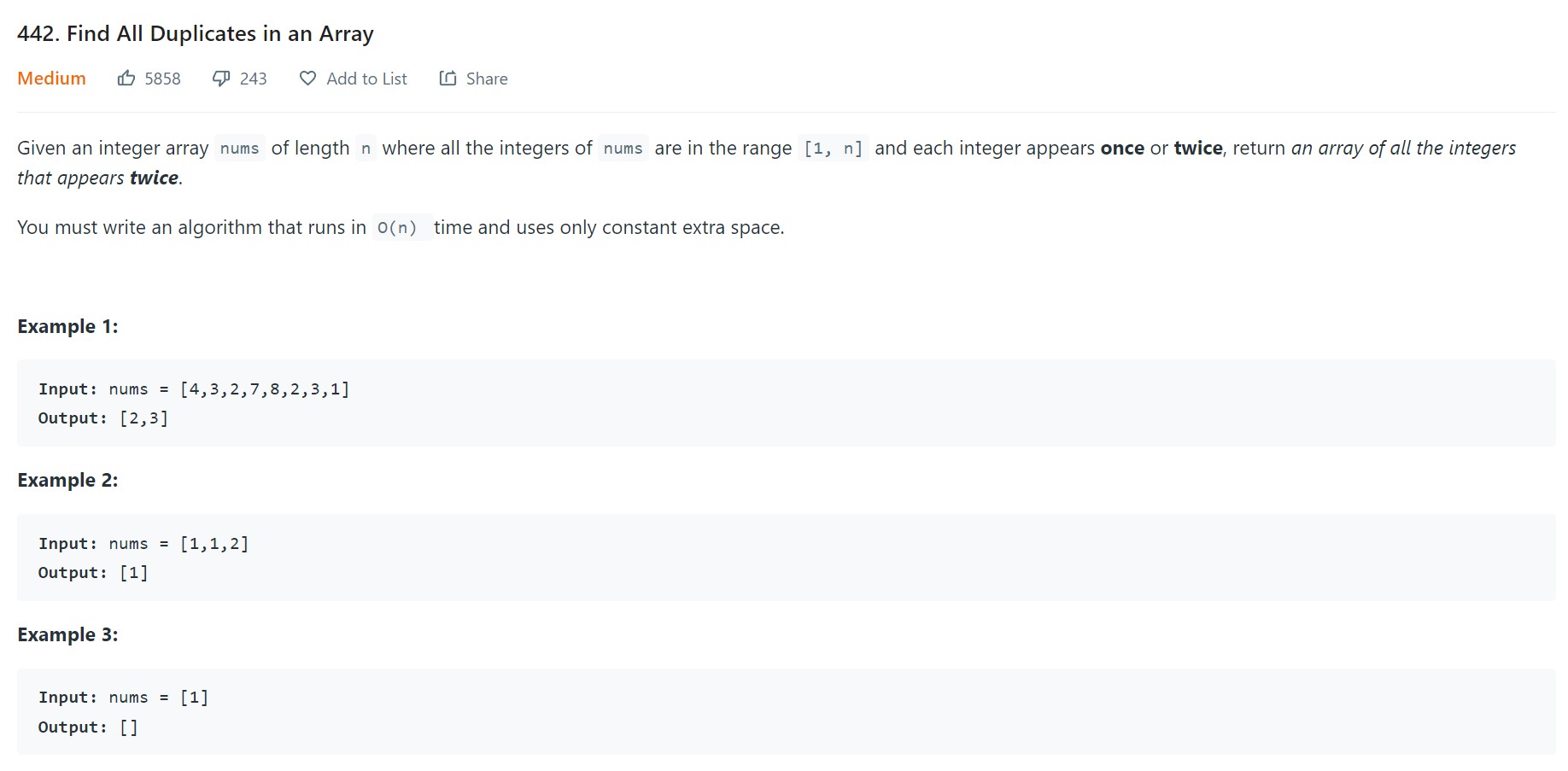
- 5. Find all duplicates in an array - 442 - Easy
- 7. Find first and last position of element in sorted array - 34 - Medium
- 8. Check if a number is majority element in a sorted array - 1150 - Easy
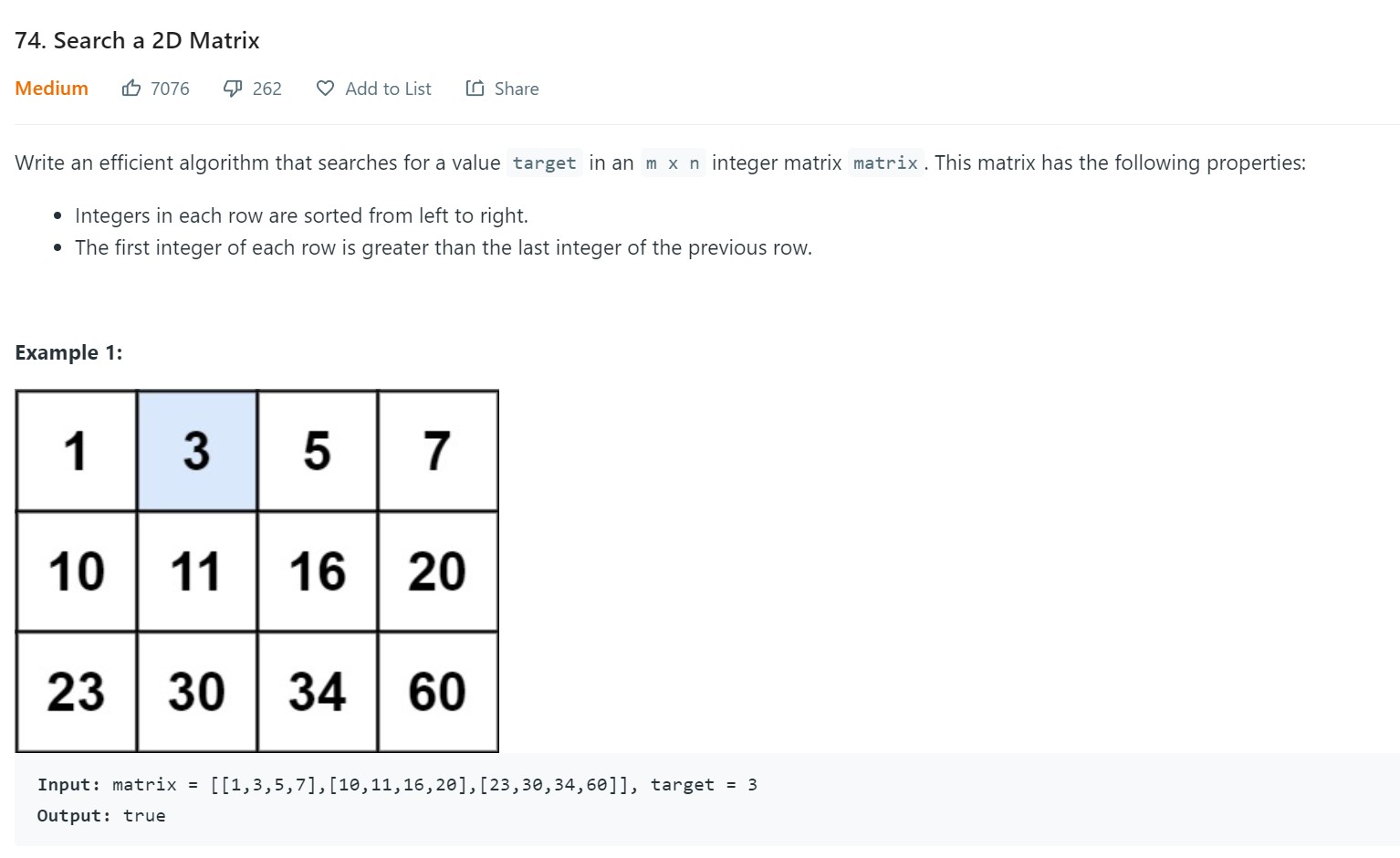
- 9. Search 2D matrix - 74 - Medium
- Prefix Sum Problems:
- Sliding Window - Fixed Length:
- Sliding Window - Variable Length
- 4. Longest Substring without repeating characters - LC 3 - Medium
- 5. Longest Substring with at most k distinct characters - LC 340 - Medium
- 6. Longest Substring with at most two distinct characters - LC 159 - Medium
- 7. Find all Anagrams in a string - 438 - Medium
- 8. Subarray product less than K - 713 - Medium
- 9. Minimum Operations to Reduce X to Zero - 1658 - Medium
- Unclassified
Problems
Two Pointers:
1. Best time to buy and sell stock - LC 121 - Easy

Clarification Questions
- Can I assume the array always contains at least two prices?" (This ensures we have a valid buying and selling opportunity.)
- Are there any constraints on the stock prices, such as a maximum value?" (This helps us understand the data range.)
Thought Process
- Brute Force Approach A straightforward approach is to try every possible combination of buying and selling days.
Logic: Use two nested loops. The outer loop iterates through the possible buying days, and the inner loop iterates through the possible selling days (after the buying day). Calculate the profit for each combination and keep track of the maximum profit.
- Optimized Approach We can optimize this by keeping track of the minimum price encountered so far while iterating through the array.
Logic: Initialize min_price to the first price and max_profit to 0. Iterate through the array, updating min_price if a lower price is found. Calculate the profit by subtracting min_price from the current price and update max_profit if a higher profit is found.
Code
# Brute Force Approach
def maxProfit(prices):
max_profit = 0
for i in range(len(prices) - 1):
for j in range(i + 1, len(prices)):
profit = prices[j] - prices[i]
max_profit = max(max_profit, profit)
return max_profit
# Optimized Approach
def maxProfit(prices):
min_price = float('inf')
max_profit = 0
for price in prices:
min_price = min(min_price, price)
max_profit = max(max_profit, price - min_price)
return max_profit
Complexity:
- Brute force Approach:
- Time Complexity: \(O(N^2)\)
- Space complexity: \(O(1)\)
- Optimized Approach:
- Time Complexity: \(O(N)\)
- Space complexity: \(O(1)\)
Test Cases
def test_max_profit():
assert maxProfit([7, 1, 5, 3, 6, 4]) == 5 # Example from the problem
assert maxProfit([7, 6, 4, 3, 1]) == 0 # No profit possible
assert maxProfit([1, 2]) == 1 # Simple increasing case
assert maxProfit([2, 4, 1]) == 2 # Buy on day 0, sell on day 1
assert maxProfit([3, 2, 6, 5, 0, 3]) == 4 # Buy on day 1, sell on day 2
2. Merge two sorted arrays - LC 88 - Easy

Clarification Questions
- Can I assume the arrays contain only integers?" (Understanding the data type is helpful.)
- Are there any constraints on the size of the arrays?" (This could influence your approach.)
- Could you provide an example to illustrate the expected output?" (Ensures you and the interviewer are on the same page.)
Thought Process
- The key is to start filling nums1 from the end, taking advantage of the extra space.
- Initialize three pointers: p1 pointing to the last actual element in nums1, p2 pointing to the last element in nums2, and p pointing to the last position in nums1.
- Compare the elements at p1 and p2. Place the larger element at position p in nums1.
- Move the corresponding pointer (p1 or p2) one step back.
- Decrement p.
- Repeat steps 2-4 until you’ve processed all elements in nums1 and nums2.
Code
# Solution from Gemini
def merge(nums1, m, nums2, n):
p1 = m - 1
p2 = n - 1
p = m + n - 1
while p1 >= 0 and p2 >= 0:
if nums1[p1] > nums2[p2]:
nums1[p] = nums1[p1]
p1 -= 1
else:
nums1[p] = nums2[p2]
p2 -= 1
p -= 1
# If there are remaining elements in nums2, copy them to nums1
nums1[:p2 + 1] = nums2[:p2 + 1]
# Solution from IK
class Solution:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
"""
Do not return anything, modify nums1 in-place instead.
"""
p = (m + n) - 1
p1 = m - 1
p2 = n - 1
while p >= 0:
if p2 < 0:
break
if nums1[p1] < nums2[p2]:
nums1[p] = nums2[p2]
p2 -= 1
p -= 1
else:
if p1 >= 0:
nums1[p] = nums1[p1]
p -= 1
p1 -= 1
else:
nums1[p] = nums2[p2]
p -= 1
p2 -= 1
Complexity:
- Time Complexity: \(O(m + n)\)
- Space complexity: \(O(1)\)
Test Cases
def test_merge():
nums1 = [1, 2, 3, 0, 0, 0]
m = 3
nums2 = [2, 5, 6]
n = 3
merge(nums1, m, nums2, n)
assert nums1 == [1, 2, 2, 3, 5, 6] # Basic case
nums1 = [1]
m = 1
nums2 = []
n = 0
merge(nums1, m, nums2, n)
assert nums1 == [1] # Empty nums2
nums1 = [0]
m = 0
nums2 = [1]
n = 1
merge(nums1, m, nums2, n)
assert nums1 == [1] # Empty nums1
3. Intersection of 3 sorted arrays - LC 1213 - Easy
class Solution:
def arraysIntersection(self, arr1: List[int], arr2: List[int], arr3: List[int]) -> List[int]:
i,j,k = 0,0,0
result = []
while i < (len(arr1)) and j < (len(arr2)) and k < (len(arr3)):
if arr1[i] == arr2[j] == arr3[k]:
result.append(arr1[i])
i += 1
j += 1
k += 1
elif arr1[i] < arr2[j]:
i += 1
elif arr2[j] < arr3[k]:
j += 1
else:
k += 1
if not result:
return []
return result
4. Running Sum of 1d Array - LC 1480 - Easy
class Solution:
def runningSum(self, nums: List[int]) -> List[int]:
for i in range(1, len(nums)):
nums[i] += nums[i-1]
return nums
5. Implement Merge Sort IK Problem
def merge_sort(arr):
"""
Args:
arr(list_int32)
Returns:
list_int32
"""
# Write your code here.
def helper(A, start, end):
if start >= end:
return
mid =(start + end) // 2
#divide phase
helper(A, start, mid)
helper(A, mid+1, end)
#merge phase
i = start
j = mid+1
aux = []
while i <= mid and j <= end:
if A[i] <= A[j]:
aux.append(A[i])
i += 1
else:
aux.append(A[j])
j += 1
while i <= mid:
aux.append(A[i])
i += 1
while j <= end:
aux.append(A[j])
j +=1
A[start:end+1] = aux
helper(arr, 0, len(arr)-1)
return arr
6. Two Sum - LC - 1 - Easy
Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target. You may assume that each input would have exactly one solution, and you may not use the same element twice. You can return the answer in any order
| Naive Solution | Optimized Solution | Sorted Array Solution |
|---|---|---|
|  |  |  |
| Time Complexity = O(N^2) | Time Complexity = O(N) | Time Complexity = O(NlogN) |
| Space Complexity = O(1) | Space Complexity = O(N) | Space Complexity = O(1) |
7. Maximum Subarray - LC 53 - Easy
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
if len(nums) == 1:
return nums[0]
maxSum = nums[0]
curSum = nums[0]
for i in range(1, len(nums)):
curSum = max(curSum + nums[i], nums[i])
maxSum = max(maxSum, curSum)
return maxSum
8. Remove Duplicates from sorted array - LC 26 - Easy
Approaches: Given that array is sorted, the duplicate elements can be expected to be consequtive. So the brute force or naive approach could be to traverse the array and read each element and transfer to another array if it is different from the next one.
Solution: Naive Solution: Time complexity: O(N) Space complexity: O(N)
class Naive_Solution:
def removeDups(self, nums):
temp = []
j = 0
for i in range(len(nums)-1):
if nums[i] != nums[i+1]:
temp[j] = nums[i]
j++
temp[j] = nums[i]
return j
Optimized Solution:
Time complexity: O(N)
Space complexity: O(1)
class Optimized_Solution:
def removeDups(self, nums, target):
ptr1, ptr2 = 0,0
#Initialize a variable to infinity
uniq = float('inf')
for i in range(len(nums)):
if uniq != nums[ptr2]:
uniq = nums[ptr2]
nums[ptr1] = nums[ptr2]
ptr1 += 1
ptr2 += 1
return ptr1
9. Concatenation of Array - LC 1929 - Easy
class Solution:
def getConcatenation(self, nums: List[int]) -> List[int]:
for i in range(len(nums)):
nums.append(nums[i])
return nums
10. Contains Duplicate - LC 217 - Easy
class Solution:
def containsDuplicate(self, nums: List[int]) -> bool:
seen = {}
for i in range(len(nums)):
if nums[i] in seen:
return True
seen[nums[i]] = i
return False
11. Contains Duplicate - II - LC 219 - Easy
class Solution:
def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:
seen = {}
status = False
for index, value in enumerate(nums):
if value in seen:
if (nums[seen[value]] == nums[index]) and abs(seen[value] - index) <= k:
status = True
return status
else:
seen[value] = index
status = False
else:
seen[value] = index
return status
12. Two Sum Array is Sorted - LC 167 - Medium
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
startptr = 0
endptr = len(numbers)-1
while startptr != endptr:
if numbers[startptr] + numbers[endptr] == target:
return startptr+1, endptr+1
elif numbers[startptr] + numbers[endptr] > target:
endptr -= 1
else:
startptr += 1
13. Sort the array of integers - LC 912 - Medium
Intuition:
- Analyze the best sorting algorithm candidate to do this problem.
Counting sort is used when numbers given are in narrow range. The other use case is when there are lots of duplicates and only very few unique elements. it is easy to count using counting sort.
– Two or three passes thru the array. Counting and Radix take O(n).
14. Boats to Save people - LC - 881 - Medium
class Solution:
def numRescueBoats(self, people: List[int], limit: int) -> int:
boatcnt = 0
people.sort()
leftptr = 0
rightptr = len(people) - 1
while (leftptr <= rightptr):
if leftptr == rightptr:
boatcnt += 1
break
if (people[leftptr] + people[rightptr]) <= limit:
leftptr += 1
rightptr -= 1
boatcnt += 1
else:
rightptr -= 1
boatcnt += 1
return boatcnt
15. Sort Colors or Dutch Flag Problem - LC 75 - Medium
class Solution:
def sortColors(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
r,w,b = 0,0, len(nums) - 1
while w <= b:
if int(nums[w]) == 0:
nums[w], nums[r] = nums[r], nums[w]
r += 1 # Now r points to the first white object
w += 1 # white object pointer also acts as array index.
elif int(nums[w]) == 1:
w += 1 # Since it is both array index and white pointer, just increment it
else: # If we encounter blue object
nums[w], nums[b] = nums[b], nums[w] # move it to the end
b -= 1
16. Moving Average from Data Stream - LC 346 - Easy
{{< plantuml id=‘lc346’ >}} @startjson { “Video Reference”:“Array Floater 4 Sliding Windows I : 14:14 hours”, “Notes”: " “, “Time Complexity”: “”, “Space Complexity”: "” } @endjson {{< /plantuml >}}
Code
class MovingAverage:
def __init__(self, size: int):
self.q = deque()
self.totalsofar = 0
self.size = size
def next(self, val: int) -> float:
self.totalsofar += val
self.q.append(val)
if len(self.q) > self.size:
self.totalsofar -= self.q.popleft()
return self.totalsofar / len(self.q)
Points to Note
Complexity Analysis
Coding Mistakes
17. Valid Mountain Array - 941 - Easy
Code
class Solution:
def validMountainArray(self, arr: List[int]) -> bool:
i = 0
j = len(arr) -1
if len(arr) < 2:
return False
for i in range(len(arr)-1):
if arr[i] >= arr[i+1]:
break
for j in range(len(arr)-1, 0, -1):
if arr[j-1] <= arr[j]:
break
return i == j
Points to Note:
What is a mountain array?
-
visualize the numbers as correspoinding to height/elevation. An array which has single peak (shape of conical mountain) a slope on one side steadily increasing and and slope on other side of peak steadily decreasing
-
The length is atleast 3 because we do not want the peak to be on the extreme side.
-
Can we have duplicates? Yes, on either side of the slope but not on the same side.
-
Two numbers cannot be peak.
-
Do we need to look at all the elements in the array to determine if it is mountain array or not? If yes, then we cannot use binary search approach. We have to either use two pointer or single pass of entire array.
-
Yes, we need to look at all the elements because we do not know how many peaks the array has. If we use binary search, we will be looking at the mid value and its adjacent value but it does not tell us if there is a peak in the other areas of the array.
-
Either do it in single pass by splitting into two phases. Exclusively going left to right. Or use two pointers starting at opposite extremes. The first pointer walks upto the peak and then second pointer from right walks towards left to the peak. If there is one peak, they should meet at the same point. We check at the end if the two pointers stop at the same location or not.
Edge Cases:
- If we are starting from left looking for the next element, the loop goes upto n-2. If the array is increasing all the way, the left pointer will stop at n-2 and the right pointer will stop at the rightmost index.
- If there are multiple peaks, both the left and right pointer will stop at different indices.
- If we are traversing from 0 to len() -1, then we also need to check that left and right pointers are not at the extreme.
Complexity Analysis:
- Time Complexity: \(O(N)\)
- Space Complexity: \(O(1)\)
Interval Line Sweep:
The type of problems include:
- Detect overlap?
- Measure maximum overlap?
- Merge overlapping Intervals?
- Intersection of Overlapping intervals?.
1.
Problem Statement - LC876
Video - LC876
Approaches and Thought process - LC876
-
Code - LC876
Complexity Analysis - LC876
- Time Complexity: We have to do one full traversal before we can do any validation. So the complexity is \(\color{green}{O(N)}\)
- Space Complexity: \(\color{green}{O(1)}\)
Binary Search Variants:
1. Binary Search - LC 704 - Easy
Problem Statement - LC704
Video - LC704
Code
class Solution:
def search(self, nums: List[int], target: int) -> int:
start = 0
end = len(nums) - 1
while start <= end:
mid = start + (end - start) // 2
if nums[mid] == target:
return mid
if nums[mid] < target:
start = mid + 1
else:
end = mid - 1
return -1
Points to Note
- If the collection is static, maintain the data in sorted array and do binary search
- If the collection is dynamic, (insertions and deletions are happening), keep the data in tree or hash table
- Python has native function to do binary search
def search(nums, target):
i = bisect.bisect_left(nums, target)
if i == len(nums) or nums[i] != target:
return -1
else:
return i
- General info: If we take all the atoms in the universe and take their log then:
\begin{equation} \log_2(10^{80}) < 300 \end{equation}
- This means that it does not require more than 300 iterations to cover entire atoms in the universe. This is the power of log.
- An algo that runs in log N time is almost like constant time…for all practical purposes.
Why not have Ternary search instead of binary search? Would this further reduce the time complexity?
- Have two mids and check the target against each mids.
- After each round, the size reduces factor of 3.
- So on ith round we get \(\log_3 n\)
- Compared to binary search \(\log_2 n\), there is only constant factor of difference.
- In binary search, we make two comparisions in every step
- there are \(\log_2n\) steps so at max we make \(2 * \log_2 n\) comparisions
- In ternary search, we make 4 comparisions per step
- There are \(\log_3 n\) steps so we make max \(4 * \log_3 n\) comparisions
- Between \(2\log_2 n\) and \(4\log_3 n\), which one is bigger?
- We can look at the ratio of these and if the ratio is more than 1, numerator is bigger else denominator is bigger.
\[\begin{eqnarray} \frac{4 \log_3 n}{2 \log_2 n} = ? \nonumber \\ \log_3 n = \frac{\log n}{log 3} \text {log n can be of any base} \nonumber \\ \text{similarly} \log_2 n = \frac{\log n}{log 2} \nonumber \\ \frac{4 \log_3 n}{2 \log_2 n} = \frac{2 \log n * \log 2}{\log 3 * \log n} \nonumber \\ &=& \frac{2 * \log 2}{\log 3} &=& \boxed{\sim 1.26} \end{eqnarray}\]
This shows that ternary search costs more than binary search.
On space complexity, in ternary search, the height of the tree is smaller than binary search but not exactly half but the amount of work done in ternary search is lot more which is why it is not preferred.
Complexity Analysis
Time Complexity
Q. How many iterations it takes for binary search to size 1? Assuming we start with a range of n,
\[\begin{eqnarray} \text{Assume the range of input array} &=& n \nonumber \\ \text{After first round} &=& n/2 \nonumber \\ \text{After second round} &=& \frac{n}{2^2} \nonumber \\ \text{After third round} &=& \frac{n}{2^3} \nonumber \\ \text{After ith round} &=& \frac{n}{2^i} \nonumber \\ \text{Equating} \frac{n}{2^i} &=& 1 \nonumber \\ 2^i = n \nonumber \\ \boxed{\therefore{ i } = \log_2 n} \end{eqnarray}\]
Space Complexity \[\begin{eqnarray} \text{For Iterative Code} &=& O(1) \nonumber \\ \text{For Recursive Code} &=& O(\log_2 n) \nonumber \\ \end{eqnarray}\]
Hence iterative code is mostly preferred for binary search.
2. Guess the Number - LC 374 - Easy
Problem Statement - LC374
Video - LC374
Code
3. First Bad Version - LC 278 - Easy
Problem Statement - LC278
Video - LC278
Code
# The isBadVersion API is already defined for you.
# def isBadVersion(version: int) -> bool:
class Solution:
def firstBadVersion(self, n: int) -> int:
start = 1
end = n
while start <= end:
mid = start + (end - start) // 2
bad_version = isBadVersion(mid)
if bad_version:
end = mid - 1
else:
start = mid + 1
return start
Points to Note
-
In this problem, we do not check for any target. Typically there are three checks in the loop and the checking ofr target is not needed for this problem.
-
In binary search, if we let the while loop run
start <= endat the end of the loop, start moves one step right of the boundary and end moves one step left of boundary. (whichever boundary we select…in this case, it is the mid) -
The behavior of start and end at the end of binary search loop is a interesting behavior to keep in mind for many kinds of problems including this.
-
When binary search for x ends unsuccessfully,
- start = end + 1
- End points to the largest number < x
- Start points to the smallest number > x
Complexity Analysis
4. Search Insert Position - LC 35 - Easy
Problem Statement - LC35
Video - LC35
Code
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
start = 0
end = len(nums) - 1
while start <= end:
mid = start + (end - start) // 2
if nums[mid] == target:
return mid
if nums[mid] < target:
start = mid + 1
else:
end = mid - 1
return start
Points to Note
Complexity Analysis
- Time Complexity = \(\log_2 N\)
- Space Compleixty = \(O(1)\)
5. Find smallest letter greater than target - LC 744 - Easy
Problem Statement - LC744
Code
class Solution:
def nextGreatestLetter(self, letters: List[str], target: str) -> str:
start = 0
end = len(letters) - 1
while start <= end:
mid = start + (end - start) // 2
if letters[mid] <= target:
start = mid + 1
else:
end = mid - 1
return letters[start % len(letters)]
Points to Note
Complexity Analysis - LC744
- Time Complexity = \(\log_2 N\)
- Space Compleixty = \(O(1)\)
6. Search in a sorted array of unknown size - 702 - Medium
Problem Statement - LC702
Video - LC702
Code
class Solution:
def search(self, reader: 'ArrayReader', target: int) -> int:
end = 1
while reader.get(end) < target:
end *= 2
start = end // 2
while start <= end:
mid = start + (end - start) // 2
val = reader.get(mid)
if val == target:
return mid
if val < target:
start = mid + 1
else:
end = mid - 1
return -1
Points to Note
-
This is the same binary search problem since the time complexity expected is \(O(\log_2 N)\). However, the array length of the last index is not given. Array cannot be accessed directly other than using an API.
-
If we try to find the length of the array, it becomes \(O(N)\).
-
We have to be very careful about how to interpret the problem. The problem constraints may have limited values of the array..but they are not talking about the index or length. The array may have duplicates which increases the size
-
One suggestion was to use the MAX(INT) as the array size… if the array is actually smaller than this, then we would be spending lot more time to process the array than it is necessary.
-
The key thing here is how quickly to traverse the array and one option is to start going in multiple of 2. Initialize the end pointer to 1 and multiply it by 2 and call the API to check if it is less than target and continue this until the condition fails. The condition will fail with the first garbage value that is greater than the target or end of array.
-
At this point, initialize the start pointer to half of end pointer and use this range for the standard binary search for the target.
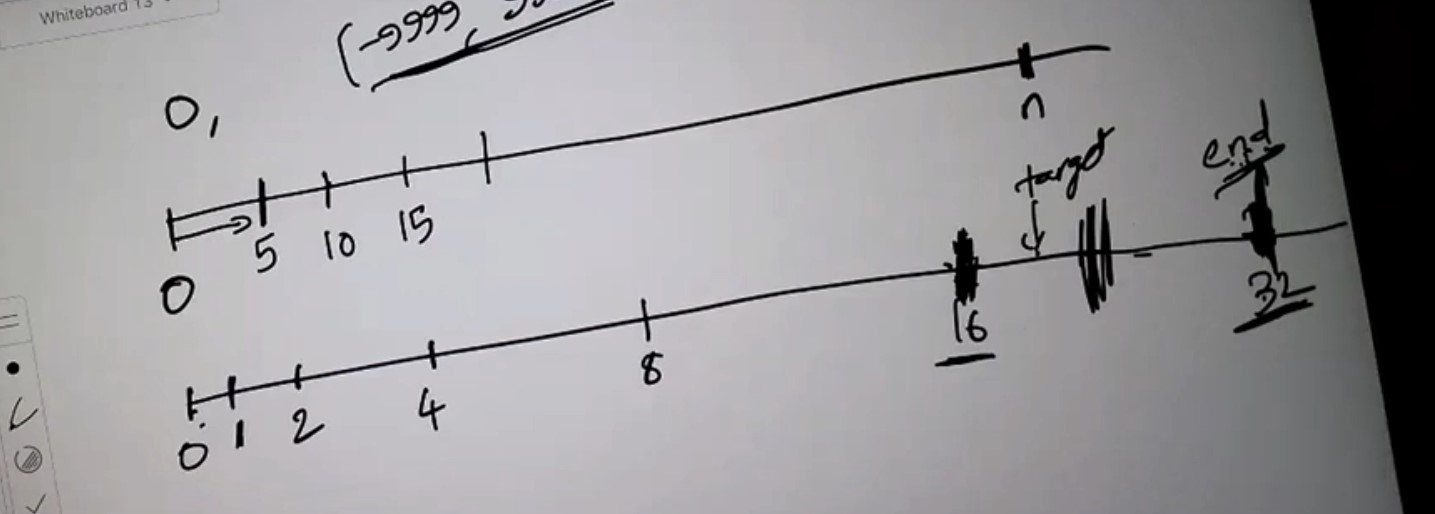
- One logical question that may come up is why not then multiply by 3 instead of 2 to speed up the array traversal to find the end of array. Yes, but it is a constant difference between \(\log_2N\) multiplication operations and \(\log_3N\) multiplication operations. Moreover, the range is higher if we decide to go with multiplying with 3.
Complexity:
- Time Complexity: \(O(\log_2N)\)
- Space Complexity: \(O(1)\)
7. Peak index in a mountain array - 852 - Easy
Problem Statement - LC852
Video
Code
class Solution:
def peakIndexInMountainArray(self, arr: List[int]) -> int:
start = 1
end = len(arr) - 2
while start <= end:
mid = start + (end-start)//2
# The additional checks to ensure peak is not at the either end.
#Another way is to start from 1st index instead of 0.
#if arr[mid -1} < arr[mid] > arr[mid+1] and mid != 0 and mid != len(arr) - 1:
if arr[mid-1] < arr[mid] > arr[mid+1]:
return mid
elif arr[mid] > arr[mid -1]:
start = mid + 1
else:
end = mid - 1
Points to Note:
-
Given the problem array is a mountain array, it structure is such that in the interior, it is going to have a peak and the left of it will be ascending zone and right of it is descending zone.
-
If we start from -0th index and go all the way to len(array) - 1: then we need explicit check to see peak is not in the extremes. Omkar said this is a corner case and there could be mountain arrays with peak at the extremes.
Complexity Analysis:
- Time Complexity: \(O(\log_2N)\)
- Space Complexity: \(O(1)\)
Cycle Sort Variants:
1. Missing Number - LC 268 - Easy
- Video Reference: Array Floater 1 - Cycle Sort - 1:46:45
Code
class Solution:
def missingNumber(self, nums: List[int]) -> int:
# Pigeon hole principle
n = len(nums)
for i in range(n):
while nums[i] != i: #The value and index should match, swap values until they match
d = nums[i]
if d < n: # Swap only if the value is not spurious
nums[i], nums[d] = nums[d], nums[i]
else:
break
for i in range(n):
if nums[i] != i:
return i
return n
Points to Note
Complexity Analysis
- Time Complexity = \(O(N)\)
- Space Compleixty = \(O(1)\)
2. Find All numbers disappeared in an array - LC 448 - Easy
- Video Reference: Array Floater 1 - Cycle Sort - 3:16:30
Code
class Solution:
def findDisappearedNumbers(self, nums: List[int]) -> List[int]:
result = []
for i in range(len(nums)):
while nums[i] != i + 1:
d = nums[i] - 1
if nums[d] != nums[i]:
nums[i], nums[d] = nums[d], nums[i]
else:
break
for i in range(len(nums)):
if nums[i] != i + 1:
result.append(i+1)
return result
Points to Note
Complexity Analysis
- Time Complexity = \(O(N)\)
- Space Compleixty = \(O(1)\)
3. Find the duplicate number - LC 287 - Easy
- Video Reference: Array Floater 1 - Cycle Sort - 3:39:45
Code
class Solution:
def findDuplicate(self, nums: List[int]) -> int:
for i in range(len(nums)):
while nums[i] != i:
d = nums[i]
if nums[d] != nums[i]:
nums[d], nums[i] = nums[i], nums[d]
else:
break
return nums[0]
Points to Note
at 3:59 hours, Omkar tablks about solving it using bitwise operator videos. Check with IK.
Complexity Analysis
- Time Complexity = \(O(N)\)
- Space Compleixty = \(O(1)\)
4. Set Mismatch - LC 645 - Easy
- Video Reference: Array Floater 1 - Cycle Sort - 4:16:06
Code
class Solution:
def findErrorNums(self, nums: List[int]) -> List[int]:
for i in range(len(nums)):
while nums[i] != i + 1:
d = nums[i] - 1
if nums[d] != nums[i]:
nums[d], nums[i] = nums[i], nums[d]
else:
break
for i in range(len(nums)):
if nums[i] != i + 1:
return [nums[i], i+1]
Points to Note
Analysis
- Time Complexity = \(O(N)\)
- Space Compleixty = \(O(1)\)
5. Find all duplicates in an array - 442 - Easy
- Video Reference: Array Floater 1 - Cycle Sort - 4:16:06
Code
class Solution:
def findDuplicates(self, nums: List[int]) -> List[int]:
for i in range(len(nums)):
while nums[i] != i + 1:
d = nums[i] - 1
if nums[d] != nums[i]:
nums[d], nums[i] = nums[i], nums[d]
else:
break
result = []
for i in range(len(nums)):
if nums[i] != i+1:
result.append(nums[i])
return result
Points to Note
Analysis
- Time Complexity = \(O(N)\)
- Space Compleixty = \(O(1)\)
7. Find first and last position of element in sorted array - 34 - Medium
- Video Reference: Array Floater 5 - Sliding Window II - 0:29:00 hrs
Code
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
start = 0
end = len(nums) - 1
while start <= end:
mid = start + (end - start) // 2
if nums[mid] < target:
start = mid + 1
else:
end = mid - 1
if start > len(nums)-1 or nums[start] != target:
return [-1,-1]
first = start
end = len(nums) - 1
while start <= end:
mid = start + (end - start) // 2
if nums[mid] > target:
end = mid - 1
else:
start = mid + 1
return [first, end]
Points to Note
8. Check if a number is majority element in a sorted array - 1150 - Easy
Problem Statement - LC1150
Video - LC1150
Code
class Solution:
def isMajorityElement(self, nums: List[int], target: int) -> bool:
start = 0
end = len(nums) - 1
while start <= end:
mid = start + (end - start) // 2
if nums[mid] < target:
start = mid + 1
else:
end = mid - 1
if start == len(nums) or nums[start] != target:
return False
first = start
end = len(nums) - 1
while start <= end:
mid = start + (end - start) // 2
if nums[mid] > target:
end = mid - 1
else:
start = mid + 1
if end - first + 1 > len(nums) // 2:
return True
return False
class Solution:
def isMajorityElement(self, nums: List[int], target: int) -> bool:
start = 0
end = len(nums) - 1
while start <= end:
mid = start + (end - start) // 2
if nums[mid] < target:
start = mid + 1
else:
end = mid - 1
if start == len(nums) or nums[start] != target:
return False
end = start + (len(nums) // 2)
if end < len(nums) and nums[end] == target:
return True
return False
Points to Note
9. Search 2D matrix - 74 - Medium
- Video Reference: Array Floater 5 - Sliding Window II - 0:29:00 hrs
Code
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
if len(matrix) == 0:
return False
start = 0
end = len(matrix) * len(matrix[0]) - 1
n = len(matrix[0])
while start <= end:
mid = start + (end - start) // 2
if matrix[mid // n][mid % n] == target:
return True
if matrix[mid // n][mid % n] < target:
start = mid + 1
else:
end = mid - 1
return False
Points to Note
Prefix Sum Problems:
1.
{{< video src="/IK/arrays/lc325.mp4" controls=“yes” >}}
Sliding Window - Fixed Length:
1. Moving Average from Data Stream - LC 346 - Easy
Code
class MovingAverage:
def __init__(self, size: int):
self.win = size
self.val = 0
self.q = deque()
def next(self, val: int) -> float:
self.val += val
self.q.append(val)
if len(self.q) > self.win:
lastval = self.q.popleft()
self.val -= lastval
return self.val / len(self.q)
# Your MovingAverage object will be instantiated and called as such:
# obj = MovingAverage(size)
# param_1 = obj.next(val)
Points to Note
Complexity Analysis
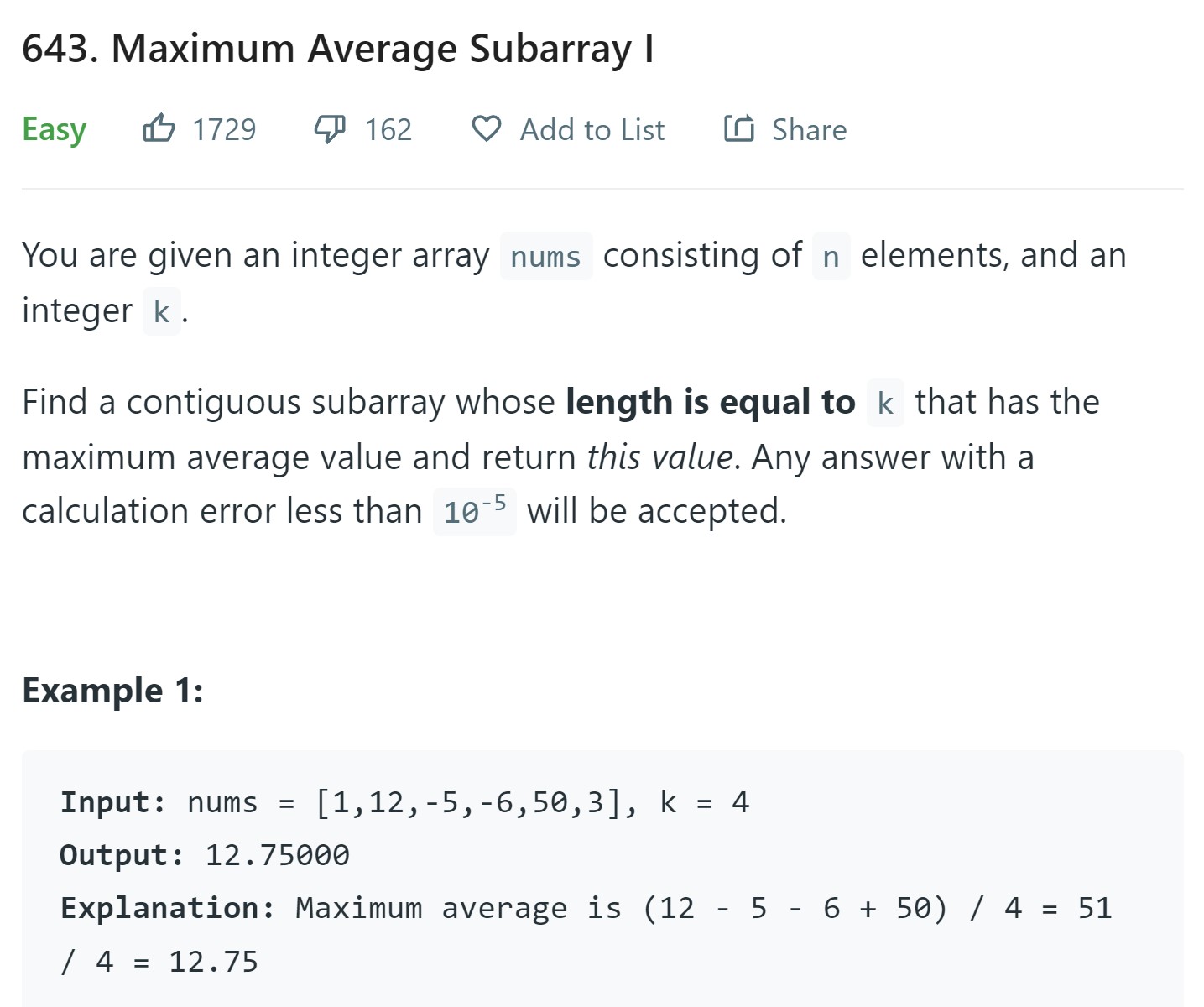
2. Maximum Average Subarray I - 643 - Easy
Code
class Solution:
def findMaxAverage(self, nums: List[int], k: int) -> float:
window_sum = sum(nums[:k])
maxsum = window_sum
for i in range(k, len(nums)):
window_sum += nums[i] - nums[i-k]
maxsum = max(maxsum, window_sum)
return float(maxsum) / k
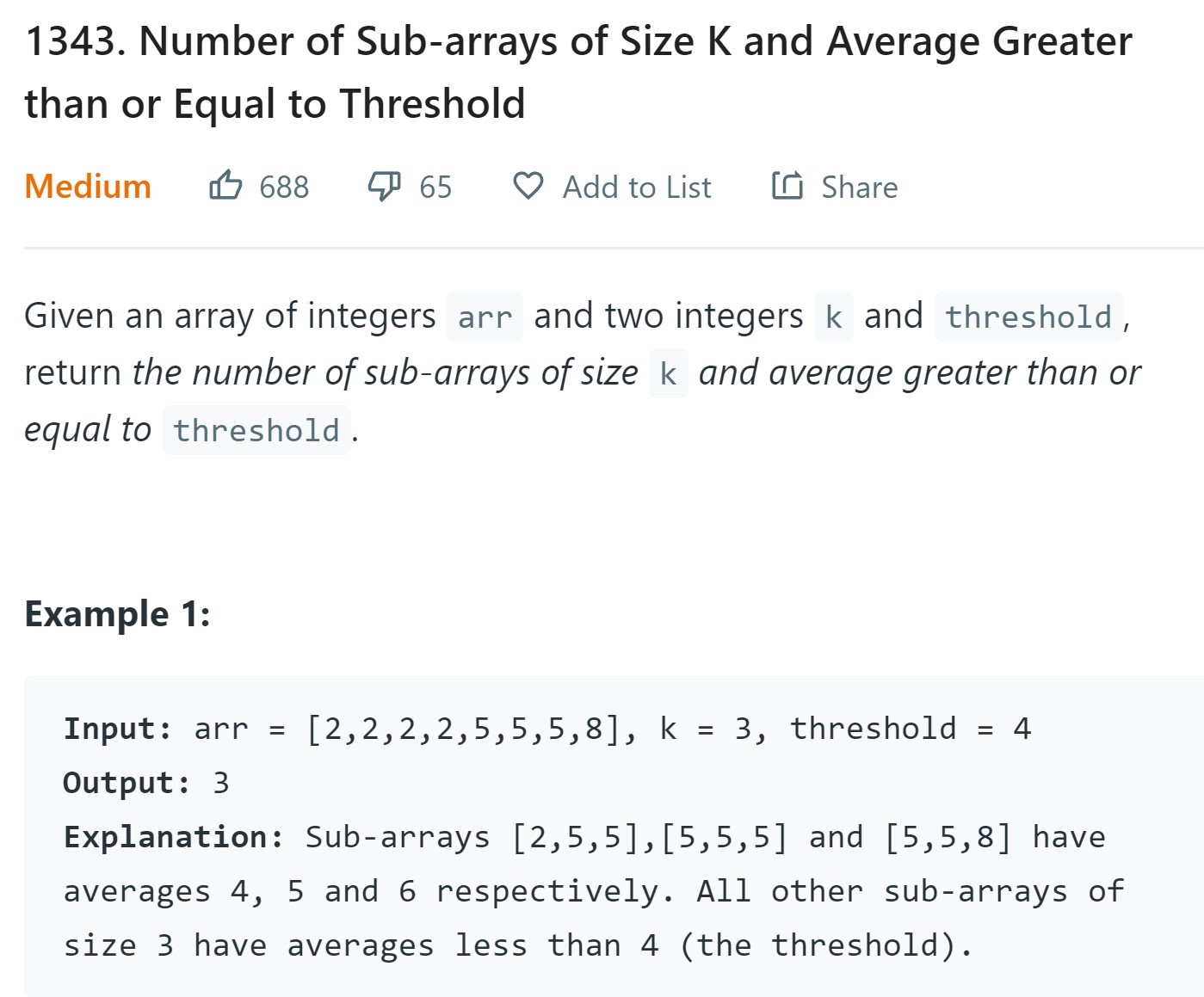
3. Number of Subarrays of size K and average greater than or equal to threshold - 1343 - Medium
Code
class Solution:
def numOfSubarrays(self, arr: List[int], k: int, threshold: int) -> int:
avg = threshold * k
window_sum = sum(arr[:k])
if window_sum >= avg:
subarray_count = 1
else:
subarray_count = 0
for i in range(k, len(arr)):
window_sum += arr[i] - arr[i-k]
if window_sum >= avg:
subarray_count += 1
return subarray_count
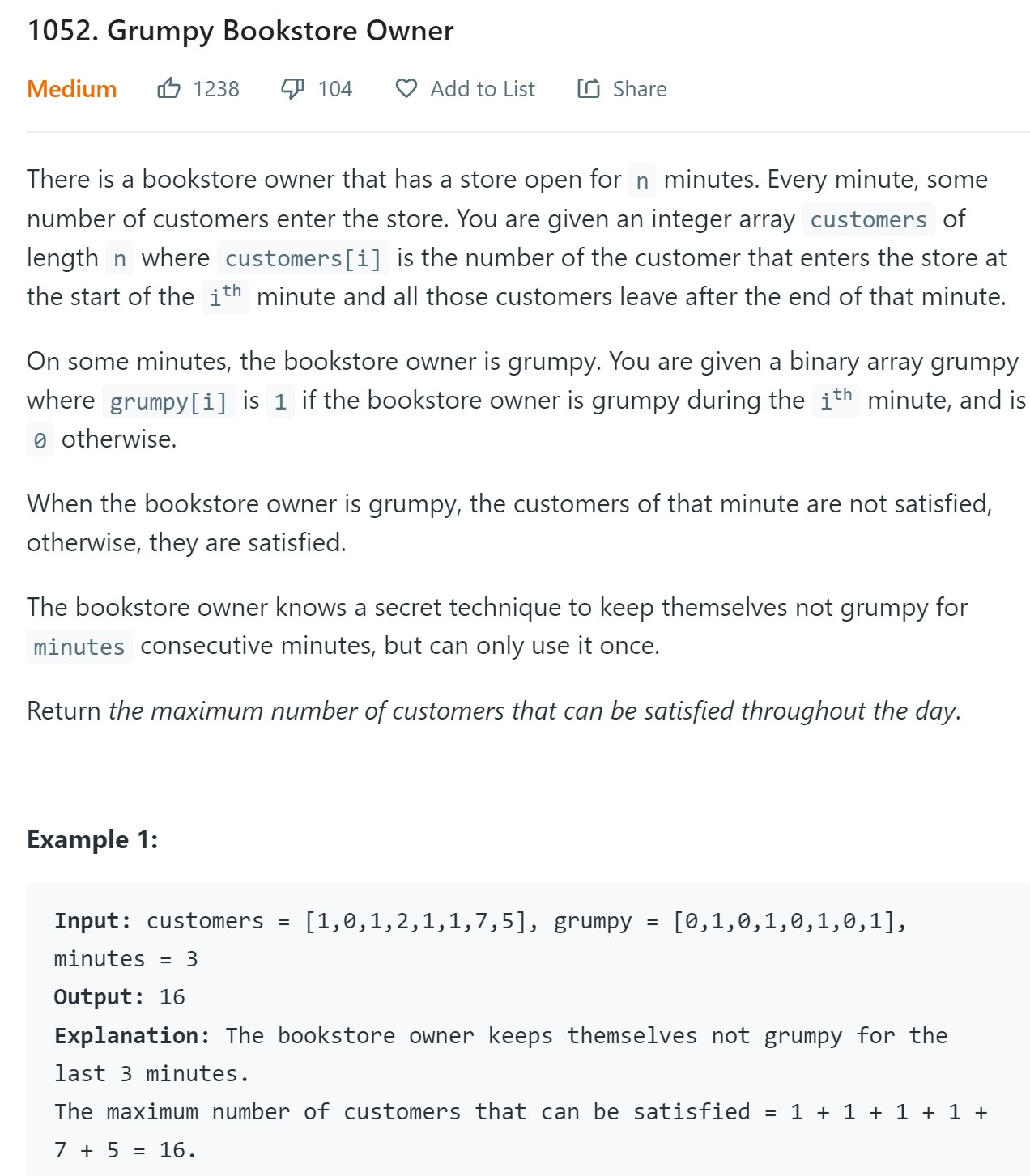
4. Grumpy Book Store Owner - 1052 - Medium
Code
class Solution:
def maxSatisfied(self, customers: List[int], grumpy: List[int], minutes: int) -> int:
#Initialization
numangry = 0
satisfied = 0
for i in range(minutes):
if grumpy[i] == 1:
numangry += customers[i]
for i in range(len(customers)):
if grumpy[i] == 0:
satisfied += customers[i]
maxunhappy = numangry
# Main loop
for i in range(minutes, len(customers)):
# Check the ith element
if grumpy[i] == 1:
numangry += customers[i]
# Remove the oldest one from the window
if grumpy[i-minutes] == 1:
numangry -= customers[i-minutes]
maxunhappy = max(maxunhappy, numangry)
return satisfied + maxunhappy
Sliding Window - Variable Length
4. Longest Substring without repeating characters - LC 3 - Medium
Code
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
maxlen = 0
left = 0
hmap = {}
for i in range(len(s)):
if s[i] in hmap:
hmap[s[i]] += 1
else:
hmap[s[i]] = 1
while left <= i and hmap[s[i]] > 1:
hmap[s[left]] -= 1
if hmap[s[left]] == 0:
del hmap[s[left]]
left += 1
maxlen = max(maxlen, i - left + 1)
return maxlen
5. Longest Substring with at most k distinct characters - LC 340 - Medium
Code
class Solution:
def lengthOfLongestSubstringKDistinct(self, s: str, k: int) -> int:
hmap = {}
left = 0
maxlen = 0
for i in range(len(s)):
if s[i] in hmap:
hmap[s[i]] += 1
else:
hmap[s[i]] = 1
while left <= i and len(hmap) > k:
hmap[s[left]] -= 1
if hmap[s[left]] == 0:
del hmap[s[left]]
left += 1
maxlen = max(maxlen, i-left + 1)
return maxlen
6. Longest Substring with at most two distinct characters - LC 159 - Medium
Code
class Solution:
def lengthOfLongestSubstringTwoDistinct(self, s: str) -> int:
hmap = {}
left = 0
maxlen = 0
for i in range(len(s)):
if s[i] in hmap:
hmap[s[i]] += 1
else:
hmap[s[i]] = 1
while left <= i and len(hmap) > 2:
hmap[s[left]] -= 1
if hmap[s[left]] == 0:
del hmap[s[left]]
left += 1
maxlen = max(maxlen, i - left + 1)
return maxlen
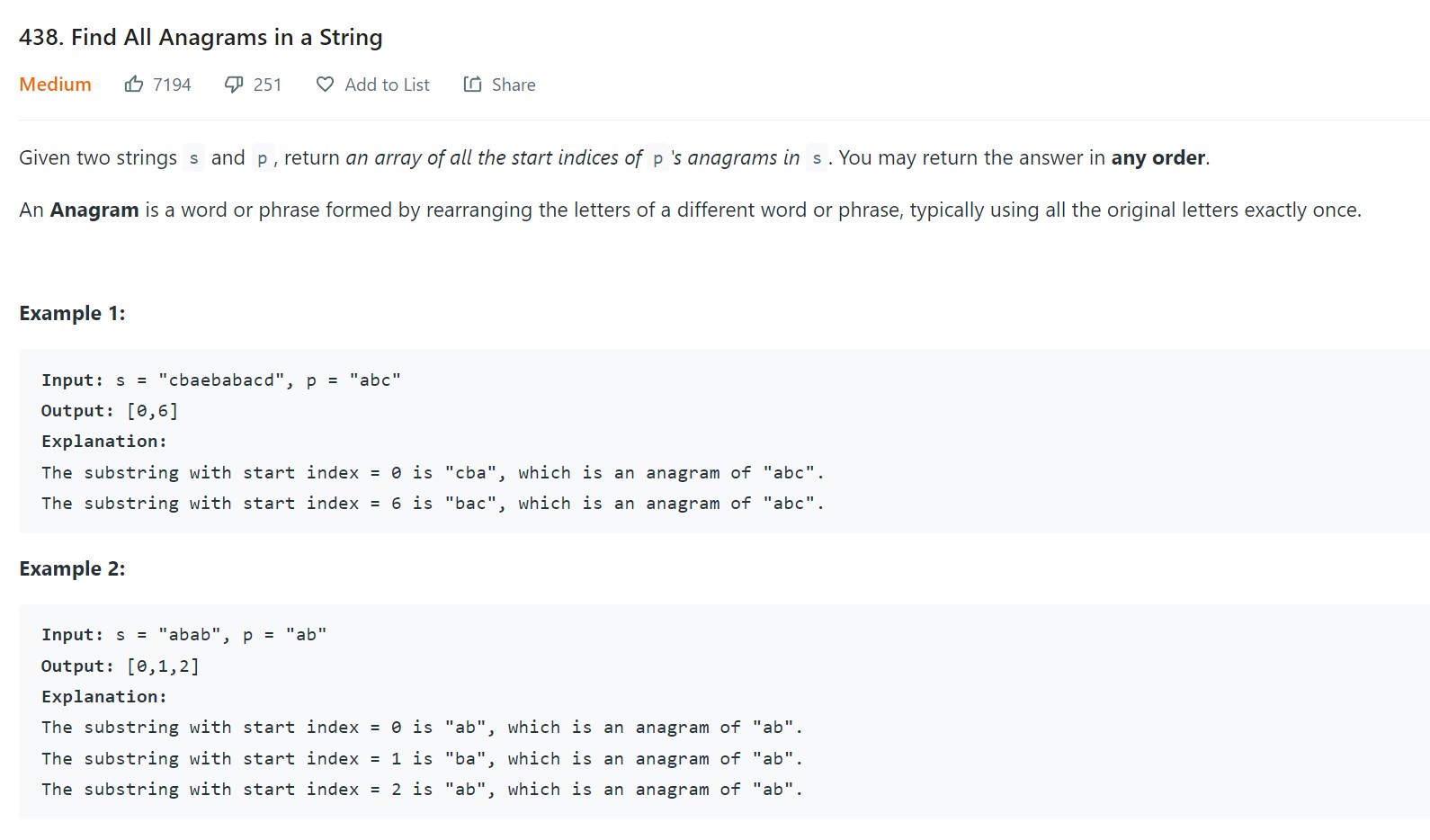
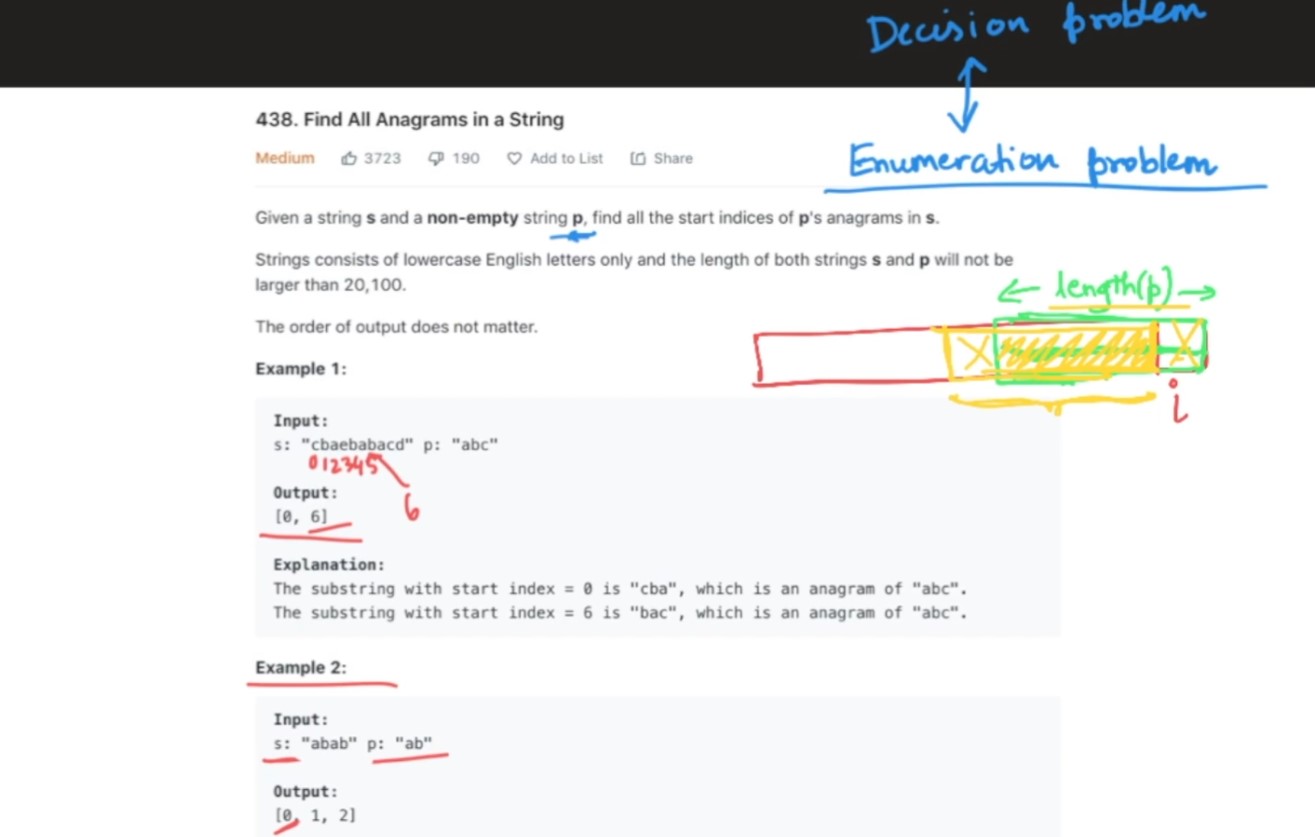
7. Find all Anagrams in a string - 438 - Medium
Problem Statement - LC438
Video - LC438
Code
class Solution:
def findAnagrams(self, s: str, p: str) -> List[int]:
result = []
if len(p) > len(s):
return result
#Initialize hmap_p
k = len(p)
hmap_p = {}
for i in range(k):
if p[i] in hmap_p:
hmap_p[p[i]] += 1
else:
hmap_p[p[i]] = 1
#Initialize sliding window
hmap_s = {}
for i in range(k):
if s[i] in hmap_s:
hmap_s[s[i]] += 1
else:
hmap_s[s[i]] = 1
if hmap_s == hmap_p:
result.append(0)
for i in range(k, len(s)):
if s[i] in hmap_s:
hmap_s[s[i]] += 1
else:
hmap_s[s[i]] = 1
hmap_s[s[i-k]] -= 1
if hmap_s[s[i-k]] == 0:
del hmap_s[s[i-k]]
if hmap_s == hmap_p:
result.append(i-k+1)
return result
Points to Note
- This is enumeration problem. Enumeration all instances, instead of
copying the enumeration, record the index where it occurs. In the
Permutations of stringproblem, it was decision problem of returning True or False.
Brute Force Approach:
-
Generate all permutations of string P and look for presence of each permutation anywhere inside string S and see where all it occurs and record the index and do the same with other permutation. This is exhaustive way.
-
Since we do not need to worry about order of the occurence of letter, convert p into frequency table and for each location of S, create a frequency table of length p in that substring and compare.
Fixed Sliding Window:
- With decrease and conquer, a manager would bother only with the index i. Let us say a subarray ends in index i with length equal to length of P and we want to check if this subarray matches frequency table of P.
- Since subordinates will also be doing this work, a frequency table would be already available and we inherit it and eliminate left most charactera and add rightmost character. Thus, entire frequency table need not be constructed from scratch and ends up with fixed length sliding window problem where the length of window is length of string p.
- Thus frequency table can be updated in constant time and not of length proportional to p.
Complexity
8. Subarray product less than K - 713 - Medium
Problem Statement - LC713
Video - LC713
Code
class Solution:
def numSubarrayProductLessThanK(self, nums: List[int], k: int) -> int:
window_product = 1
global_answer = 0
left = 0
for i in range(len(nums)):
window_product = window_product * nums[i]
while left <= i and window_product >= k:
window_product = window_product / nums[left]
left += 1
global_answer += i - left + 1
return global_answer
Points to Note
Option 1: Brute Force by Exhaustive enumeration
-
For a given array, there are O(N^2) subarrays. Computing products for a subarray will take O(N) So for O(N^2) subarrays, the total worst case complexity will be O(N^3) or cubic time complexity if done in naive way.
-
Similar to prefix sum, we could keep prefix products to speed up computation of products of all elements within a subarray from index i to index j.
-
To compute prefix products of i to j elements:
- Calculate prefix products all the way to j
- Subtract prefix products from 0 to i-1
-
Though prefix product computation has constant time, given O(N^2) subarrays, this will take O(N^2) time/quadratic time. This is variable length sliding window.
Complexity
- Time complexity is O(N)
- Space Complexity is O(1)
IK Problem Set
- Sorting Class Problems
- Sorting Algorithms Practice - New Problem Set 1
- Sorting Algorithms Practice Problem Set 2
9. Minimum Operations to Reduce X to Zero - 1658 - Medium
Problem Statement - LC1658

Video - LC1658
Code
class Solution:
def minOperations(self, nums: List[int], x: int) -> int:
left = 0
globalmax = -1
windowsum = 0
k = sum(nums) - x
for i in range(len(nums)):
windowsum += nums[i]
while left <= i and windowsum > k:
windowsum -= nums[left]
left += 1
if windowsum == k:
globalmax = max(globalmax, i-left+1)
if globalmax == -1:
return -1
return len(nums) - globalmax
Unclassified:
1. Majority Element - 169 - Easy

Clarification Questions
- Data type: “Can I assume the array contains only integers?”
- Array size: “Are there any constraints on the size of the array?”
- Example: “Could you provide an example to illustrate the expected output?”
- Sorted array: “Is the array sorted?”
Thought Process
- Brute Force: Iterate through the array, and for each element, count its occurrences. If the count exceeds n / 2, you’ve found the majority element.
- Hashmap approach: Use a HashMap to store each element and its count. This avoids nested loops and improves performance.
- Bayer Moore Algorithm: The Boyer-Moore Voting Algorithm is a clever way to find the majority element in an array—that is, the element that appears more than half the time. It leverages the fact that the majority element appears more than half the time.

Code
# Brute Force Approach:
def majorityElement(nums):
n = len(nums)
for i in range(n):
count = 0
for j in range(n):
if nums[i] == nums[j]:
count += 1
if count > n // 2:
return nums[i]
# Hashmap Approach:
def majorityElement(nums):
counts = {}
for num in nums:
counts[num] = counts.get(num, 0) + 1
if counts[num] > len(nums) // 2:
return num
# Bayer Moore Algorithm
def majorityElement(nums):
candidate = nums[0]
count = 1
for num in nums[1:]:
if num == candidate:
count += 1
else:
count -= 1
if count == 0:
candidate = num
count = 1
return candidate
Complexity:
- Brute force Approach:
- Time Complexity: \(O(N^2)\)
- Space complexity: \(O(1)\)
- Hash Map Approach:
- Time Complexity: \(O(N)\)
- Space complexity: \(O(N)\)
- Bayer Moore Approach:
- Time Complexity: \(O(N)\)
- Space complexity: \(O(1)\)
Test Cases
def test_majority_element():
assert majorityElement([3, 2, 3]) == 3 # Basic case
assert majorityElement([2, 2, 1, 1, 1, 2, 2]) == 2 # Example from explanation
assert majorityElement([1]) == 1 # Single element
assert majorityElement([1, 1, 1, 2, 2, 2, 2]) == 2 # Majority at the end
assert majorityElement([4, 4, 2, 3, 4, 4, 4]) == 4 # Majority with other elements
IK Problem Set