Dynamic Programming Problems
- Problems
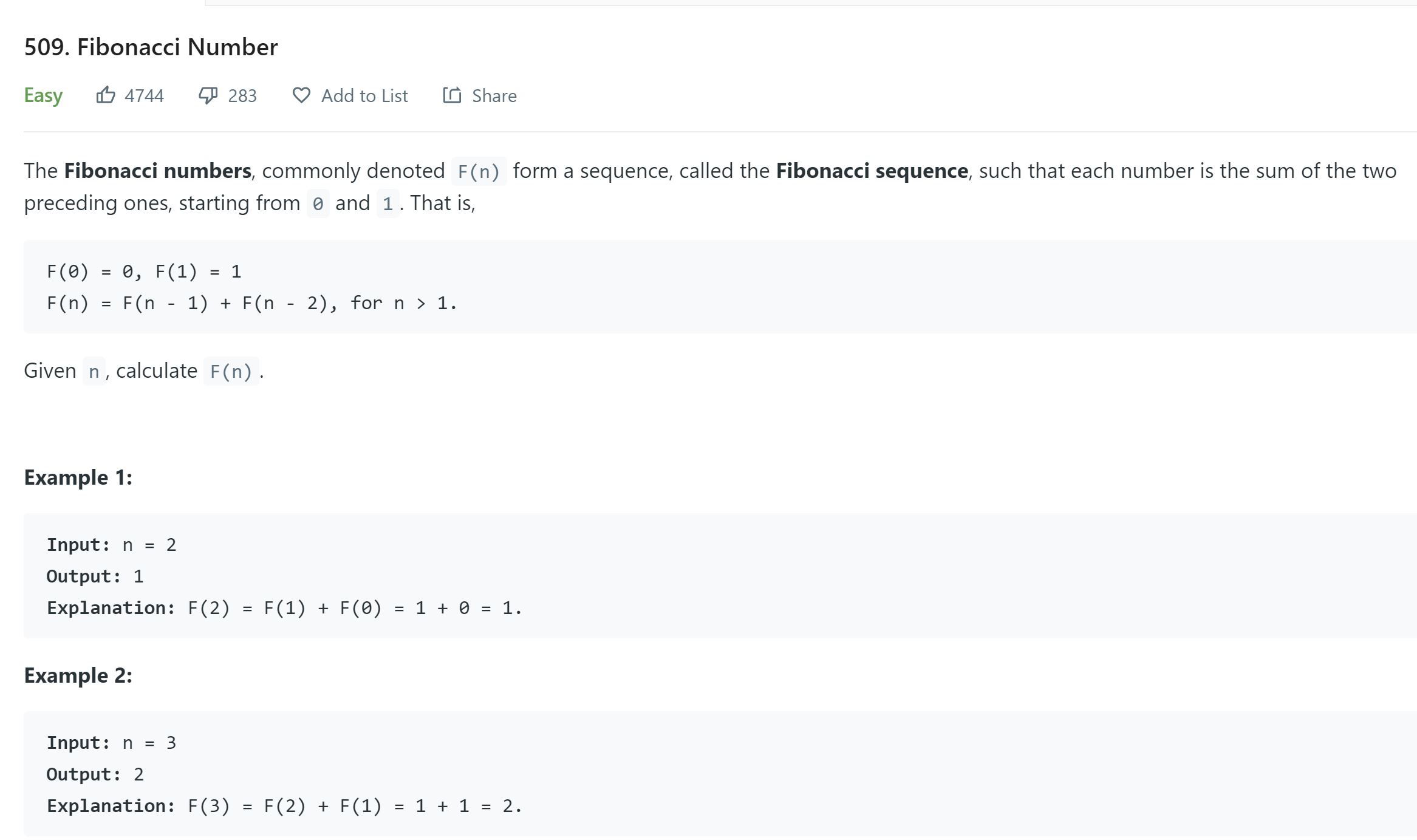
- 1. Fibonacci Number - 509 - Easy
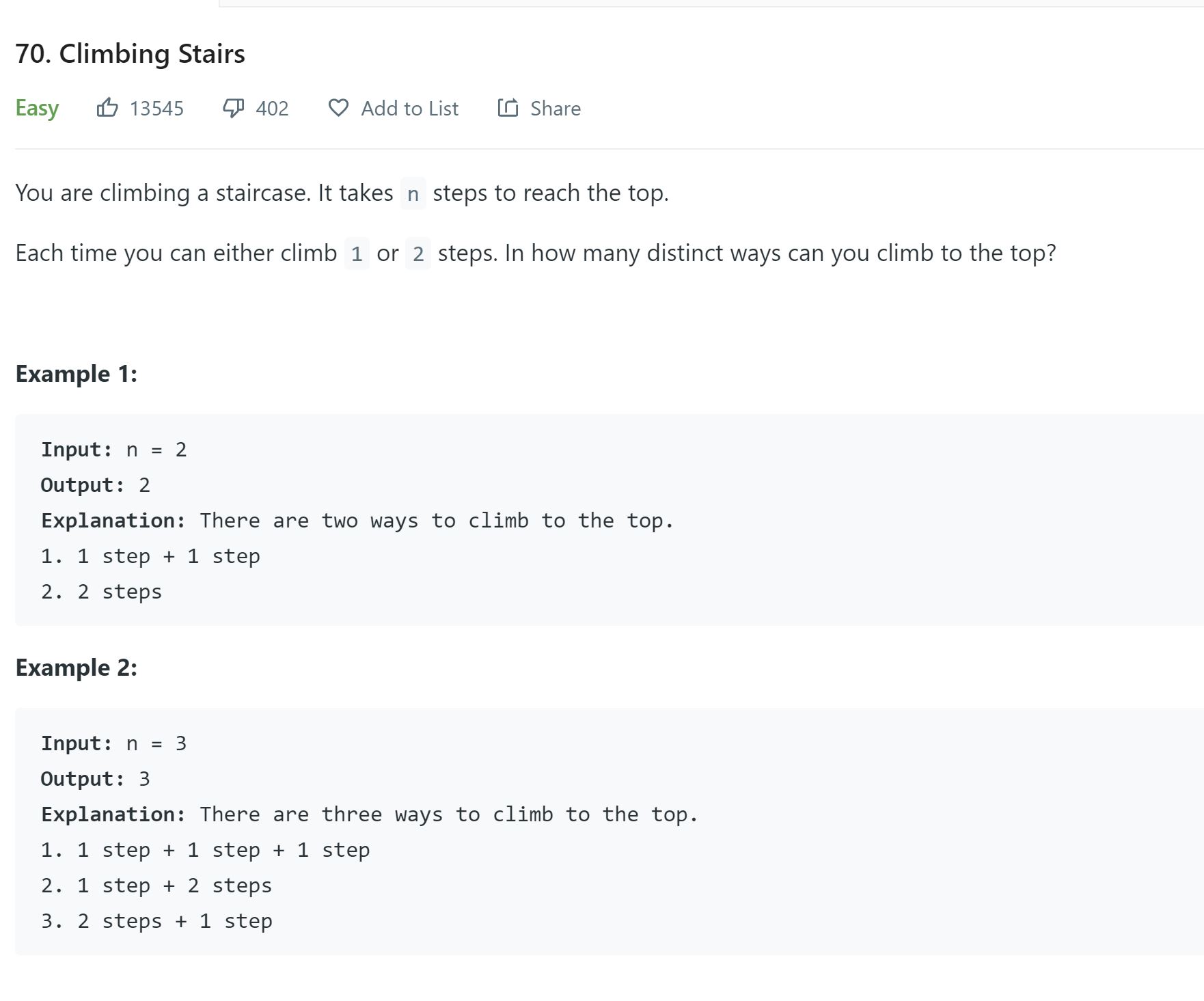
- 2. Number of ways of climing stairs - 70 -Easy
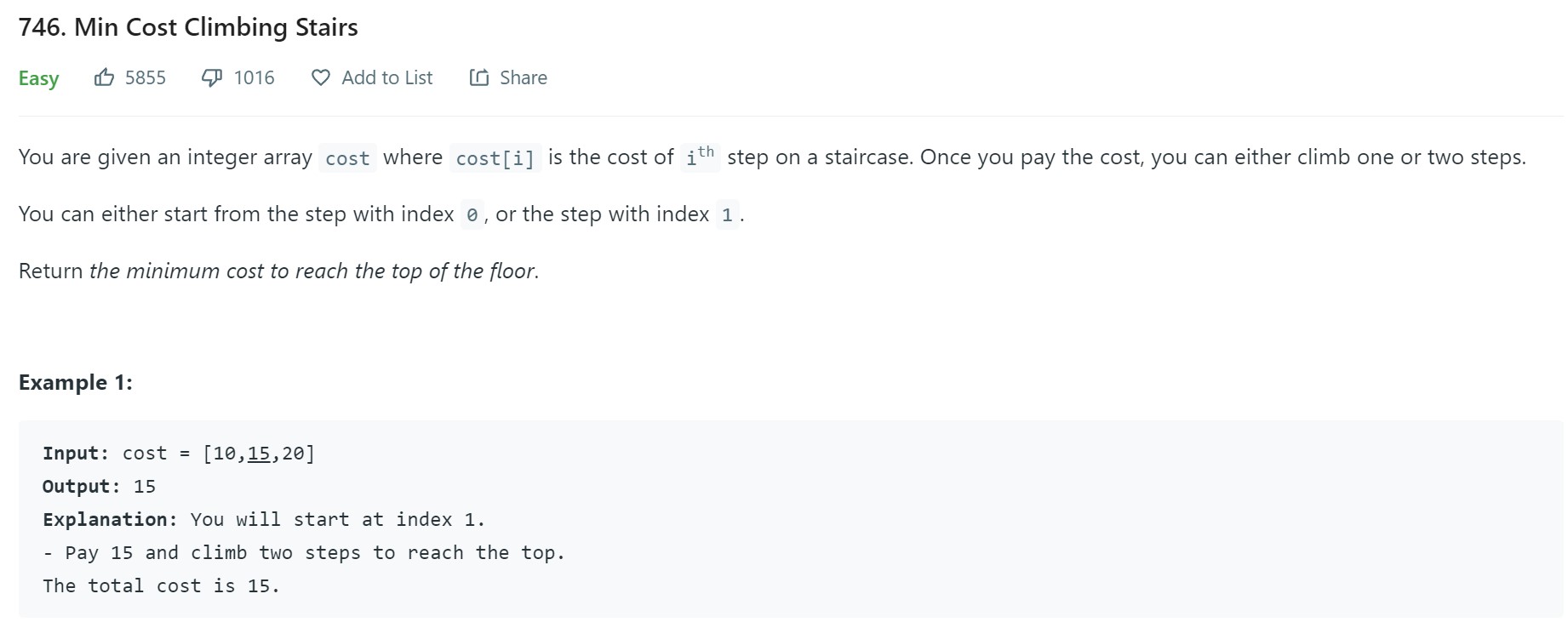
- 3: Minimum Cost of Climbing Stairs - 746 - Easy
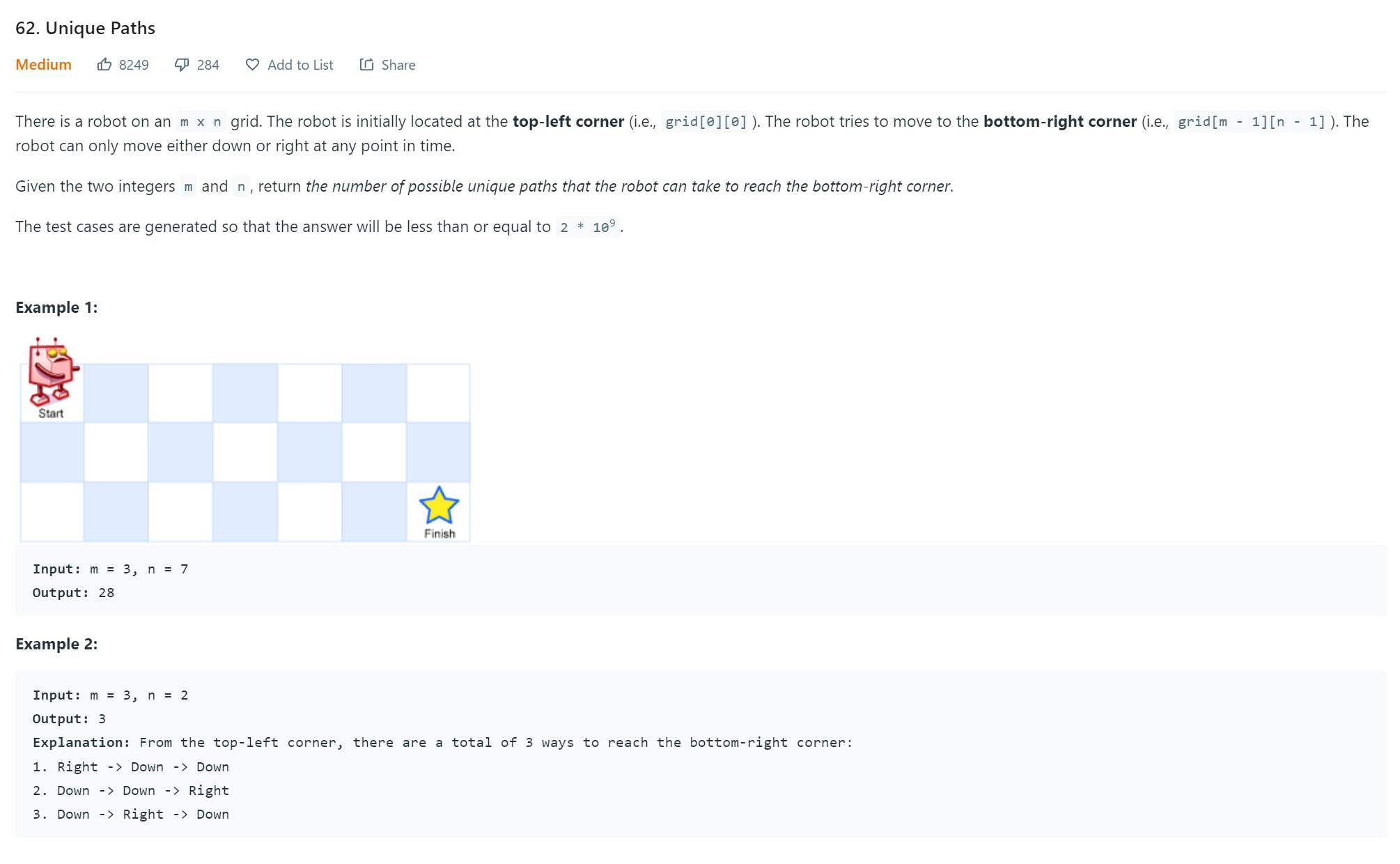
- 4. Unique Paths - LC 62 - Easy
- 5. Unique Paths II - LC 63 - Medium
- 6. House Robber - LC 198 - Medium
- 7. House Robber II - LC 213 - Medium
- 8. Paint house - 256 - Medium
- 9. Pascal’s Triangle - 118 - Easy
- 10. Triangle - 120 - Medium
- 11. Combination Sum IV - 377 - Medium
- 12. Paint House II - 265 - Hard
- 13. Edit Distance - 72 - Hard
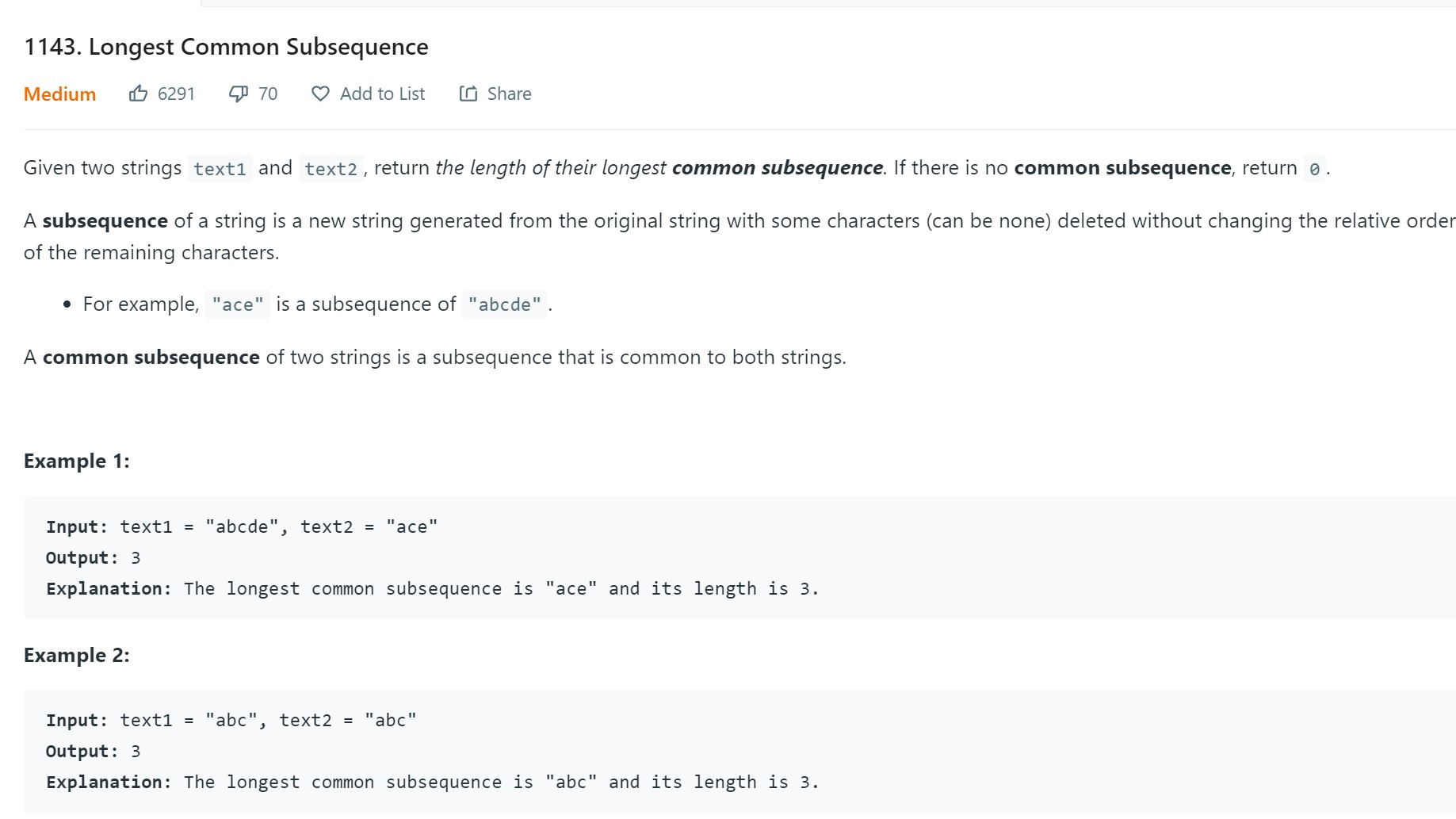
- 14. Longest Common Subsequence - 1143 - Medium
- 15. Delete Operations for two strings - 583 - Medium
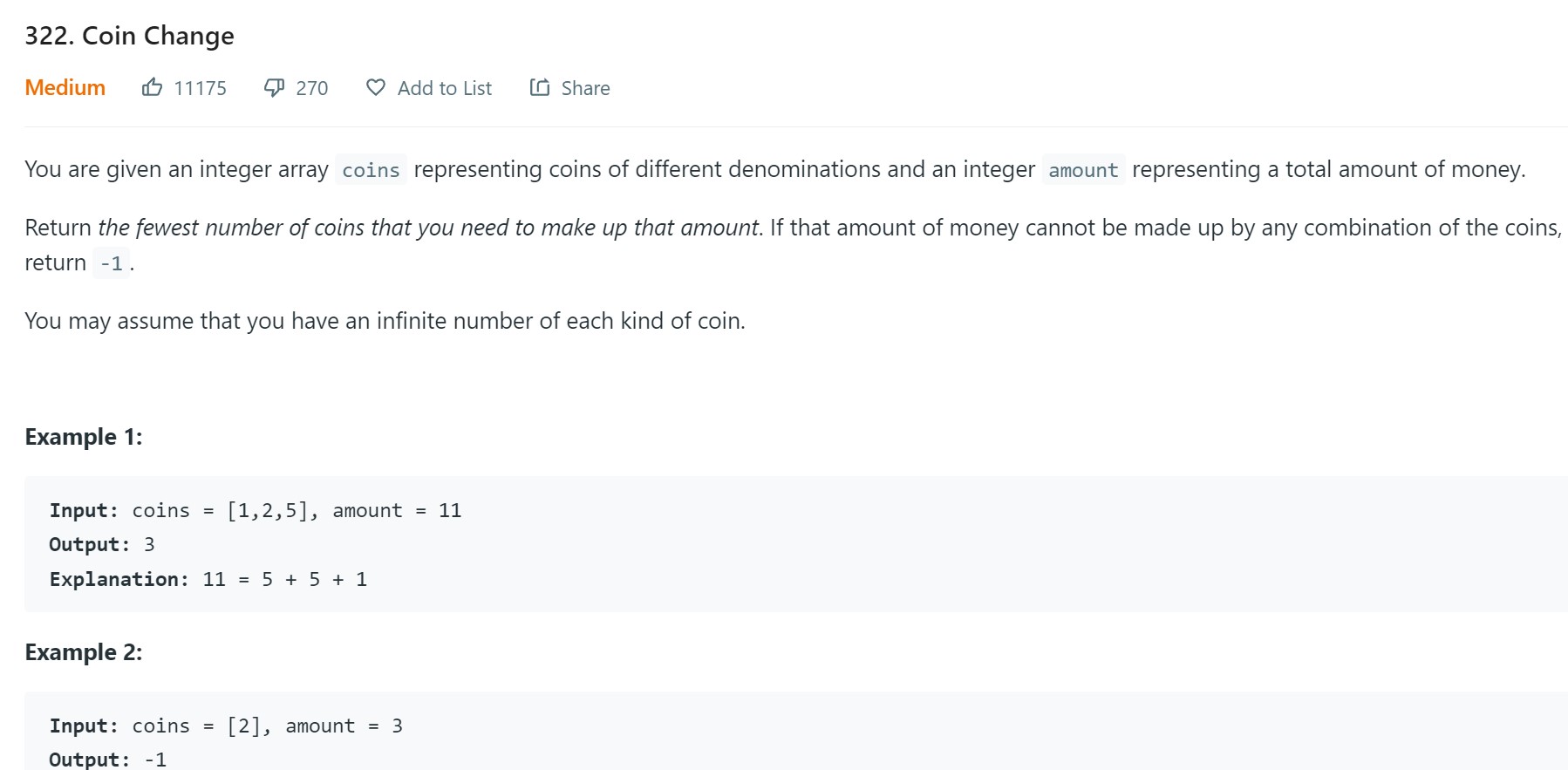
- 16. Coin Change - 322 - Medium
- References
Problems
1. Fibonacci Number - 509 - Easy
class Solution:
def fib(self, n: int) -> int:
firstnum = 0
secondnum = 1
if n == 0 or n == 1:
return n
for i in range(2, n+1):
sum = firstnum + secondnum
firstnum = secondnum
secondnum = sum
return sum
2. Number of ways of climing stairs - 70 -Easy
“Time Complexity”: “O(N)”, “Space Complexity”: “O(1)”
Points to Note:
- Number of ways of climbing one step = 1
- Number of ways of climbing two steps = 2
- Number of ways of climbing nth step from n-1 = 1
- So if there are f(n-1) ways to climb upto n-1 steps and f(n-2) ways to climb n-2 steps, then
- Number of ways of doing \(f(n-1) \text{OR} f(n-2) = f(n-1) + f(n-2)\)
Code
class Solution:
def climbStairs(self, n: int) -> int:
onestep = 1
twosteps = 2
if n == 1: return onestep
if n == 2: return twosteps
for i in range(3, n+1):
totalsteps = onestep + twosteps
onestep = twosteps
twosteps = totalsteps
return totalsteps
3: Minimum Cost of Climbing Stairs - 746 - Easy
Code
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
minimum_cost = [0] * (len(cost) + 1)
for i in range(2,len(cost)+1):
onestpcost = minimum_cost[i-1] + cost[i-1]
twostpcost = minimum_cost[i-2] + cost[i-2]
mincost = min(onestpcost, twostpcost)
minimum_cost[i] = mincost
return minimum_cost[-1]
Points to Note
-
Each step has a cost associated with it. We want to minimize the total cost. This is an optimization problem focusing on minimization.
-
Brute force could be to enumerate/compute the cost of each and all path and then find the minimum. The solution could be exponential numbers of path to enumerate and could take polynomial time.
-
We should make sure that we compute the cost for each path only once.
-
Applying decrease and conquer strategy, we focus on the last move. Either it could have come from the previous step or from previous to previous step.
-
Cost is given in the form of array or list.
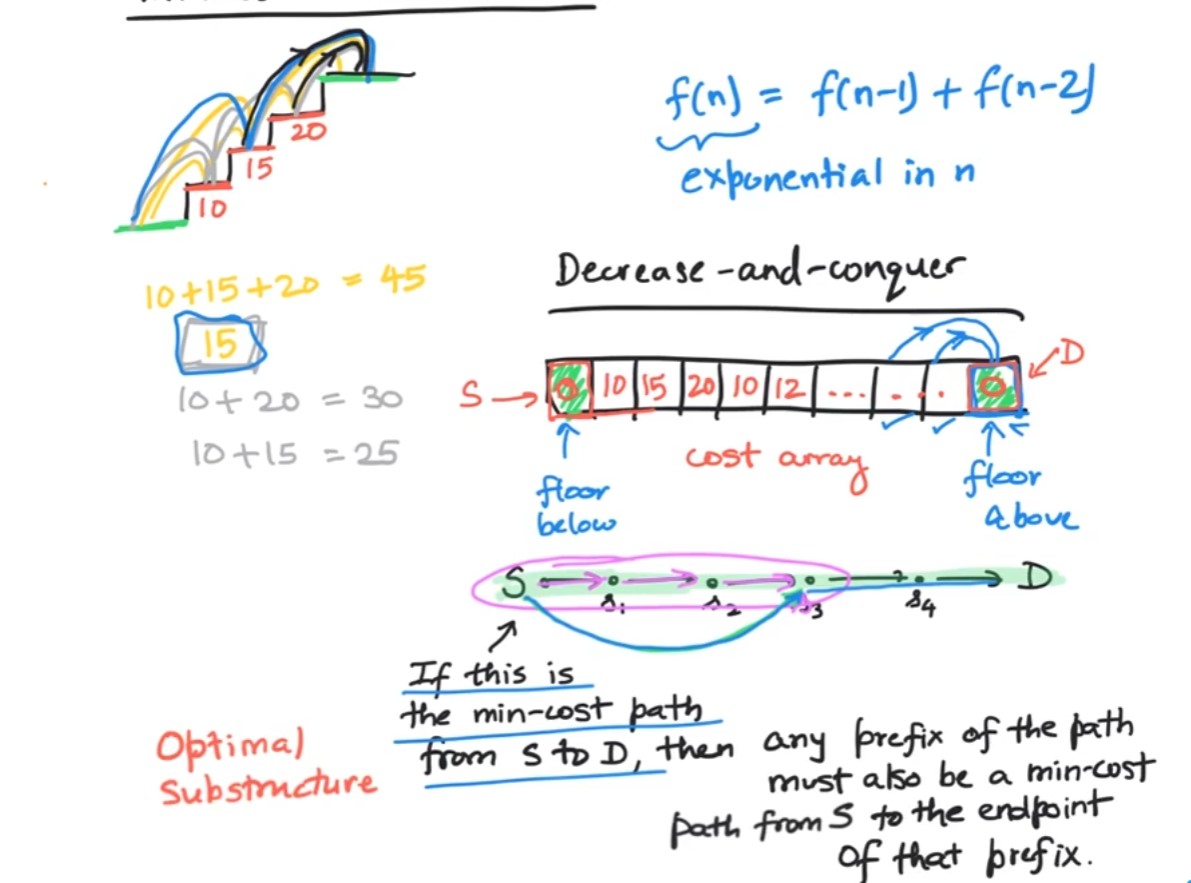
If there is a minimum cost path from source to destination, then any prefix of the path must also be a minimum-cost path from source to the end point of that prefix.
Because if there were a shorter path for the prefix, then I could have used this min path to the prefix and then walk to the D which is not possible. Thus, this problem has Optimal substructure.
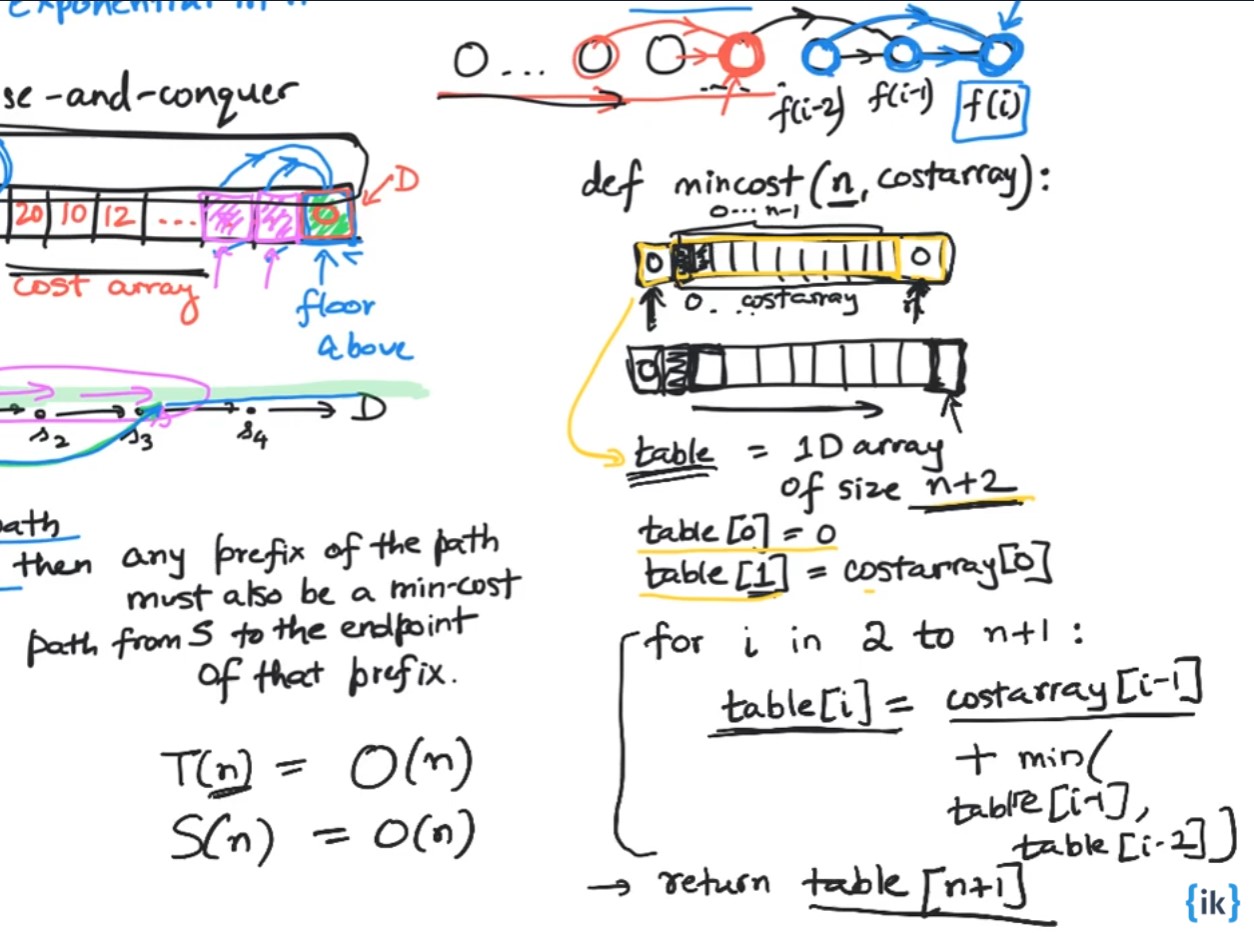
- Total number of sub problems is roughly n.
- We can use dependency graph to lay out the subproblem saying that value of a min cost path to a vertex can be the sum of the cost of the min cost path of the previous two vertices and pick whichever of them is minimum
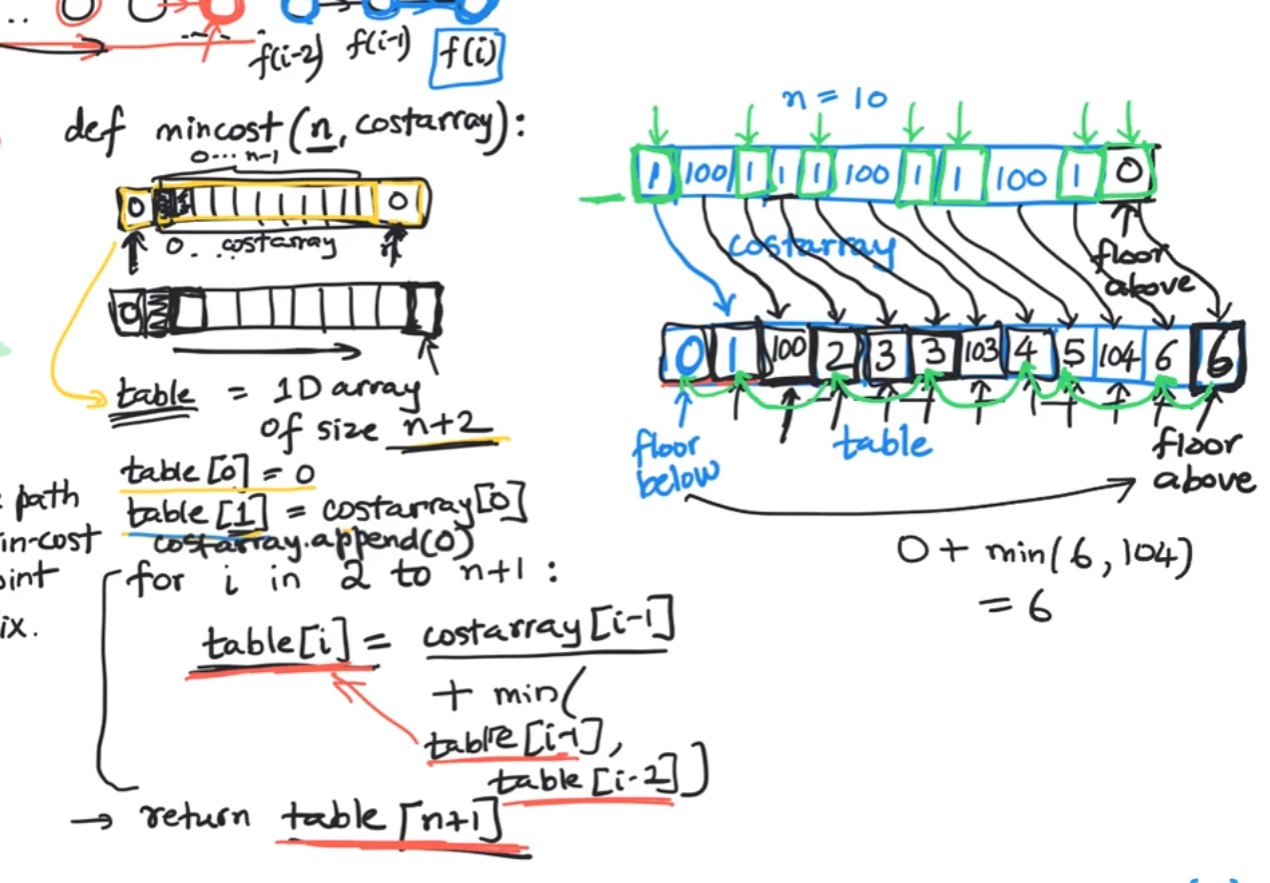
Complexity:
- Time Complexity: \(O(N)\)
- Space Complexity: \(O(N)\)
4. Unique Paths - LC 62 - Easy
Code
class Solution:
# DP approach
def uniquePaths(self, m: int, n: int) -> int:
table = [ [1 for j in range(m)] for i in range(n)]
for row in range(1, n):
for col in range(1, m):
table[row][col] = table[row-1][col] + table[row][col - 1]
return table[n-1][m-1]
# Recursion with memoization approach
def uniquePaths(self, m: int, n: int) -> int:
memo = [[0 for _ in range(n)] for _ in range(m)]
def paths(row, col):
if memo[row][col]:
return memo[row][col]
if row == 0 or col == 0:
memo[row][col] = 1
return memo[row][col]
memo[row][col] = paths(row-1, col) + paths(row, col-1)
return memo[row][col]
return paths(m-1, n-1)
Points to Note
- This problem is 2D version of number of ways of climbing stairs problem. This is a counting problem.
- We are given an m x n grid. From the 0,0 position, in how many ways can we reach the bottom right position of m,n given the constraints that we can only move down or right.
- This problem is a worded as path problem but it is same as \({n \choose k}\) problem.
- The grid values will be filled similar to pascal’s triangle and by filling the entire grid we can get the value of bottom right position.
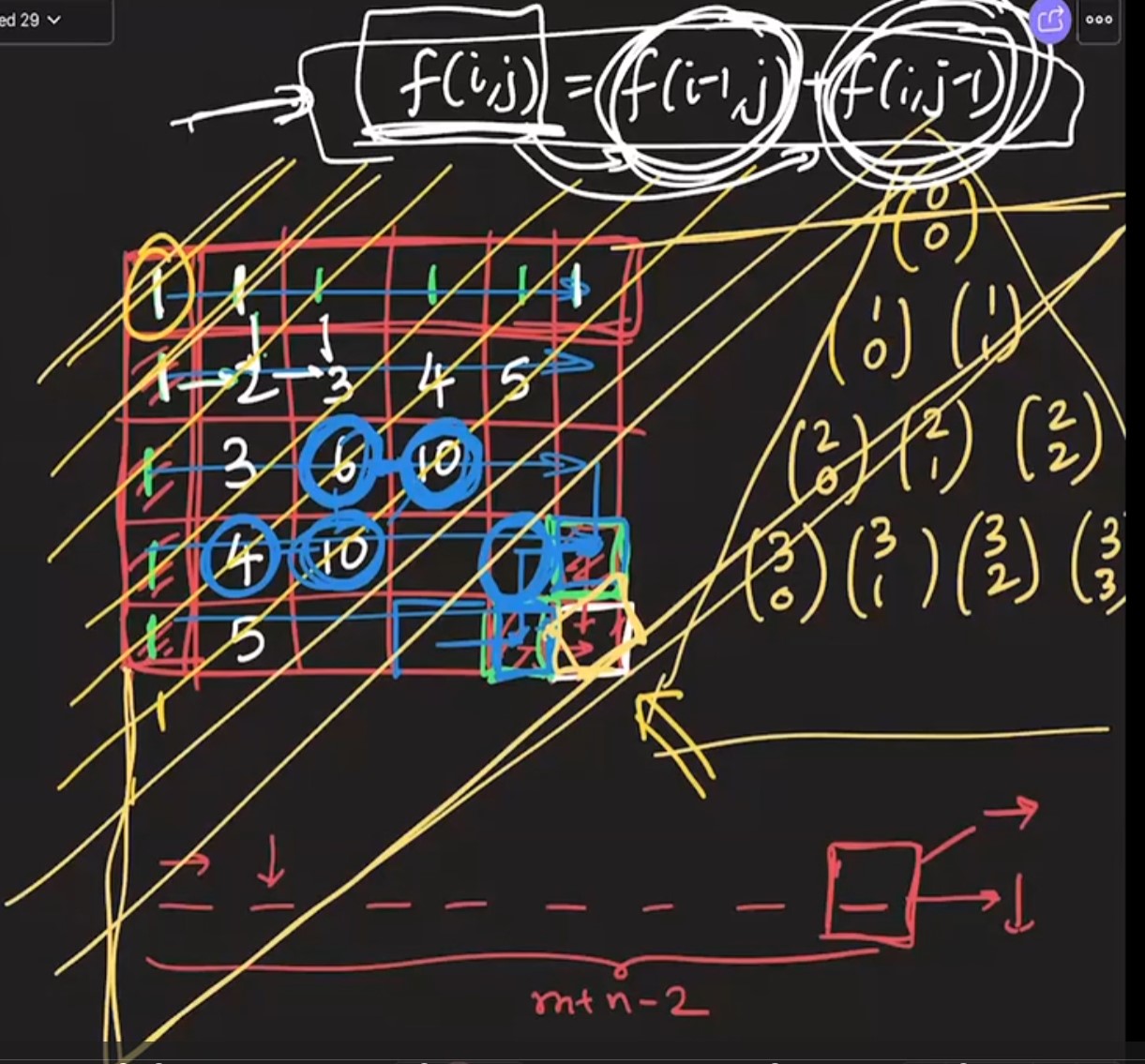
Mathematical Approach:
-
There are m-1 horizontal moves and n-1 vertical moves. So the total number of moves are: \(Total = (m-1) + (n-1) = m+n-2\)
-
Any path from top left to bottom right corner can be visualized as sequence of m+n-2 moves.
-
Permutation of horizontal and vertical moves.
-
We can pick which of these m+n-2 moves are horizontal and the rest will be vertical or vice versa.
-
So in how many ways can we pick these? \({m+n-2 \choose m-1}\) horizontal moves or \({m+n-2 \choose n-1}\) vertical moves.
Complexity Analysis
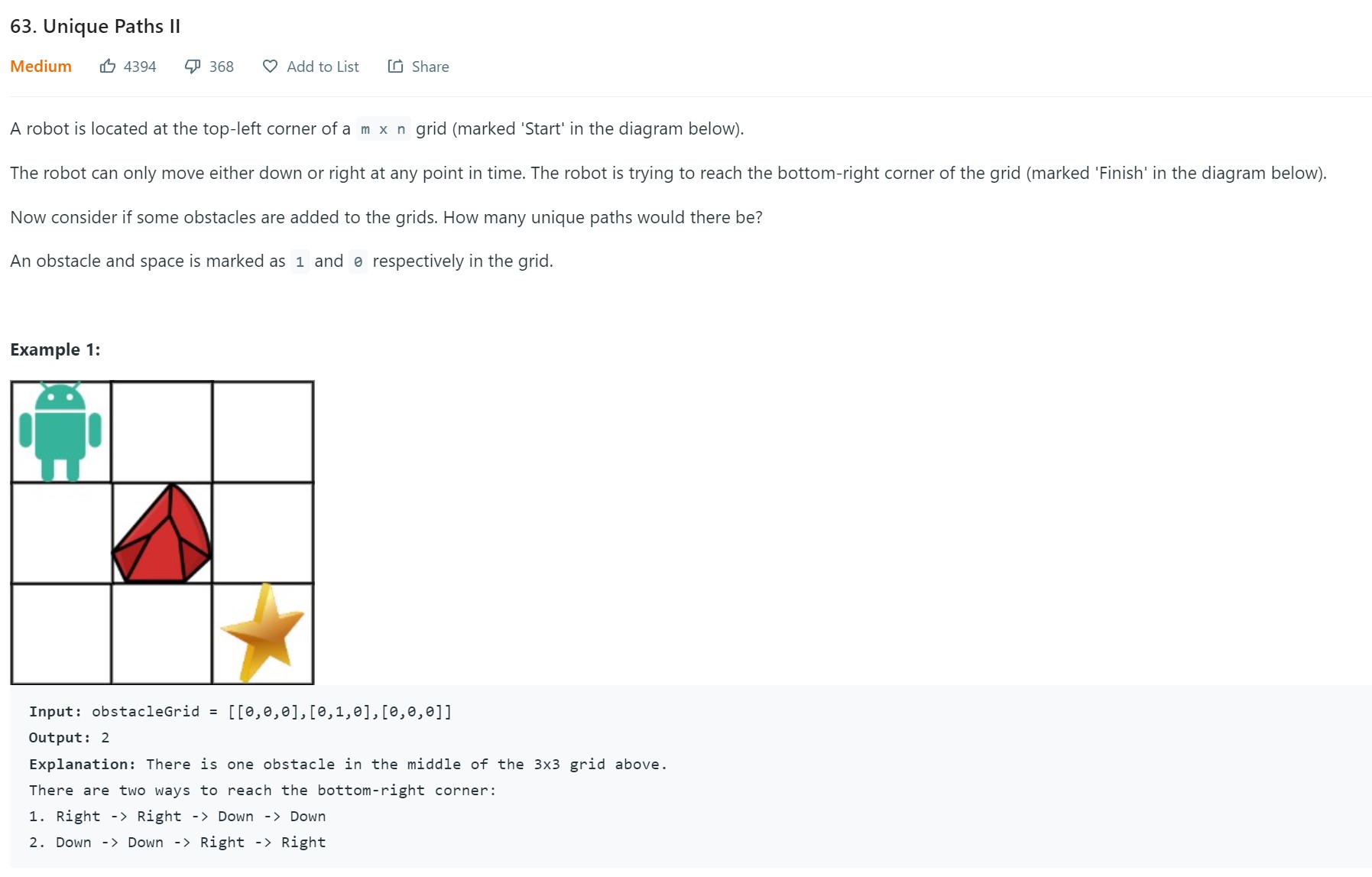
5. Unique Paths II - LC 63 - Medium
-1:38:35 has the space optimized code
Code
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
table = [[0 for j in range(len(obstacleGrid[0]))] for i in range(len(obstacleGrid))]
#Base Case
if obstacleGrid[0][0] == 1:
table[0][0] = 0
else:
table[0][0] = 1
# Fill Row 0
for col in range(1, len(obstacleGrid[0])):
if obstacleGrid[0][col] == 1:
table[0][col] = 0
else:
table[0][col] = table[0][col-1]
#Fill Col 0
for row in range(1, len(obstacleGrid)):
if obstacleGrid[row][0] == 1:
table[row][0] = 0
else:
table[row][0] = table[row-1][0]
# Main Traversal
for row in range(1, len(obstacleGrid)):
for col in range(1, len(obstacleGrid[0])):
if obstacleGrid[row][col] == 1:
table[row][col] = 0
else:
table[row][col] = table[row-1][col] + table[row][col-1]
return table[len(obstacleGrid) -1][len(obstacleGrid[0]) -1]
Points to Note
-
In Unique path problem, there was no obstacle…so the grid was not needed as input. Only the dimension of the grid was enough. In this problem, since there are obstacles in different parts of the grid, we need the grid info. as part of the problem.
-
Since the number of obstacles and locations of them are not known, we cannot use a clean mathematical formula as in unique path problem. We have to use decrease and conquer strategy as before.
-
Looking at the last cell or target cell, we have to think in how many ways the last but one cell can be reached to the left and also to its above cell. Extending it to the final cell is simply adding the total ways of these two.
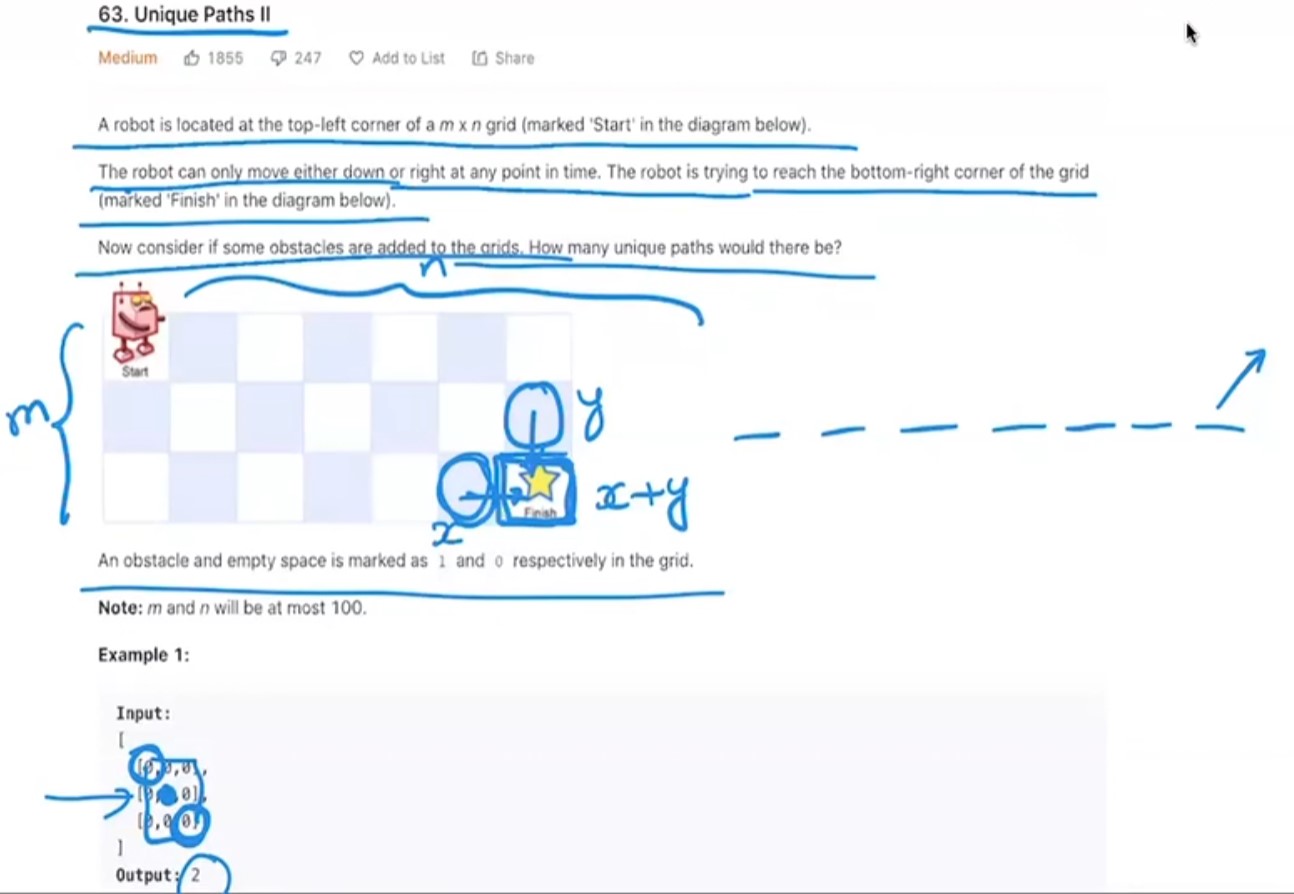
Complexity Analysis
- Time Complexity = \(O(mn)\)
- Space Compleixty = \(O(mn)\)
6. House Robber - LC 198 - Medium
Code
class Solution:
def rob(self, nums: List[int]) -> int:
if len(nums) == 0:
return 0
if len(nums) == 1:
return nums[0]
table = [0 for index in range(len(nums))]
#Base Cases
table[0] = nums[0]
table[1] = max(nums[0], nums[1])
#Recursive Case
# If last house is robbed, then prev house (n-2) cannot be robbed else it can be robbed (n-1)
for i in range(2, len(nums)):
table[i] = max(nums[i]+table[i-2], table[i-1])
return table[len(nums) - 1]
Points to Note
Complexity Analysis
7. House Robber II - LC 213 - Medium
Code
Points to Note
- The problem is in circular arrangement. Break it down to linear.
- If the first house is robbed, then its two neighbors on either side is not robbed.
- If the second house is robbed, then treat it as earlier house robber problem.
Complexity Analysis
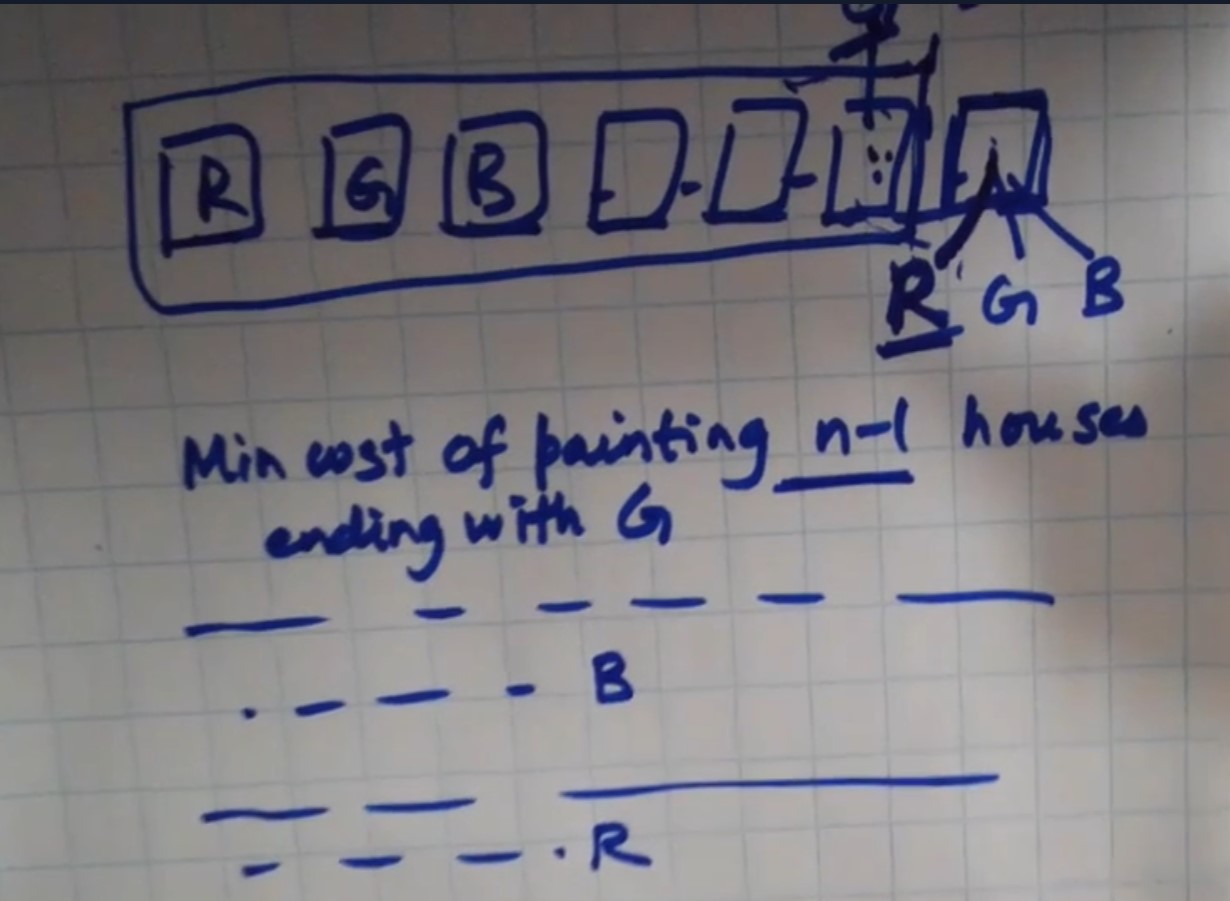
8. Paint house - 256 - Medium
Code
class Solution:
def minCost(self, costs: List[List[int]]) -> int:
if len(costs) == 0:
return 0
red = [0 for i in range(len(costs))]
blue = [0 for i in range(len(costs))]
green = [0 for i in range(len(costs))]
red[0] = costs[0][0]
blue[0] = costs[0][1]
green[0] = costs[0][2]
for i in range(1, len(costs)):
red[i] = costs[i][0] + min(blue[i-1], green[i-1])
blue[i] = costs[i][1] + min(red[i-1], green[i-1])
green[i] = costs[i][2] + min(red[i-1], blue[i-1])
return min(red[len(costs) - 1], blue[len(costs) - 1], green[len(costs) - 1])
Points to Note
Complexity Analysis
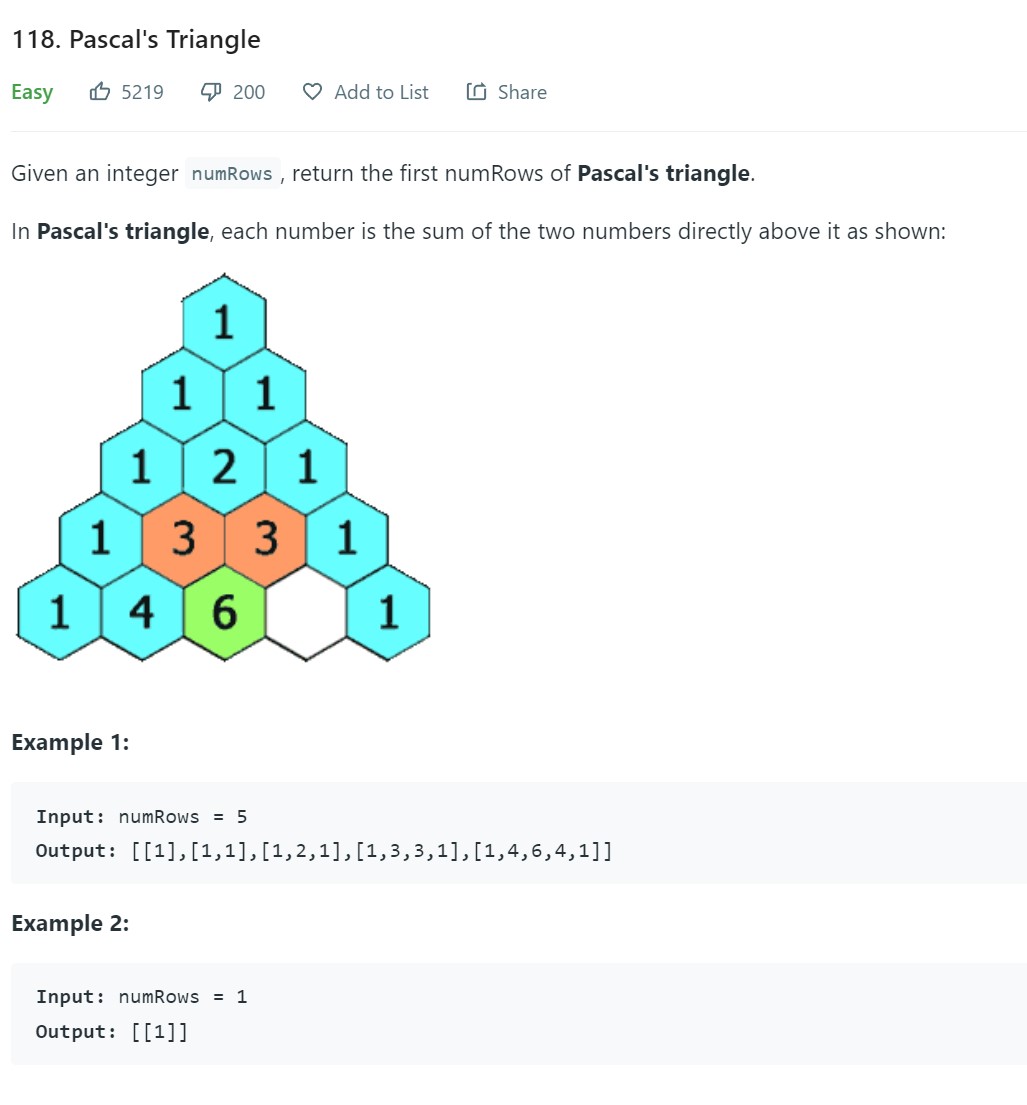
9. Pascal’s Triangle - 118 - Easy
Code
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
n = numRows - 1
table = [[1]*(row+1) for row in range(n+1)]
for row in range(2, len(table)):
for col in range(1, row):
table[row][col] = table[row-1][col] + table[row-1][col-1]
return table
Points to Note
- In some problems we get triangular arrays. This is one such problem
- We need to know how to create triangular table with variable number of columns in each row.
- In row \(n\), it will have all values of \({n \choose k}\) from \({n \choose 0}\) to \({ n\choose n}\). The number of columns will be \(n+1\)
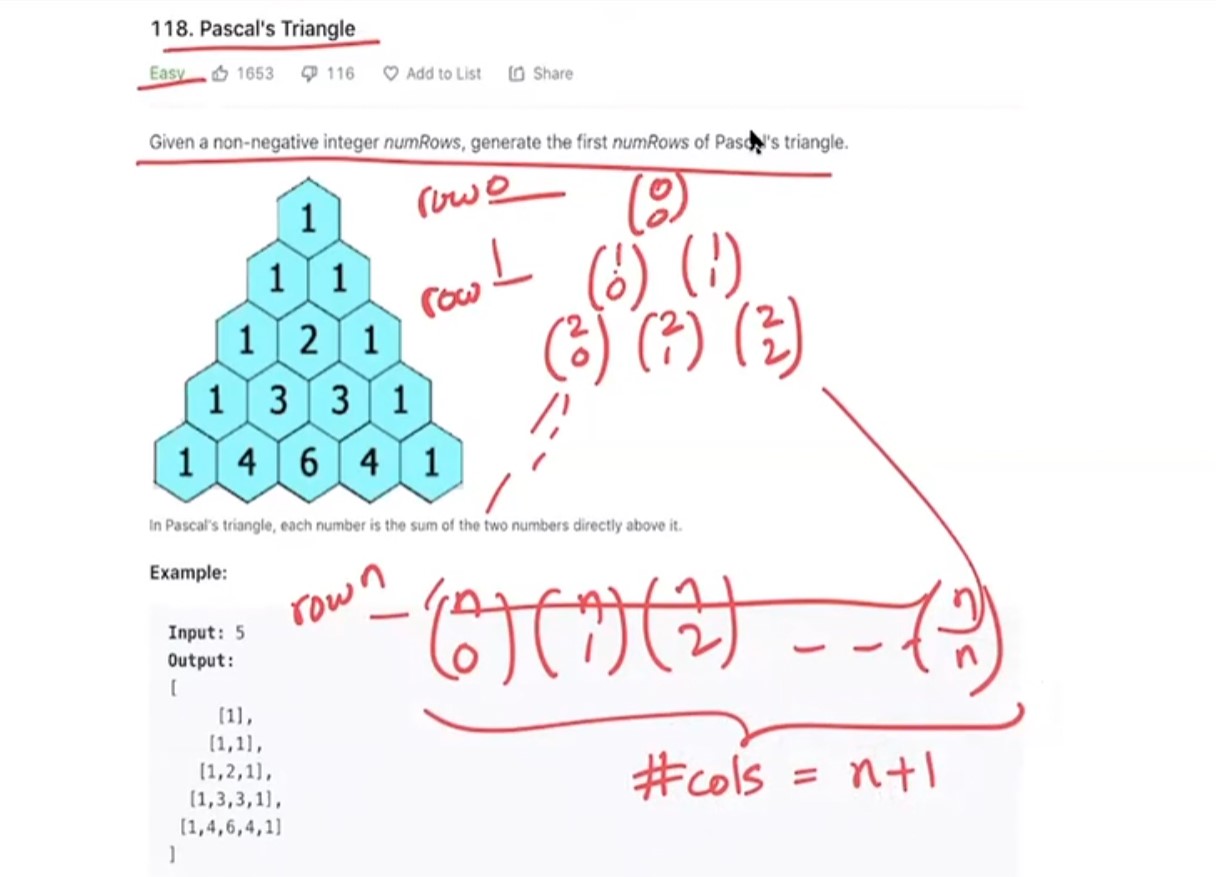
- To define a triangular array, initialize a 2D array with the number of rows equal to the given
numrowsinput in the problem. - For each row, the number of columns differ and the pattern is:
\[\begin{eqnarray} \text{row 0} = \text{1 column} \\\ \text{row 1} = \text{2 columns} \\\ \text{row i} = \text{i+1 columns} \end{eqnarray}\]
- In triangular arrays, boundary is very tricky. Pay special attention in initialization stage to know number of rows and tables.
- If the entire table is initialized to 1, then we do not require base case to set first and last columns to 1.
Complexity Analysis
- Time Complexity: \(O(n^2)\)
- Space Complexity: \(O(n^2)\)
10. Triangle - 120 - Medium
-
2:06:04 - Triangle
-
Alternative Class - Dynamic PRogramming with Omkar - 2:06:04
References:
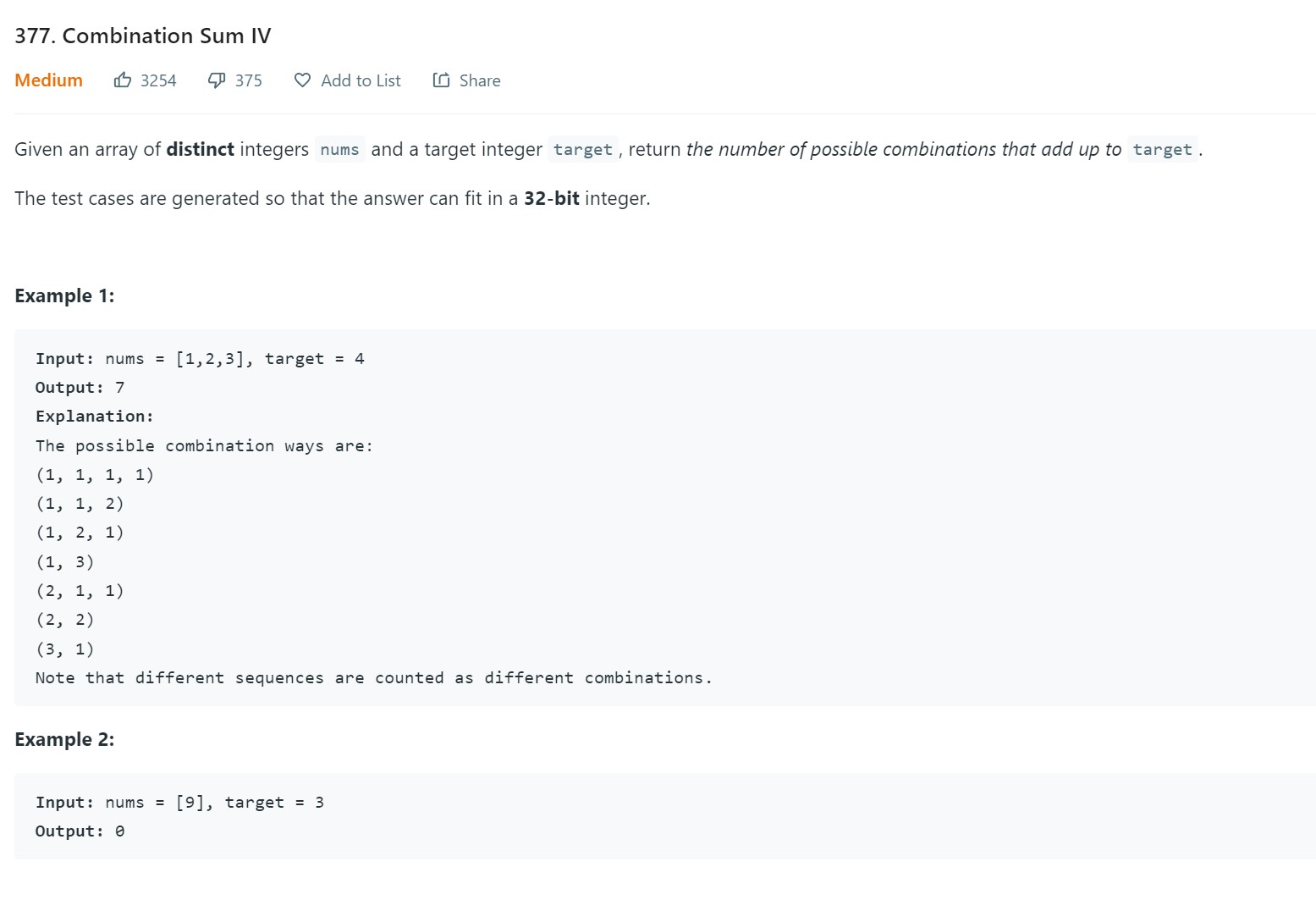
11. Combination Sum IV - 377 - Medium
Code
class Solution:
def combinationSum4(self, nums: List[int], target: int) -> int:
table = [0] * (1+target)
table[0] = 1
for i in range(1, 1+target):
for num in nums:
if i - num >= 0:
table[i] += table[i-num]
return table[-1]
Points to Note
-
This is coin change count (permutation version) and there is subset version as well as optimization problem. Though problem title says ‘Combination’, it is permutation problem. The word combination is used at higher level such as to represent ‘combinotorial problem’ where order matters.
-
The american coin problem can be approached with greedy algorithm (since the denomination is in multiples). Otherwise greedy approach does not work for this problem.
-
The goal is to count the number of ways in which the coin denominations add up to the target amount.
-
In this problem, we can pick the same choice as many times as possible. In other words, order matters. Not just counting the copies of the denominations make up the target, we need to treat different arrangements of the same set of coins as distinct choice.
-
Brute force approach is to exhaustively check all the combinations/subsets and see how many add up to the target. This takes exponential time.
-
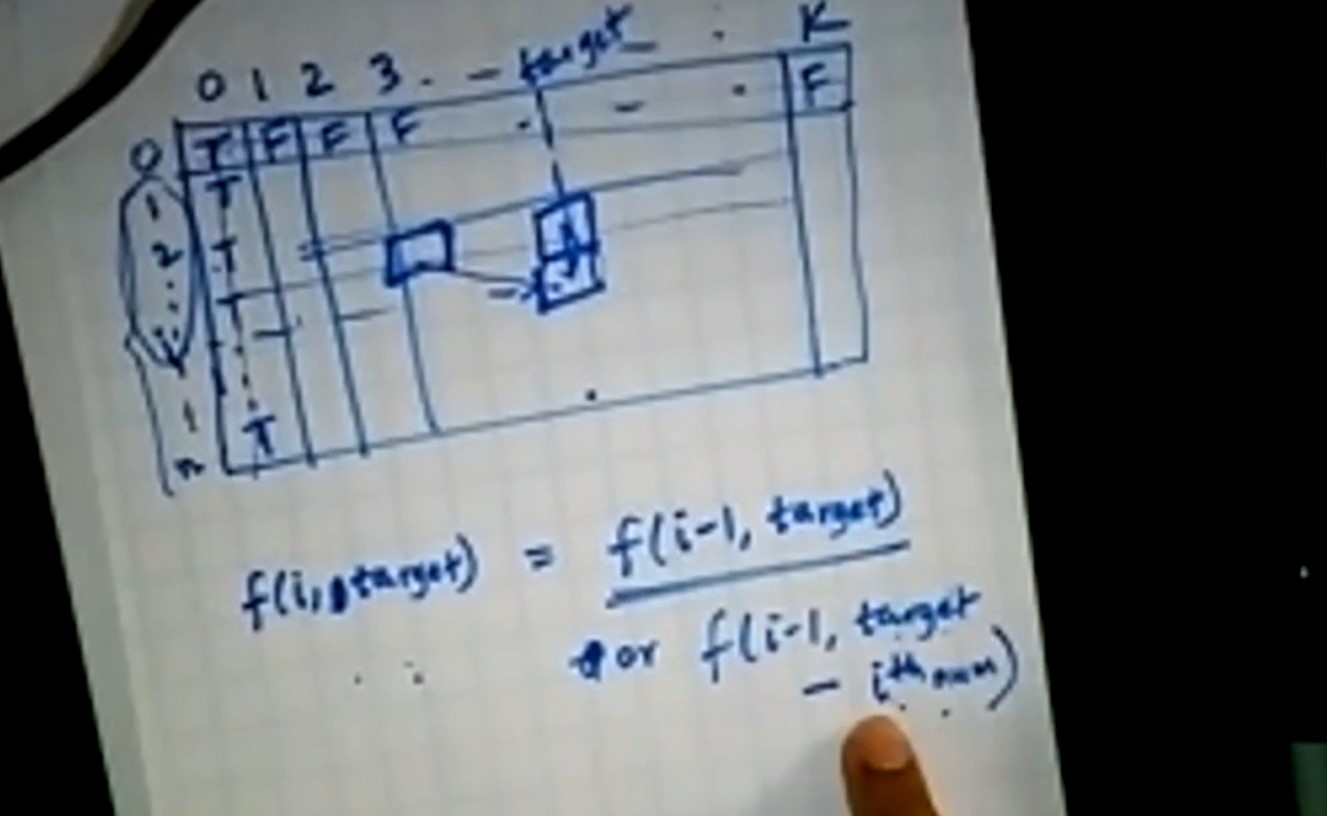
How many distinct sub problems we get by eliminating the redundancy?
- Each subproblem depends on two other subproblem.
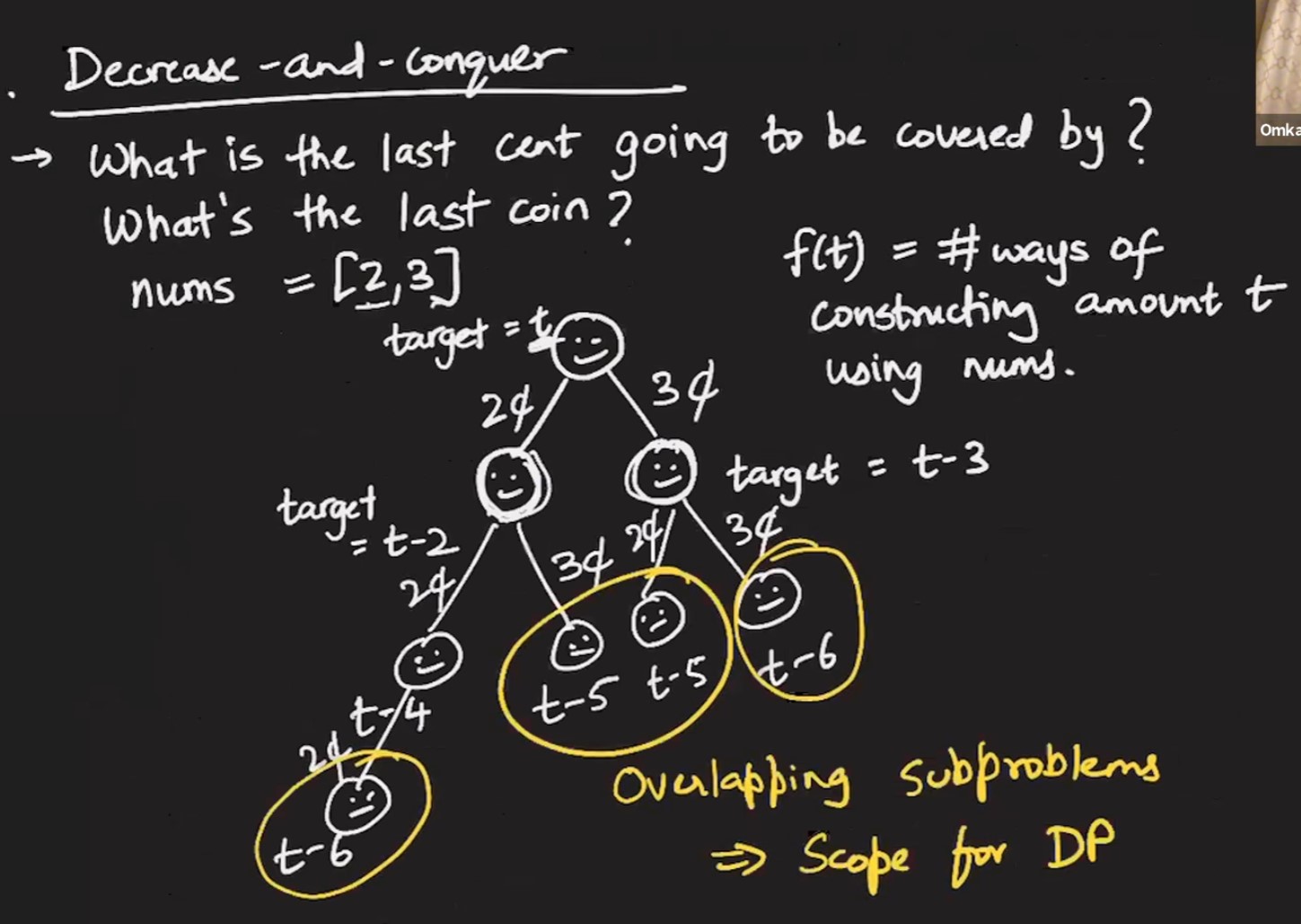
- How to initialize the table for the base case ? There is only one way to get a sum of 0 …empty set.
- If the target is 25, then we have to look 24 steps behind 0 but since it does not make sense, we will any value less than 0 as 0.

Complexity Analysis
- Time Complexity: \(O(n \times t)\)
- Space Complexity: \(O(t)\)
Edit Distance:
- Cost is same. minimize number of operations withotu differentinatg between the three
- each pair can be represented as a pair waise aalignment
- Number of alignemnts I can create is exponential \(n \choose k\)
- maximum number of alignment is length of two strings.



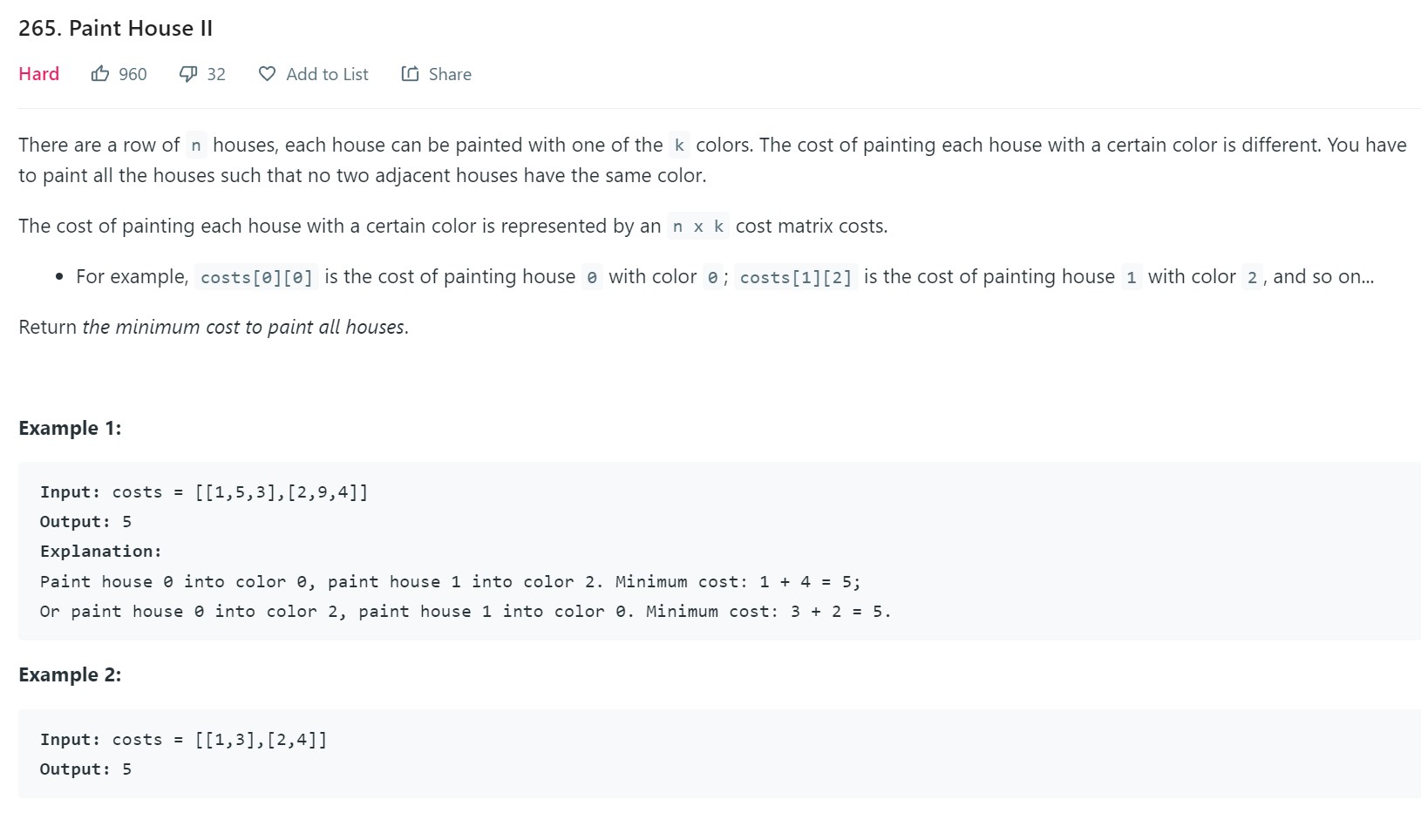
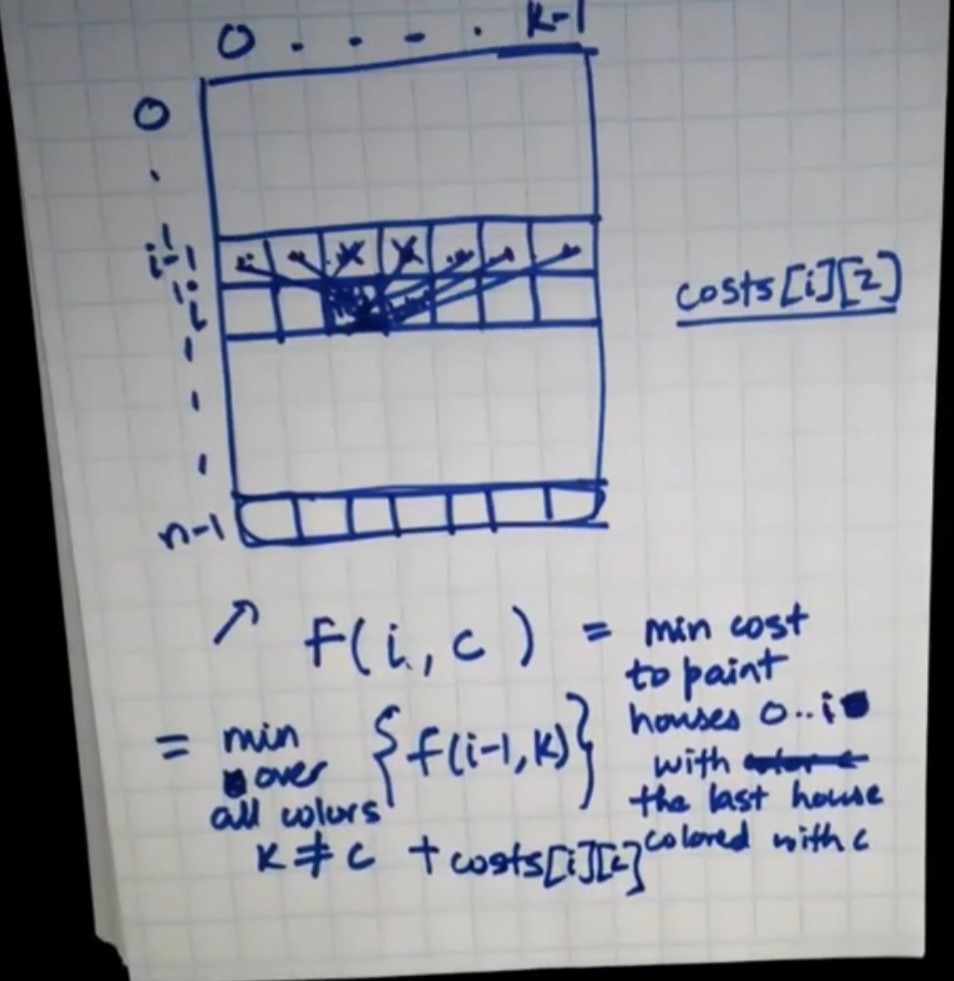
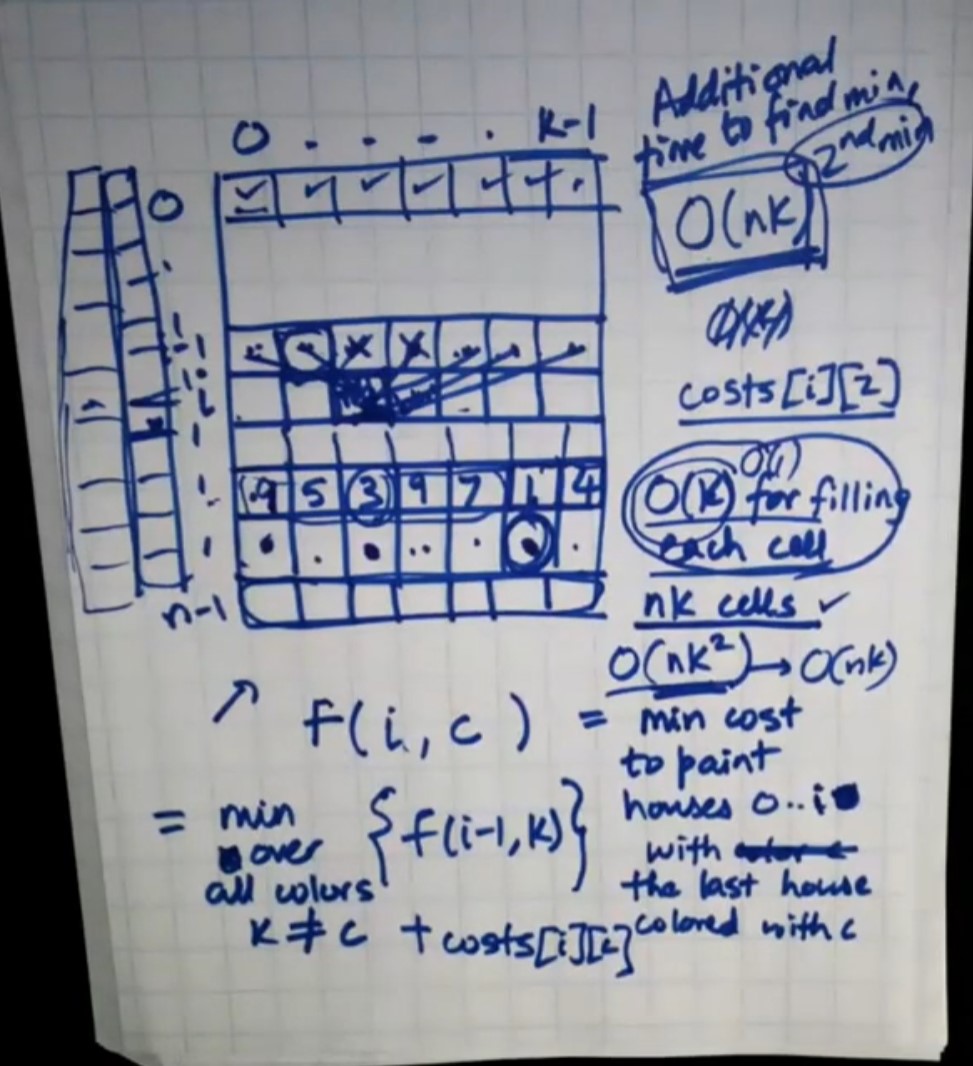
12. Paint House II - 265 - Hard
Code
class Solution:
def minCostII(self, costs: List[List[int]]) -> int:
n = len(costs)
if n == 0:
return 0
k = len(costs[0])
table = [ [0 for _ in range(k)] for _ in range(n)]
#Base Case
for color in range(k):
table[0][color] = costs[0][color]
#Main Traversal
for i in range(1, n):
#For each house i, compute the best way to color the houses up to that house ending with each specific color
for color in range(k):
best = float("inf")
for prevcolor in range(k):
if prevcolor == color:
continue
best = min(best, table[i-1][prevcolor])
table[i][color] = best + costs[i][color]
return min(table[-1])
Points to Note
- Just knowing the optimal cost of n-1 is not enough. We need additional color information too.
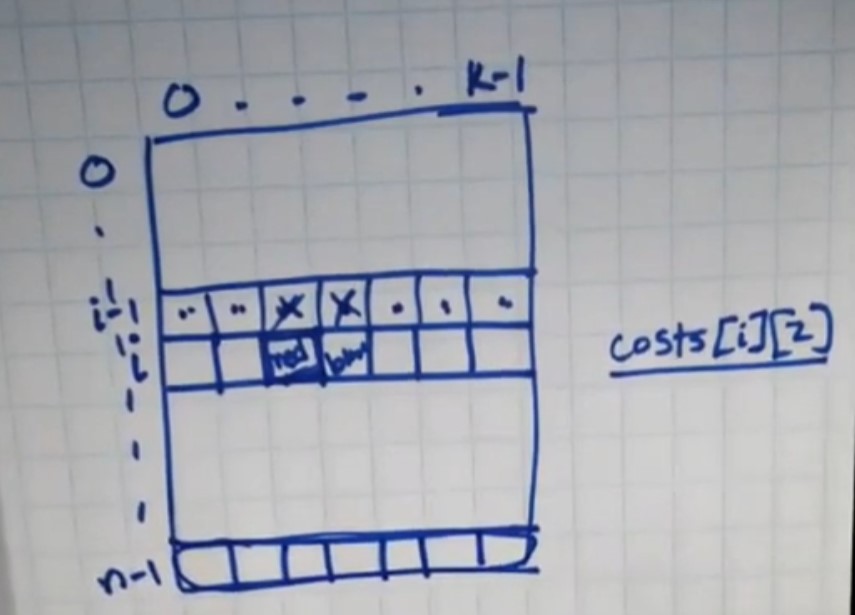
- To understand this problem, review paint house problem to begin with.


Complexity Analysis
- Time Complexity: \(O(n \times k^2)\)
- Space Complexity: \(O(nk)\)
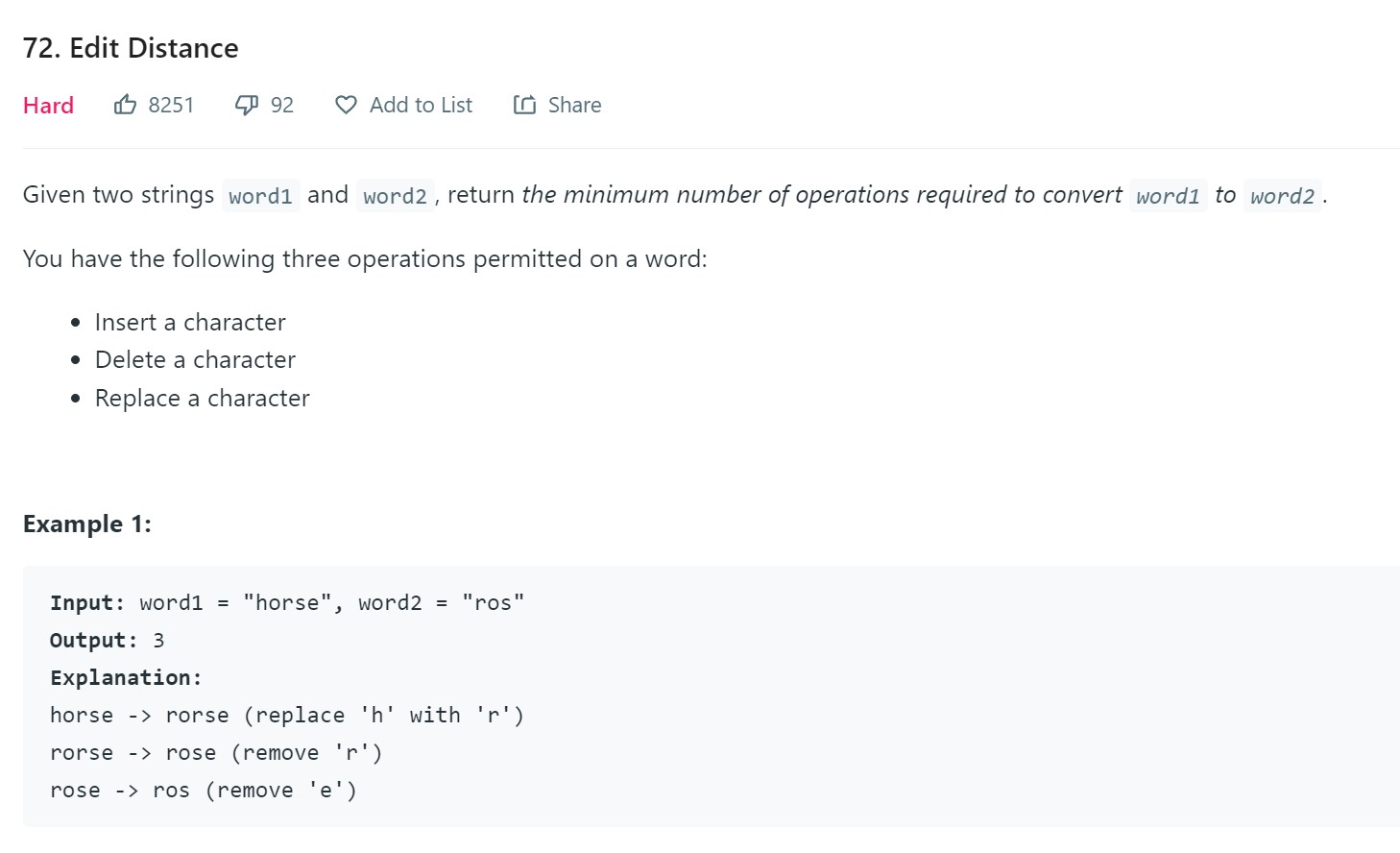
13. Edit Distance - 72 - Hard
Code
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
table = [[0 for _ in range(1+len(word2))] for _ in range(1+len(word1))]
for col in range(1,1+len(word2)):
table[0][col] = col
for row in range(1, 1+len(word1)):
table[row][0] = row
for row in range(1, 1+len(word1)):
for col in range(1, 1+len(word2)):
if word1[row-1] == word2[col-1]:
s = 0
else:
s = 1
table[row][col] = min(table[row-1][col] + 1, table[row][col-1] + 1, table[row-1][col-1] +s)
return table[-1][-1]
Points to Note
Edit Distance:
- Cost is same. minimize number of operations withotu differentinatg between the three
- each pair can be represented as a pair waise aalignment
- Number of alignemnts I can create is exponential \(n \choose k\)
- maximum number of alignment is length of two strings.


Complexity Analysis
14. Longest Common Subsequence - 1143 - Medium
Code
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
table = [ [0 for _ in range(1+len(text2))] for _ in range(1+len(text1))]
for row in range(1, 1+len(text1)):
for col in range(1, 1+len(text2)):
if text1[row-1] == text2[col-1]:
s=1
else:
s = 0
table[row][col] = max(table[row-1][col], table[row][col-1], table[row-1][col-1] + s)
return table[-1][-1]
Points to Note
-
Substring and Subsequence problems are two separate categories. Since they sound similar, we should not assume that the problems are of similar nature.
-
Substring: Given a string, how many possible substrings are there in a string? There are \(O(n^2)\). For two strings, the complexity would be \(O(n^2)\) for first string and \(O(n^2)\) for the second string totalling up to \(O(n^4)\). This is clearly not a combinatorial optimization problem.
-
Substring belongs to string class.
-
Subsequence: How many subsequence can we form given a string of length N? = \(O(2^N)\) because for each character we have the choice of include or exclude in the subsequence. For two strings, this is clearly exponential \(O(2^N)\) for first string and \(O(2^N)\) for the second string resulting in a exponential problem whereas substring problem is of polynomial nature.
-
Longest subsequence is similar to Edit distance but we are trying to maximizing instead of minimizing.
Difference between Edit Distance and LCS:
-
There is only slight difference between these two problems.
-
Visualize the common subsequence in terms of alignment similar to Edit Distance.
-
The LCS consists of characters that are common to both sequences. We want those characters to align up.
-
Instead of two sequences, we want a final sequence where we want to pair up characters and maximize the length of common subsequence.
-
If the given two strings are M and N, in any alignment, we add the both characters, then the sum will be M + N characters.
-
Every time there is insertion, there is single character appear in the pair, for deletion, there is single character appear in the pair and for every time there is substitution, for match or mismatch, we have 2 characters appear in the pair.
-
Is this reverse of Edit Distance problem? in other words, minimizing insertion, deletion and substitution (Edit Distance problem) is equivalent to maximizing the number of matches? Looks like it is not the case given that we have 2 times substitution.. The ‘2’ here makes it behave differently.
-
If the equations were:
\[\begin{eqnarray} \text{No. of insertions + No. of deletions + No of mis matches + No. of matches} \nonumber \\\ \text{then minimizing No. of insertions + No. of deletions + No of mis matches} \nonumber \\\ \boxed{\text{is same as maximizing No of matches}} \end{eqnarray}\]
However, this is not the case given we have two substitutions.
Approach to solve:
-
Instead of minimizing cost, we are maximizing reward. Everytime we find common char, we increase the reward by 1. Reward for mismatch, insertion and deletion = 0.
-
Assume we can combine the two strings into alignment that maximizes the matches.
-
Focusing on the last step, I have three choices… Insertion, deletion or substitution. If optimial solution corresponds to this alignment, then prefix is also maximized for the same alignment. There is optimal substructure.
-
The argument is that:
\[ \boxed{\text{prefix of an optimal solution must be optimal}} \]
We can argue this using proof by contradiction. If the solution was not optimal for the prefix, we could have used/replaced it by better solution.
\[\begin{align} f(i,j) = \text{length of LCS of} x_1, x_2, x_3…x_i \text{ and } y_1, y_2, y_3…y_j \nonumber \\\ \text{where } i = [0, m] \text{ and } j = [0,n] \end{align}\] maximize LCS = \[\begin{cases} f(i-1, j) = 0 \\\ f(i, j-1) = 0\\\ f(i-1, j-1) + s = & \text{1 if $x_i$ = $y_j$ else 0} \end{cases}\]
Base Case: \[\begin{align} f(i,0) = 0 \enspace \enspace \forall i \newline f(0, j) = 0 \enspace \enspace \forall j \end{align}\]
- Since the base case is 0, we can create the table with 0 and avoid an initialization loop.
- We can go in the topological sort order and calculate the reward and maximize it. When we make the diagonal move, we are aligning the two sequences. Not all diagonal moves provide the optimal solution. There could be lots of partial solutions. (these could be for matches or mismatches) and we need to count only matches.
Complexity Analysis
15. Delete Operations for two strings - 583 - Medium
Code
Points to Note
How to choose DB in system design interviews Is ticket price tied to the seat/category or the price depends on the show?
Complexity Analysis
16. Coin Change - 322 - Medium
Code
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
table = [ [0 for _ in range(1+len(text2))] for _ in range(1+len(text1))]
for row in range(1, 1+len(text1)):
for col in range(1, 1+len(text2)):
if text1[row-1] == text2[col-1]:
s=1
else:
s = 0
table[row][col] = max(table[row-1][col], table[row][col-1], table[row-1][col-1] + s)
return table[-1][-1]
Points to Note
-
Since the question is about finding the fewest number of coins, this is clearly an optimization/minimization problem.
-
Is there optimal substructure?
-
If the equations were:
\[\begin{eqnarray} \text{No. of insertions + No. of deletions + No of mis matches + No. of matches} \nonumber \\\ \text{then minimizing No. of insertions + No. of deletions + No of mis matches} \nonumber \\\ \boxed{\text{is same as maximizing No of matches}} \end{eqnarray}\]
\[\begin{align} f(i,j) = \text{length of LCS of} x_1, x_2, x_3…x_i \text{ and } y_1, y_2, y_3…y_j \nonumber \\\ \text{where } i = [0, m] \text{ and } j = [0,n] \end{align}\] maximize LCS = \[\begin{cases} f(i-1, j) = 0 \\\ f(i, j-1) = 0\\\ f(i-1, j-1) + s = & \text{1 if $x_i$ = $y_j$ else 0} \end{cases}\]
Base Case: \[\begin{align} f(i,0) = 0 \enspace \enspace \forall i \newline f(0, j) = 0 \enspace \enspace \forall j \end{align}\]