Graph Problems

Table of Contents

Problems
Solutions by type
References:

Problems

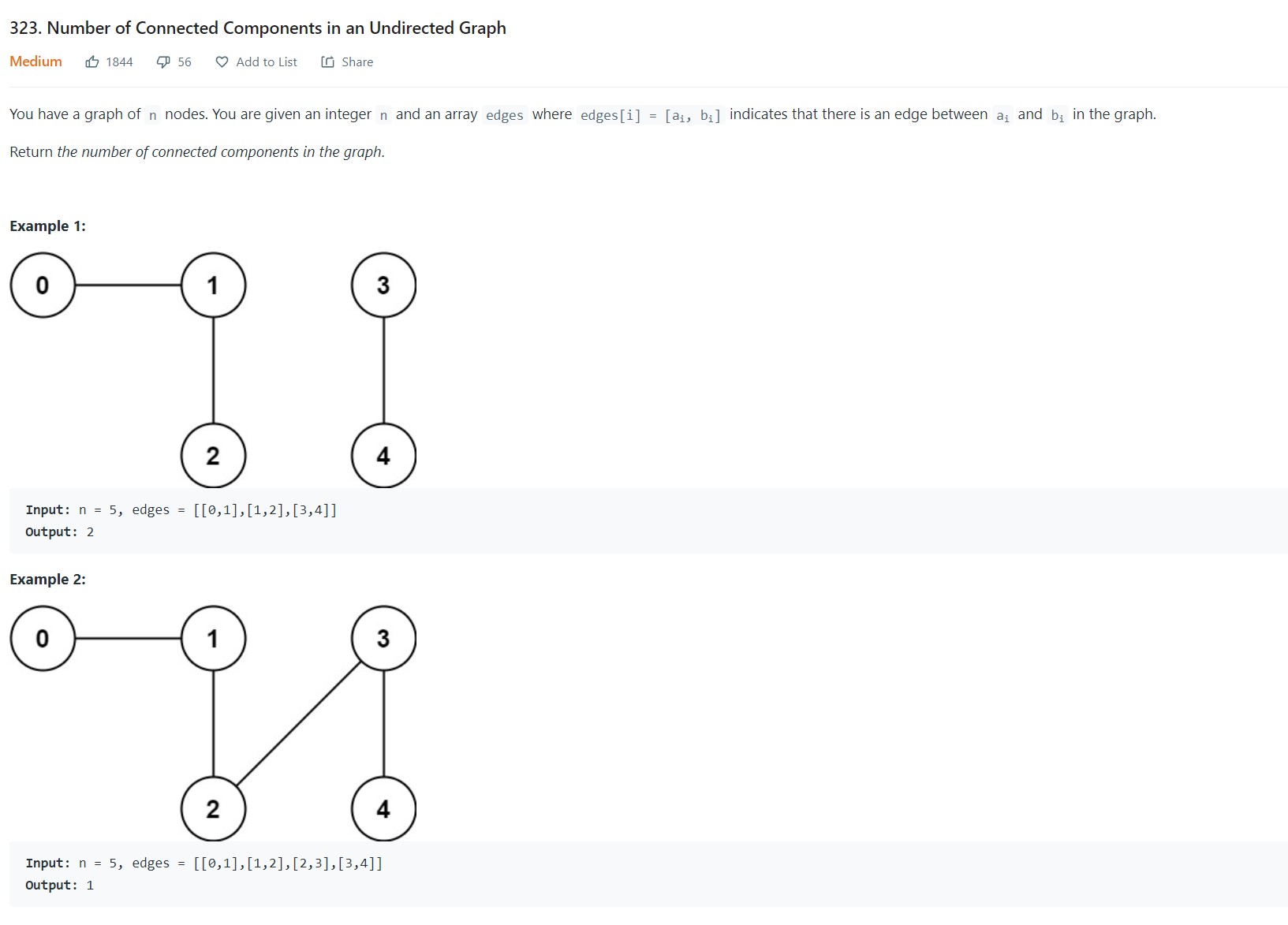
1. Number of connected components in an undirected graph - LC 323 - Medium

Code


   ## DFS Version with Recursion
     class Solution:
       def countComponents(self, n: int, edges: List[List[int]]) -> int:
	   adjlist = [[] for _ in range(n)]
	   # Build Graph
	   for (src, dst) in edges:
	       adjlist[src].append(dst)
	       adjlist[dst].append(src)
	   visited = [-1] * n
	   # Write dfs or bfs search
	   def dfs(source):
	       visited[source] = 1
	       for neighbor in adjlist[source]:
		   if visited[neighbor] == -1:
		       dfs(neighbor)
	   # Outer loop to traverse all the vertices
	   components = 0
	   for v in range(n):
	       if visited[v] == -1:
		   components += 1
		   dfs(v)
	   return components

  ## BFS version with queue

class Solution:
    def countComponents(self, n: int, edges: List[List[int]]) -> int:

	adjlist = [[] for _ in range(n)]
	visited = [-1] * n
	components = 0

	# Step 1: Build Graph
	for (src, dst) in edges:
	    adjlist[src].append(dst)
	    adjlist[dst].append(src)

	# Step 2: Write dfs or bfs search
	def bfs(source):
	    visited[source] = 1
	    q = collections.deque([source])
	    while len(q):
		node = q.popleft()
		for neighbor in adjlist[node]:
		    if visited[neighbor] == -1:
			visited[neighbor] = 1
			q.append(neighbor)

	# Step 3: Outer loop to traverse all the vertices
	for v in range(n):
	    if visited[v] == -1:
		components += 1
		bfs(v)

	return components

Points to Note

Depending on the queue space vs stack space, we can choose BFS or DFS for this problem as time and space complexity are the same.

Complexity Analysis

BFS and DFS roughly run in the same time complexity

Time Complexity: BFS:

One by one each vertex is pushed into the queue and popped from the queue. This HAS TO HAPPEN for every vertex whether in single or multiple bfs()
Time taken to push and pop a node to queue is constant. So across all nodes, if this is done, it takes O(N) time.
In the inside for loop, every time a node is popped out, we look at all the neighbors. The cost of looking up the adjacency list for each node for all neighbors is O(degree of node). This has to be done for every node in the graph.
- Sum of all degrees of vertex in undirected graph = twice the edges (since it is undirected) = O(m)
Total cost = O(m + n) Since we do not know which one is bigger, we

leave here. Otherwise it is the max of m or n.

Space Compelexity:

Adjlist has its own sace complexity. Every vertex in the array = O(n) and the list of neighbors = O(m) = O(m+n)
The size of the queue = O(N) assuming worst case where source vertex is connected to all other vertices in the graph
Total cost = O(m + n)

DFS: Time Complexity:

Push and pop of vertices from stack (instead of queue) is constant. For n vertices it is O(n)
The inner loop is looking up all the neighbors of a node in the adjacent list = O(m)
Total cost is same as bfs = O(m + n)

Space Complexity:

The call stack space can get at the maximum of O(n). This is the height of the tree at the max.

Coding Mistakes

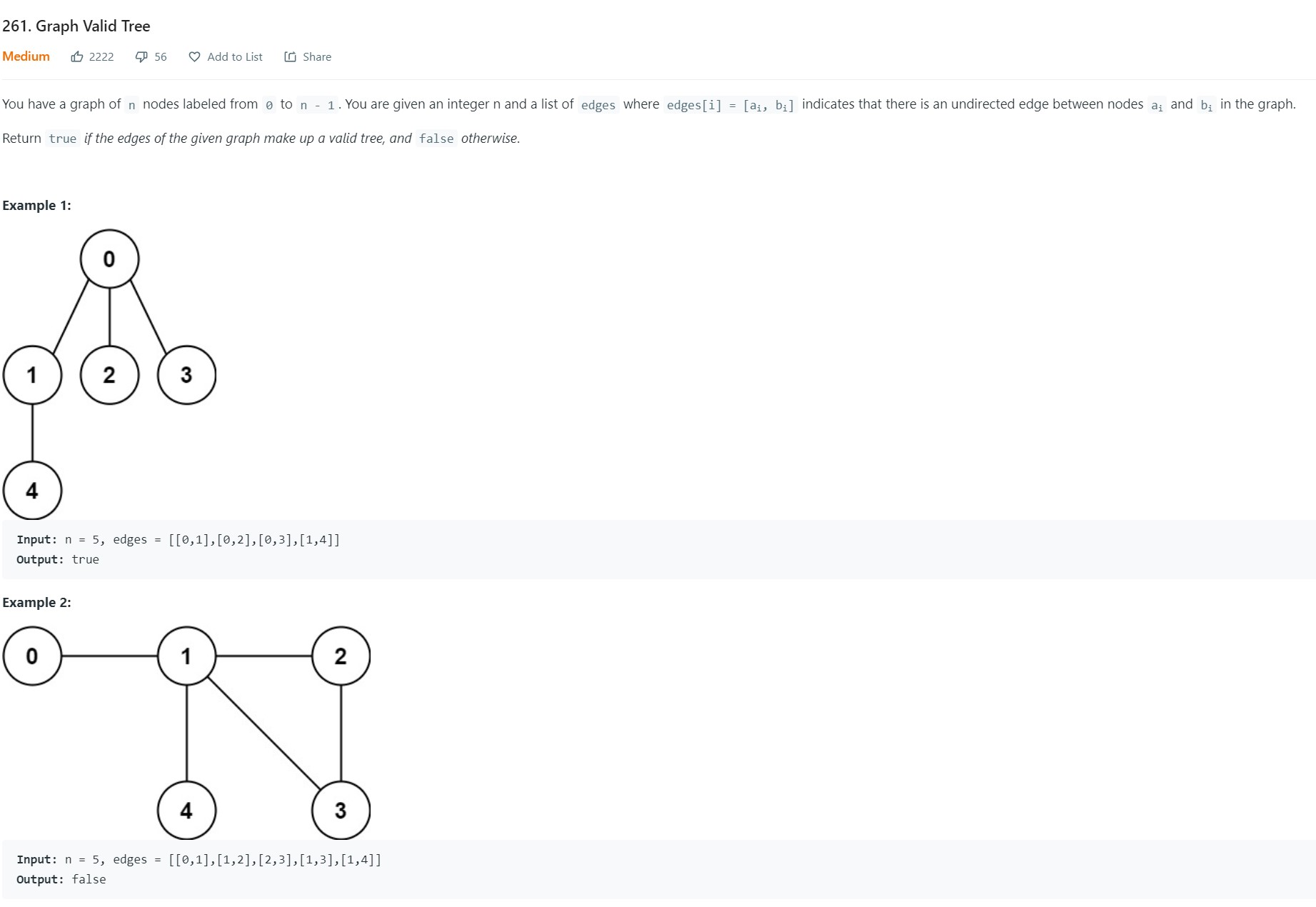
2. Graph Valid Tree - LC 261 - Medium

Code

class Solution:
    def validTree(self, n: int, edges: List[List[int]]) -> bool:
	# Variables
	component = 0
	visited = [-1] * n
	adjlist = [[] for _ in range(n)]
	parent = [-1] * n
	#build graph

	for (src, dst) in edges:
	    adjlist[src].append(dst)
	    adjlist[dst].append(src)

	# build bfs or dfs

	def bfs(node):
	    q = deque([node])
	    visited[node] = 1
	    while len(q):
		node = q.popleft()
		for neighbor in adjlist[node]:
		    if visited[neighbor] == -1:
			visited[neighbor] = 1
			parent[neighbor] = node
			q.append(neighbor)
		    else:
			if neighbor != parent[node]:
			    #This means the neighbor's parent and node's parent are not the same. Hence there is cycle
			    return True
	    return False

	# Loop through all the vertices

	for v in range(n):
	    if visited[v] == -1:
		component += 1
		iscycle = bfs(v)
	    #Back track if there is more than one component because it cannot be a tree then
	    if component > 1 or iscycle:
		return False
	return True

Points to Note

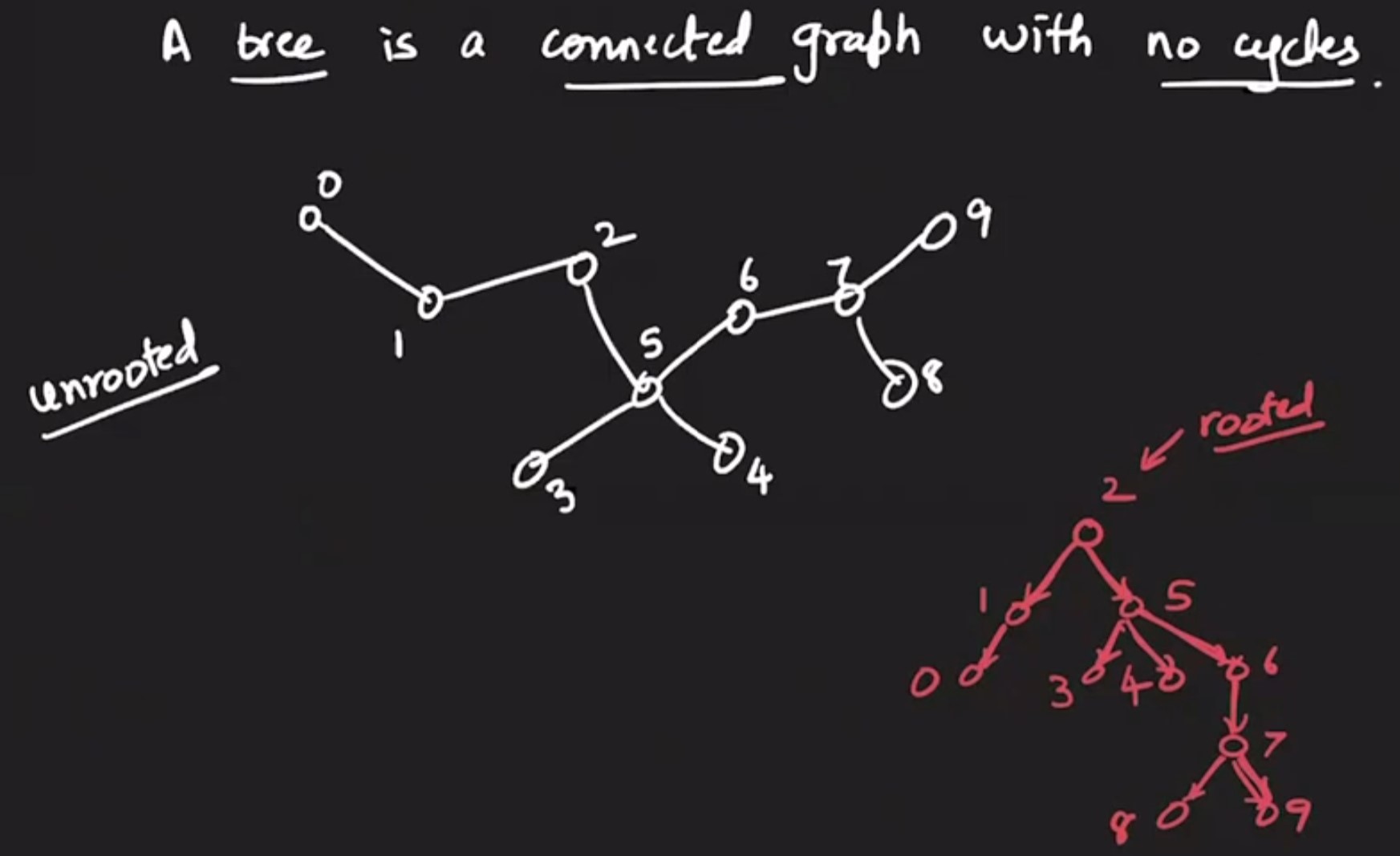
Tree is a connected graph with no cycles.
A general tree is unrooted. We can pick any node and make it a root.

Complexity Analysis

Coding Mistakes

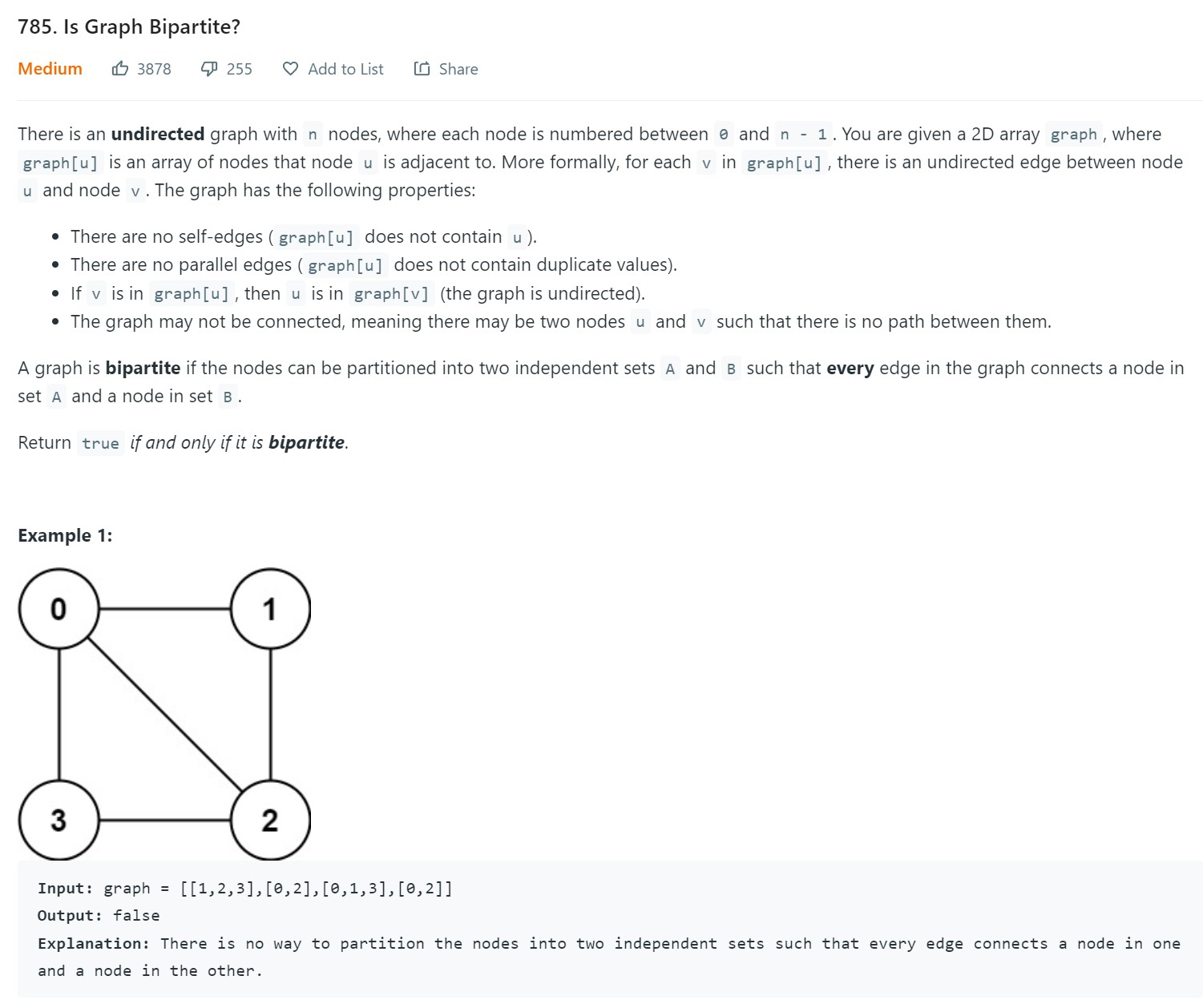
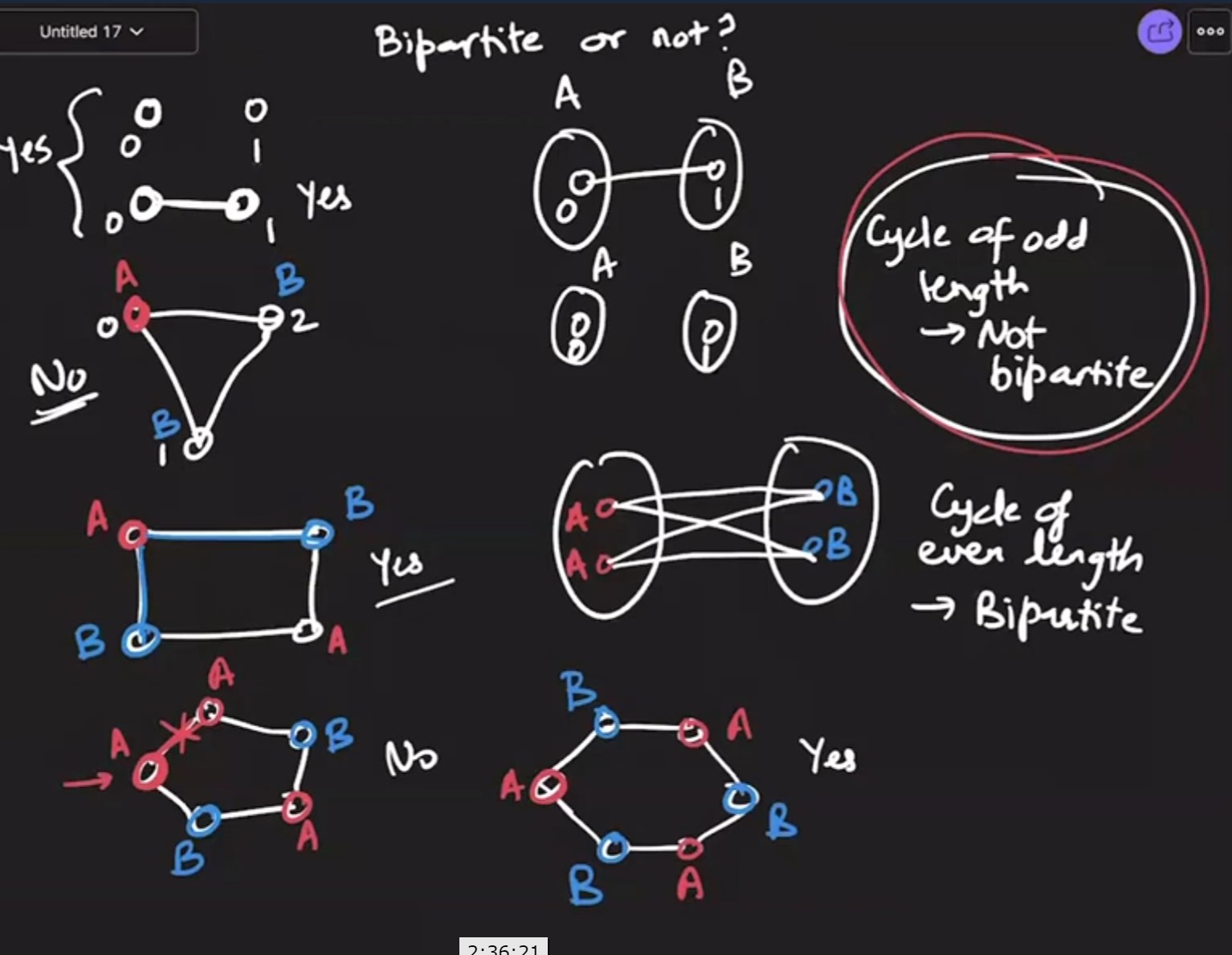
3. Is Graph bipartite? - LC 785 - Medium

Code

class Solution:
    def isBipartite(self, graph: List[List[int]]) -> bool:
	n = len(graph)
	visited = [-1] * n
	distance = [-1] * n
	parent = [-1] * n
	def bfs(node):
	    visited[node] = 1
	    distance[node] = 0
	    q = deque([node])
	    while len(q):
		node = q.popleft()
		for neighbor in graph[node]:
		    if visited[neighbor] == -1:  #First time visiting the node:
			visited[neighbor] = 1
			distance[neighbor] = distance[node] + 1
			parent[neighbor] = node
			q.append(neighbor)
		    else: # We have already seen this neighbor
			if parent[node] != neighbor: # Cycle found
			    if distance[neighbor] == distance[node]: #odd cycle found
				return False
	    return True
	for v in range(n):
	    if visited[v] == -1:
		if (bfs(v)) == False:
		    return False
	return True

Points to Note

All trees are bipartite
If the graph has cycles and it is odd, it cannot be bipartite

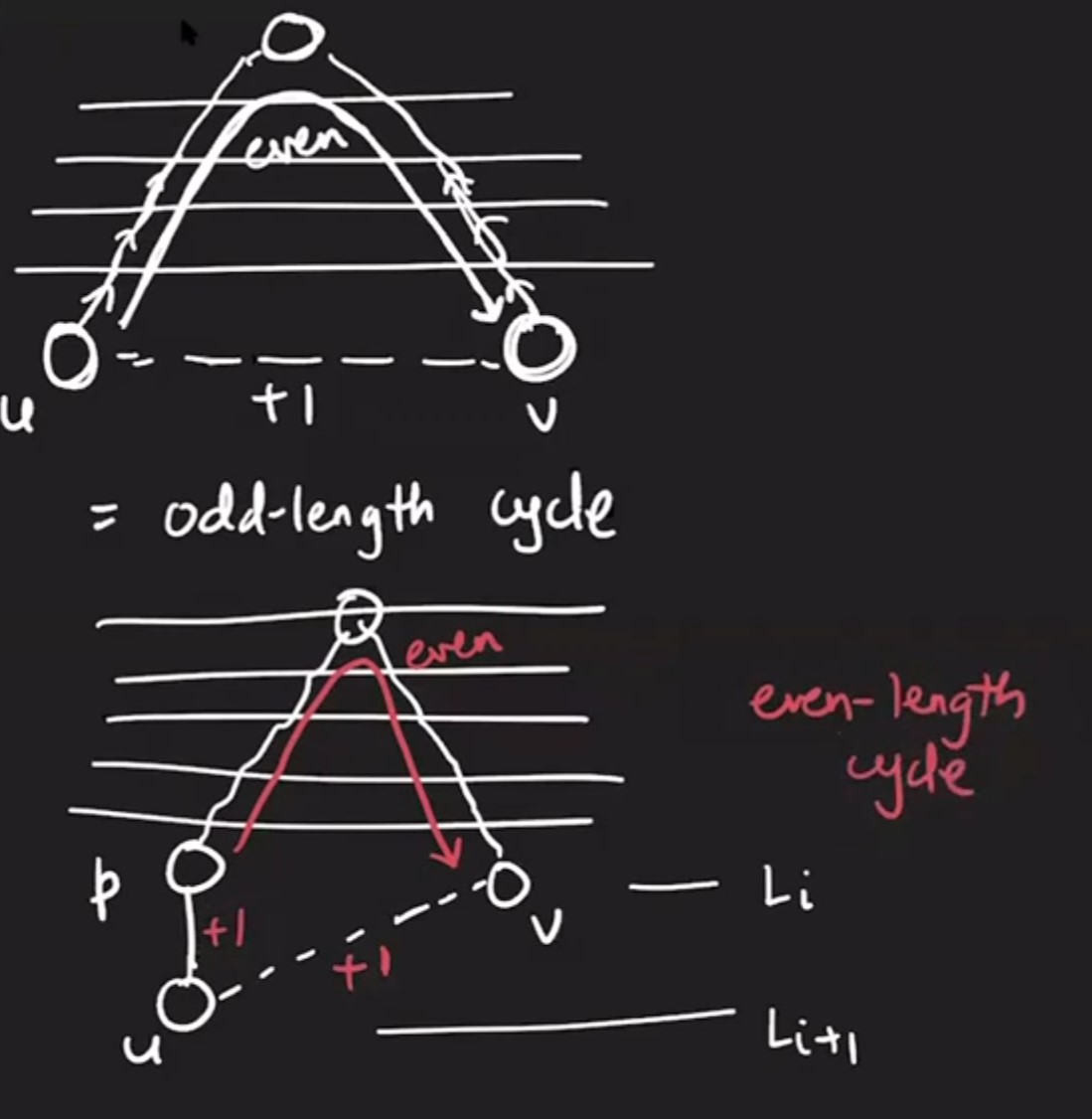
For BFS Tree:

We have to look at cross edges
Cross edges to adjacent layer is fine as it creates even length cycle and hence can be bipartite
cross edges to same layer can create odd length cycle and cannot be bipartite

Complexity Analysis

Coding Mistakes

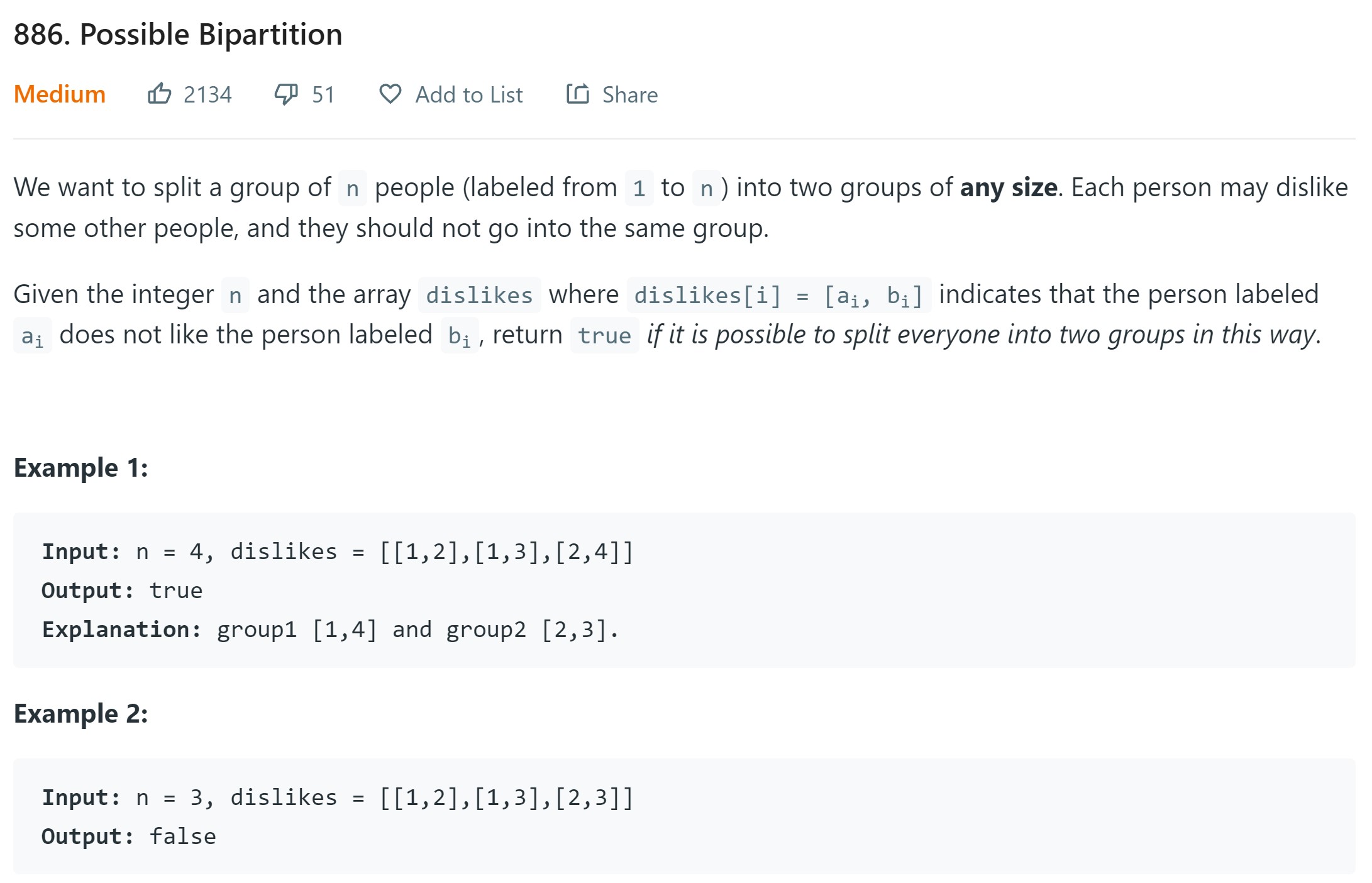
4. Possible Bipartition - LC 886 - Medium

Code

class Solution:
    def possibleBipartition(self, n: int, dislikes: List[List[int]]) -> bool:
	n =  n + 1
	adjlist = [[] for _ in range(n)]


	# Build Graph
	for (src, dst) in dislikes:
	    adjlist[src].append(dst)
	    adjlist[dst].append(src)

	visited = [-1] * n
	parent = [-1] * n
	distance = [-1] * n

	#build bfs to traverse levels
	def bfs(node):
	    visited[node] = 1
	    distance[node] = 0
	    q = deque([node])
	    while len(q):
		node = q.popleft()
		for neighbor in adjlist[node]:
		    if visited[neighbor] == -1: # Visiting the node first time
			visited[neighbor] = 1
			parent[neighbor] = node
			distance[neighbor] = distance[node] + 1
			q.append(neighbor)
		    else:  # This node was already visited. Check for cycle
			if parent[node] != neighbor: # Then we have cycle
			    if distance[node] == distance[neighbor]: #Odd length cycle found
				return False
	    return True

	for v in range(n):
	    if visited[v] == -1:
		if bfs(v) == False:
		    return False
	return True

Points to Note

Complexity Analysis

Coding Mistakes

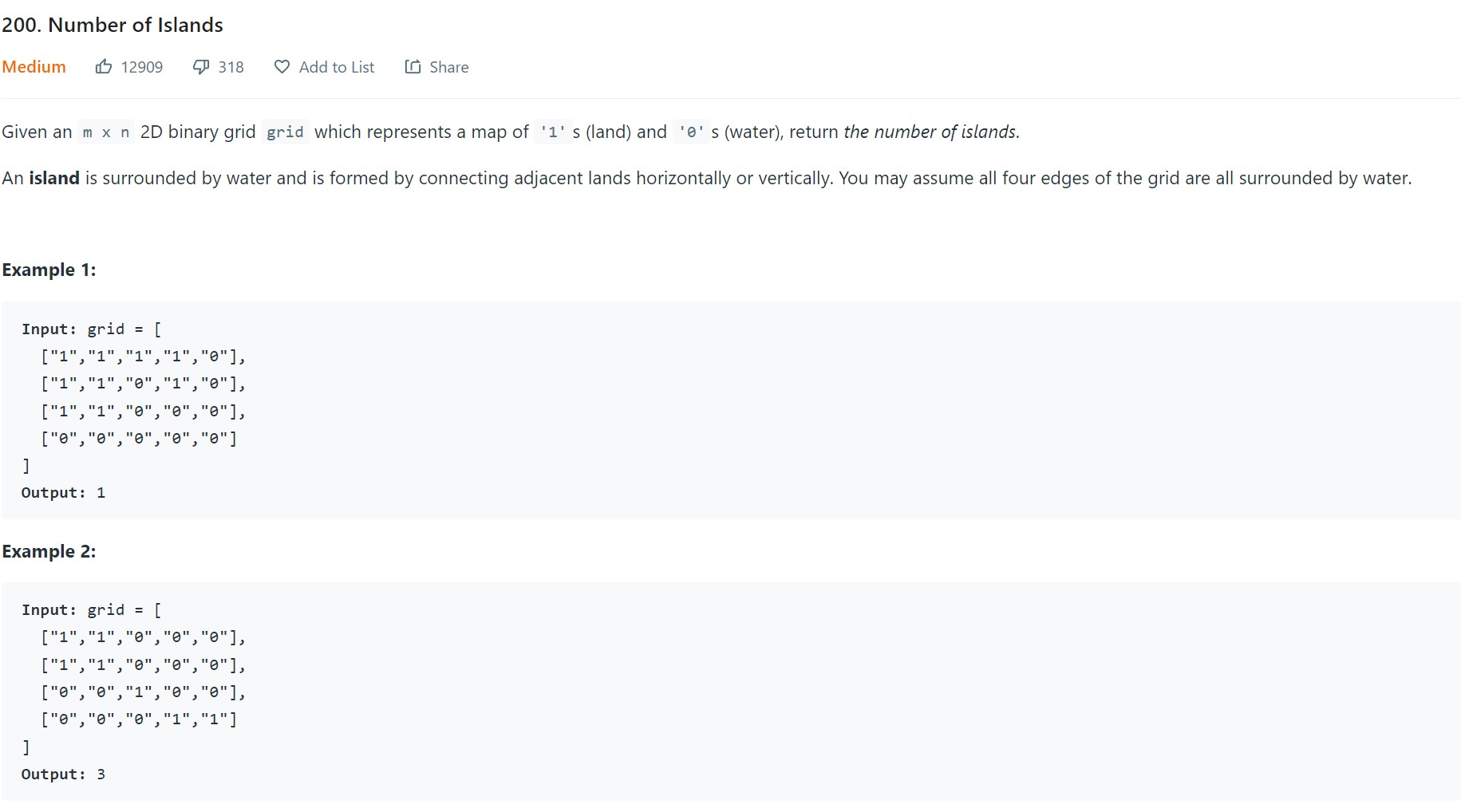
5. Number of Islands - LC 200 - Medium

Alternative Class - Graphs With Omkar: 3:48:40 hours

Code

class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
      def getneighbors(x, y):
	  result = []
	  if x+1 < len(grid):
	      result.append((x+1, y))
	  if y+1 < len(grid[0]):
	      result.append((x, y+1))
	  if x-1 >= 0:
	      result.append((x-1, y))
	  if y-1 >= 0:
	      result.append((x, y-1))
	  return result
      '''
      def bfs(i, j):
	   grid[i][j] = '0' #  Instead of visited array, we are overwriting grid directly
	  q = deque([(i, j])
	  while len(q):
	      (row, col) = q.popleft()
	      neighbors = getneighbors(row, col)
	      for (nr, nc) in neighbors:
		  if grid[nr][nc] != '0':
		      grid[nr][nc] = '0'
		      q.append((nr, nc))

      '''
      def dfs(i, j):
	  grid[i][j] = '0'
	  neighbors = getneighbors(i, j)
	  for (nr, nc) in neighbors:
	      if grid[nr][nc] != '0':
		  dfs(nr, nc)

      islands = 0
      for x in range(len(grid)):
	  for y in range(len(grid[0])):
	      if grid[x][y] != '0':
		  islands += 1
		  dfs(x, y)  # change this to dfs or bfs based on which one is enabled
      return islands

Points to Note

The hint this is a graph problem is that it indicates some kind of neighbor relationship which can potentially lead to sparse graph.
The adjlist here is 2D if we choose to represent each vertex as node in the adjlist. Similarly, visited array also has to be 2D.
Better way is to avoid creating adjlist. Edges can be represented implicitly. From row and col number of cell, we can directly infer who are its four neighbors.
Since there is no explicit adjlist, we have to call a function (say getneighbors(x, y) that will take a vertex id (row, col) and return its neighbors (max four neighbors). (x+1, y), (x,y+1), (x-1, y), (x, y-1)
The second optimization is to avoid visited array entirely. Instead, as each node is visited, change its value within the grid itself
Rest of the code structure is same as previous graph problems.
Set grid[x][y] = 0 when (x, y) is visited and not when it is captured. Otherwise, the queue size can become very large, with duplicate entries pcaked inside, and you would get a time limit exceeded issue on online coding platforms.

Complexity Analysis

Time Complexity: $O(M \times N)$

\[\begin{eqnarray} T(n) = O(V + E) \\\ = O(\text{number of cells} + \text{number of adjacent cell pairs}) \\\ = O((M \times N) +( 4 \times M \times N)) \\\ = O(5 \times M\times N) = \boxed{O(M \times N)} \\\ \end{eqnarray}\]

Note that we do not visit all the neighbors for each element. First of all, every cell need not have 4 neighbors and since we mark cells as visited, we wont visit the same cells multiple times.
Check with interviewer if overwriting the input grid is acceptable. Sometimes, they may want to preserve the input array.
Space Complexity: $O(M \times N)$ Check with IK how this is evaluated. Leetcode has many different answers

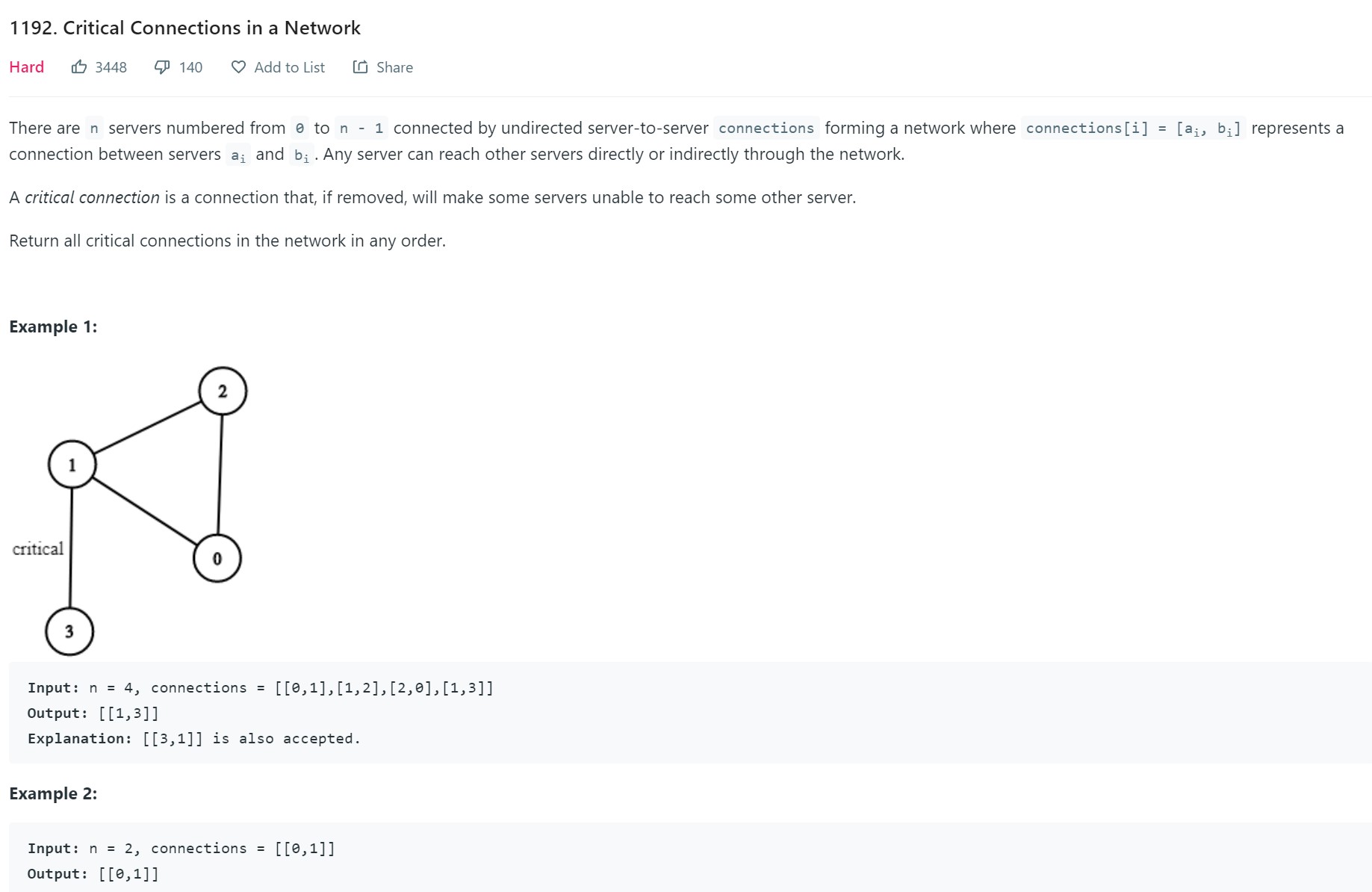
6. Critical Connections in a Network - LC 1192- Hard

Advanced Graphs Floater 1 Bridges and Articulation Points: 0:02:01 hours

Code

class Solution:
    def criticalConnections(self, n: int, connections: List[List[int]]) -> List[List[int]]:
	# Build Graph
	adjlist = [[] for _ in range(n)]
	for (src, dst) in connections:
	    adjlist[src].append(dst)
	    adjlist[dst].append(src)
	# Declare Variables
	visited = [0] * n  # To track captured/visited nodes. Since nodes can have cycles, we need to track this.
	arrival = [-1] * n  # Captures the arrival time at a given node
	start_node = [0]    # Random node to start the traversal. Typically initialized to the first one
	lowestarr = -1
	parent = [-1] * n
	result = []
	timestamp = [0]
	def dfs(node):
	    timestamp[0] += 1
	    arrival[node] = timestamp[0]
	    visited[node] = 1
	    lowestarr = arrival[node]
	    for neighbor in adjlist[node]:
		if visited[neighbor] == 0:
		    parent[neighbor] = node
		    lowestarr = min(dfs(neighbor), lowestarr)
		elif(neighbor != parent[node]): # Backedge out of myself
		    lowestarr = min(arrival[neighbor], lowestarr)

	    if lowestarr == arrival[node] and node != start_node[0]:
		result.append([node, parent[node]])

	    return lowestarr
	dfs(start_node[0])
	return result

Points to Note

Given a connected, undirected graph:
- A bridge is an edge whose removal disconnects the graph.
- An articulation point is a vertex whose removal disconnects the graph.
Example: In a computer network, bridge is a network link and an articulation point is like a router/computer in the network. If the network link is broken, all the computers connected to this network link are disconnected.
Bridges are also known as cut edges and articulation points are called cut vertex
To solve the problem, we need to check each edge and see if the graph gets disconnected. If so, then that specific edge is critical connection of the graph.
There could be more than one such critical edges in a given graph. All of them should be included in the output.

Brute Force:

Remove each edge and check if graph is connected or not via dfs or bfs.
The time complexity would be $O(m + n) * m.$
Between BFS and DFS, DFS is really useful to infer the properties of the graph. (using the arrival and departure time properties).

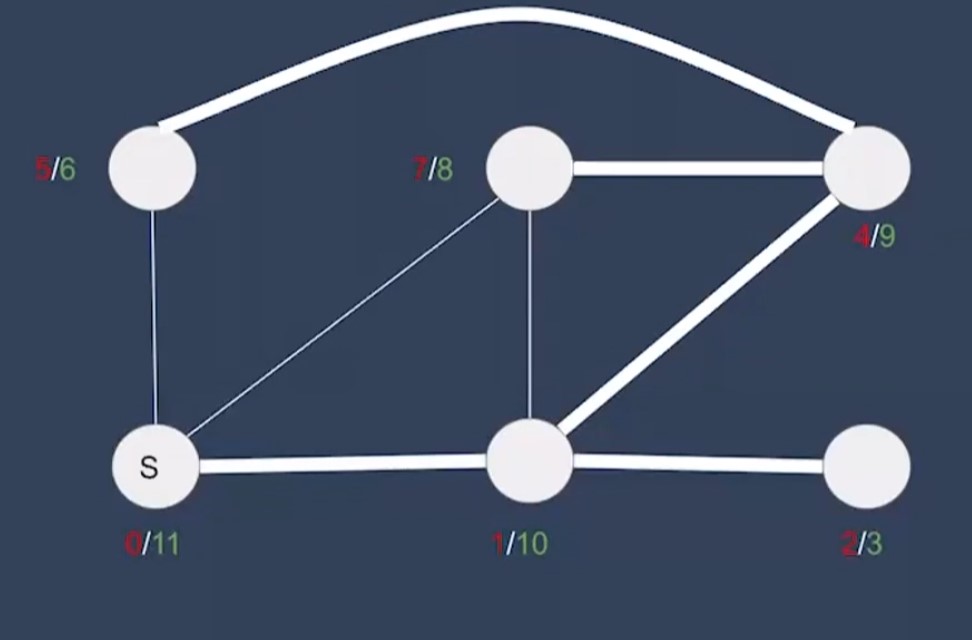
Back edges cannot create critical connections. They can create only cycles.
Cross edges are not present in undirected graphs. They are present only directed graphs.
Tree edges can be bridges. But not all tree edges need to be bridges.

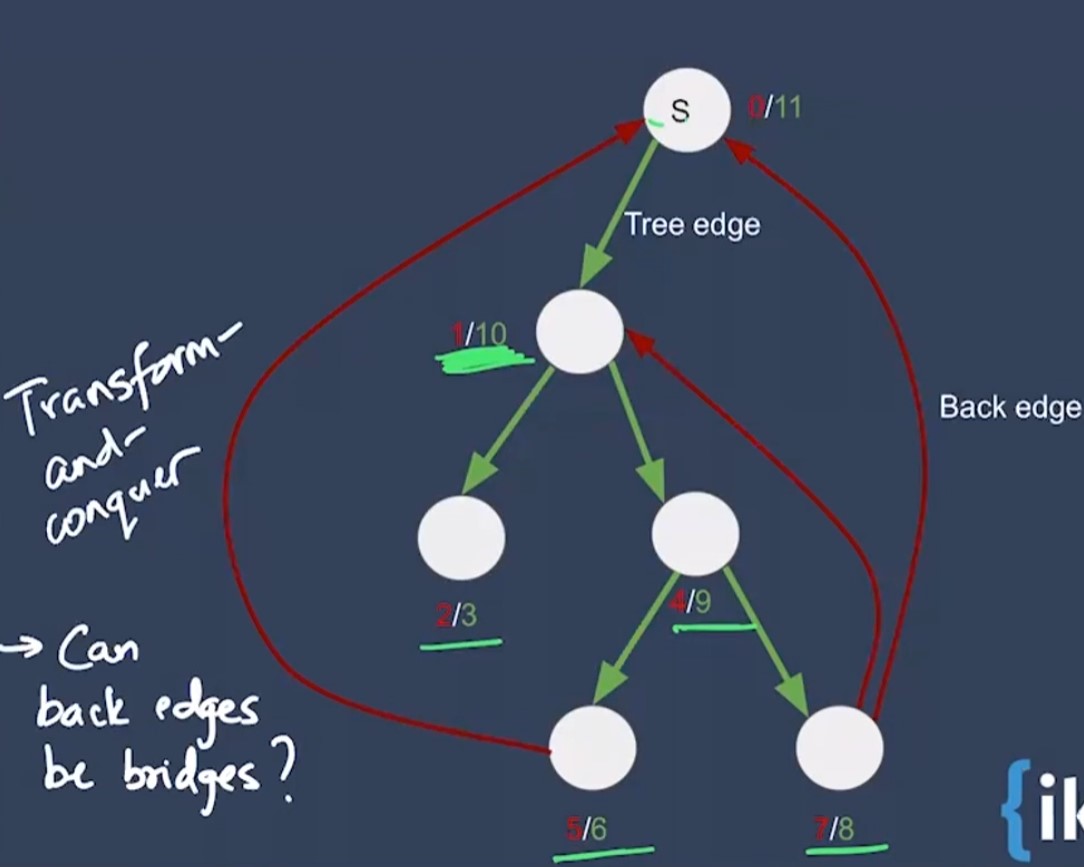
We have to find out which tree edge is a bridge? This is a local problem where each node in the subtree has to decide if the edge to its parent is a bridge. i.e if the edge to its parent is disconnected, would the subtree from that node cannot reach any of its ancestors?
To do this, we use the concept of arrival times. There could be back edges from any of the descendent nodes to any of the ancestors. So we check if the arrival time is shorter than the arrival time of the current node, then we can reach the ancestor. if so, the edge between the given node and its parent is not a bridge.

Complexity Analysis

Time Complexity: Linear $O(M+N)$

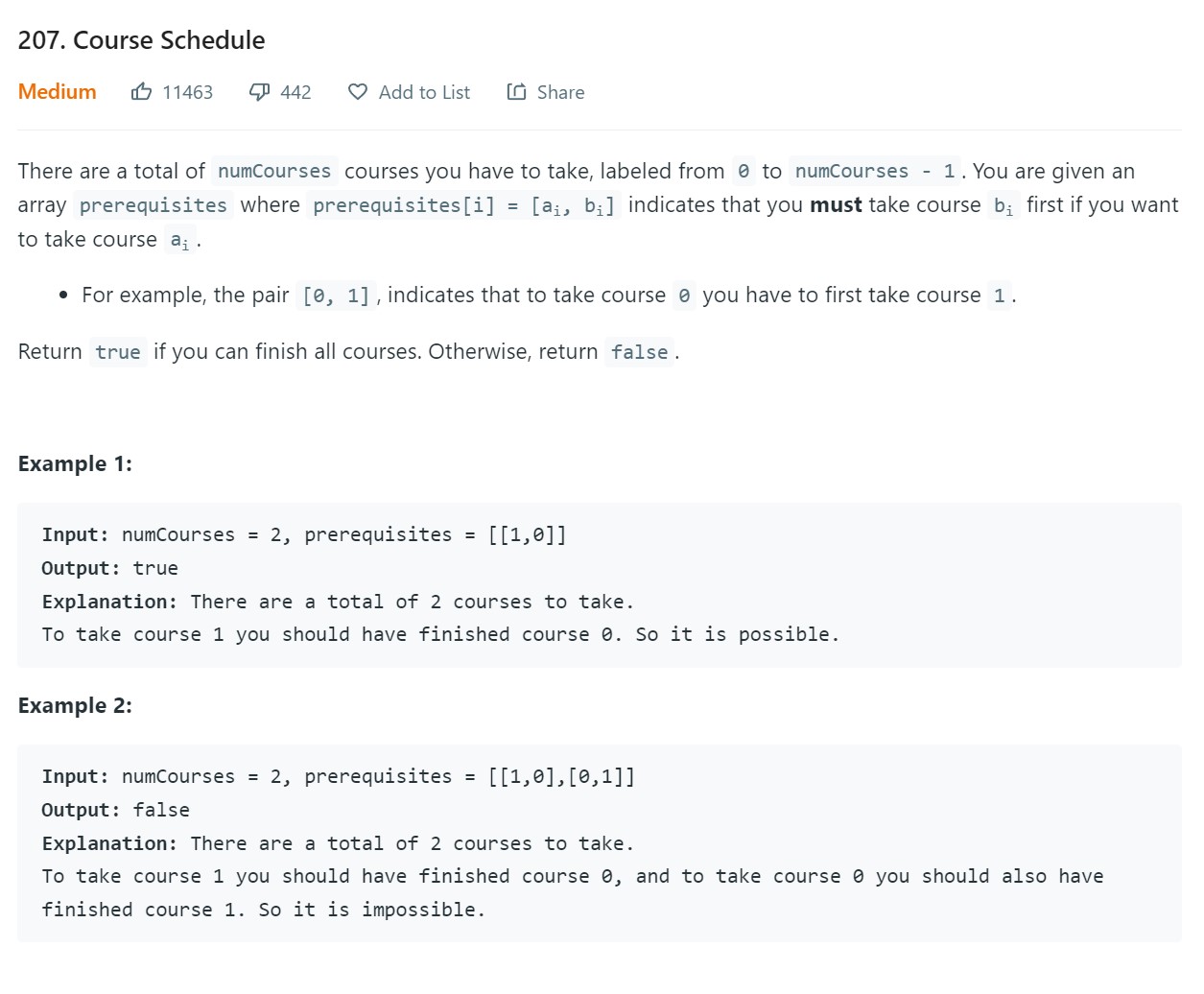
7. Course Schedule - LC207 - Medium

Code

class Solution:
    def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
      # Create an empty list for every course to track its prerequisites
      premap = {i:[] for i in range(numCourses)}

      #Fill the premap by going through all the courses and its prerequisites
      for crs, pre in prerequisites:
	  premap[crs].append(pre)

      #visitset is used to track all the courses that are
      # visited in DFS search to avoid multiple times visiting the node.
      visited = set()

      def dfs(crs):

	  # If we are going to back to a node that is already visited,
	  # it means there is a loop. Return False.
	  if crs in visited:
	      return False

	  if premap[crs] == []:
	      return True
	  # We are currently visiting this course. add it to visited set
	  # and recursively call its prerequisites
	  visited.add(crs)
	  for pre in premap[crs]:
	      # If one course cannot be completed and
	      # identified a loop, then we cannot complete all the courses.

	      if not dfs(pre):
		  return False

	  # Now we need to remove it. Why? we are no longer visiting.
	  # We finished visiting it. If we do not clear it, the test cases do not pass
	  visited.remove(crs)

	  # We do this because if we have to ever run dfs search again for this course,
	  # it will return True instead of running the entire function.
	  # Otherwise time limit exceeded can happen.
	  premap[crs] = []

	  return True # all courses can be completed

      # We are looping like below because graphs can be disconnected. Example:
      # 1 --> 2
      # 3 --> 4
      for crs in range(numCourses):
	  if not dfs(crs):
	      return False
      return True

Points to Note

Explain the problem in own words:

Some courses have prerequisities. Is it possible to finish all the courses given the prerequisites.
if a course does not have any prerequisite, we can complete the course.
if a course has a prerequisite, and if the prerequisite can be completed, then the course can be completed.
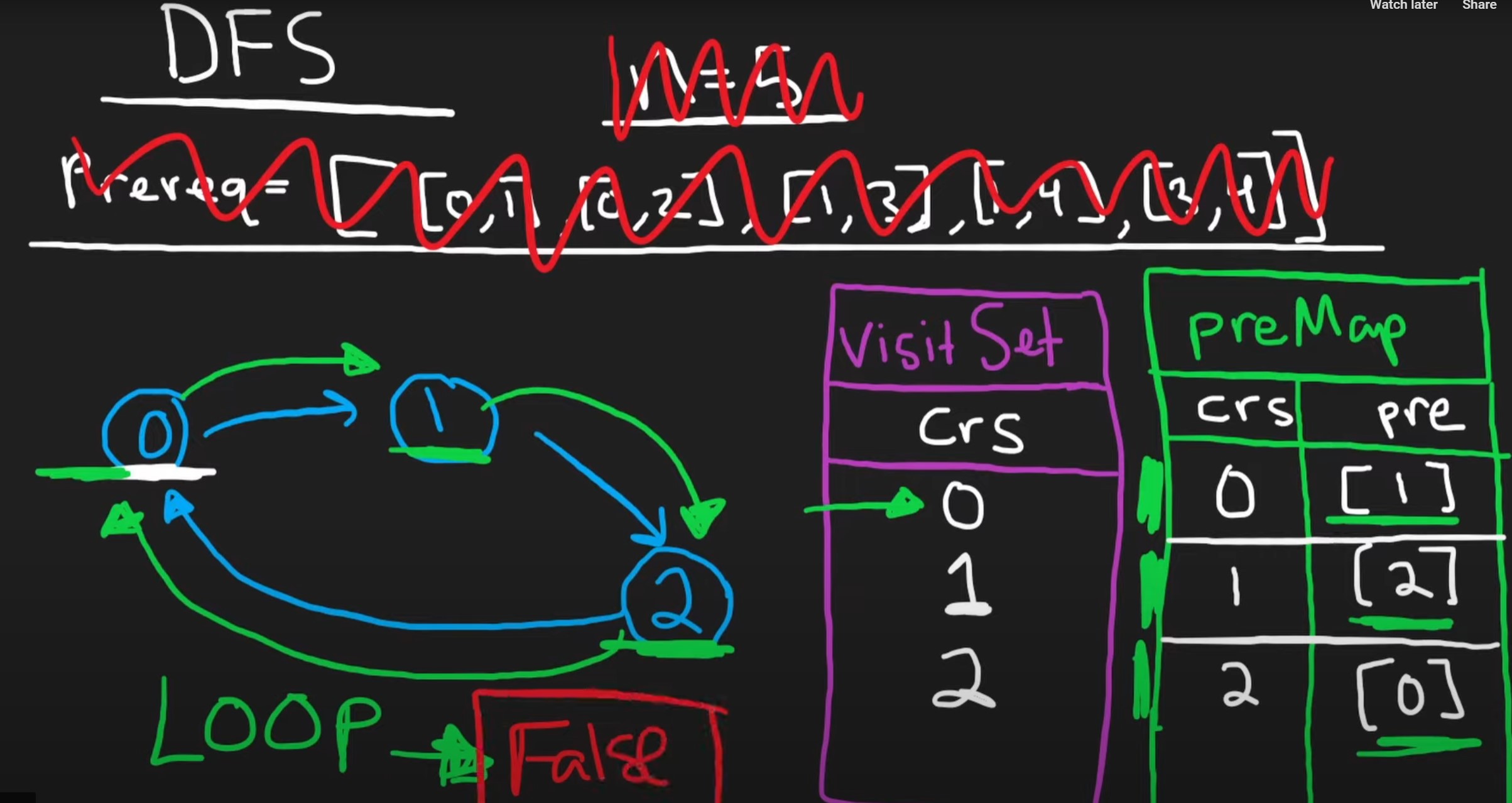
When is it impossible to finish a course? If a course has prerequisite and the prerequisite points back to the course as its prerequisite, then there is a cycle and this means we cannot complete neither of the courses.

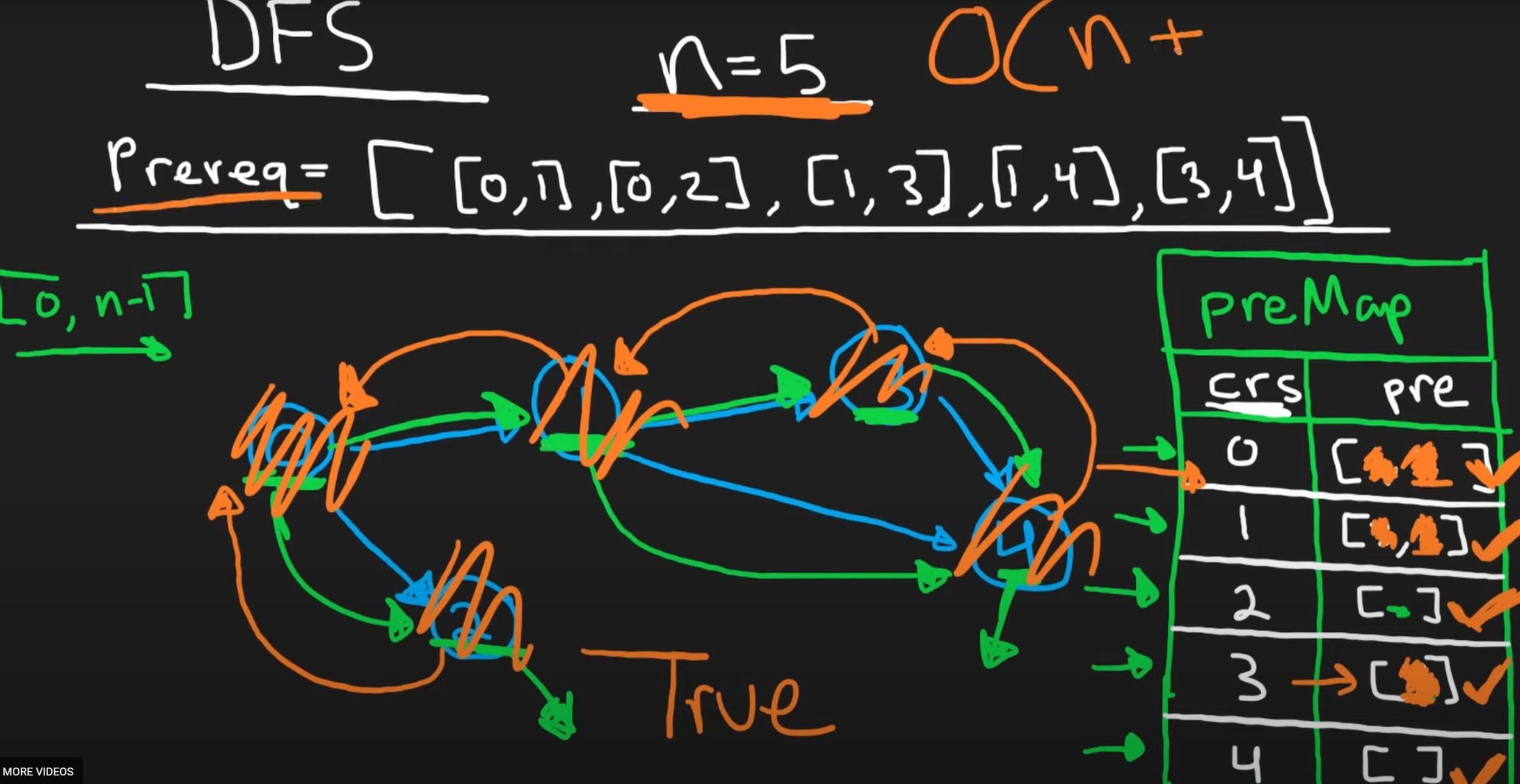
Propose solution approach:

Both DFS and BFS can be used to solve this.
Start from any course. and look for its prerequisite in recursively until we reach a course which does not have any prerequisite.
For this keep a hashmap where each course is the key and its prerequisites the list of values.
Run the DFS recursively from 0 to n-1. For each node, look up the hashmap and recursively call it.
Once a course which does not have any prerequisite is identified, we know it can be completed.
Remove the prerequisities from each node once recursively we find that they further point to other prerequisites which can be completed.
Thus if we can complete every course, return True else False.
How do we detect a cycle or loop of prerequisite? We can use an array or set that tracks which courses we are visiting along with the DFS search.

Complexity:

Time Complexity:

N is the number of nodes and P is the number of prerequisities which are the edges. So $O(N + P)$
It would take us $|P|$ time complexity to build a graph in the first step.
Since we perform a postorder DFS traversal in the graph, we visit each vertex and each edge once and only once in the worst case, i.e. $O(N + P)$

Space Complexity:

A graph data structure which would consume $O(N + P)$ space
visited set takes $O(N)$ space
The recursion call stack space in the worst case will have all the nodes chained up in a line and it will be $O(N)$.
Total Space Complexity = $O(N + P) + O(N) + O(N) = O(N + P)$

8. Course Schedule II - LC 210 - Medium

Code

class Solution:
    def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:

	#build adjacency list of prereqs
	prereq = {c:[] for c in range(numCourses)}

	for crs, pre in prerequisites:
	    prereq[crs].append(pre)

	# A course has 3 possible states:
	# visited: course has been added to output
	# visiting: course not added to output, but added to cycle
	# unvisited: Course not added to output or cyle

	output = []
	visited, cycle = set(), set()

	def dfs(crs):
	    if crs in cycle:
		return False

	    if crs in visited:
		return True

	    cycle.add(crs)
	    for pre in prereq[crs]:
		if dfs(pre) == False:
		    return False

	    cycle.remove(crs)
	    visited.add(crs)
	    output.append(crs)
	    return True

	for crs in range(numCourses):
	    if dfs(crs) == False:
		return []
	return output

Points to Note

Explain the problem in own words:
- Check if it is possible to take all the courses with the prerequisites.
-If yes, return the order of the courses. If not, return empty set.
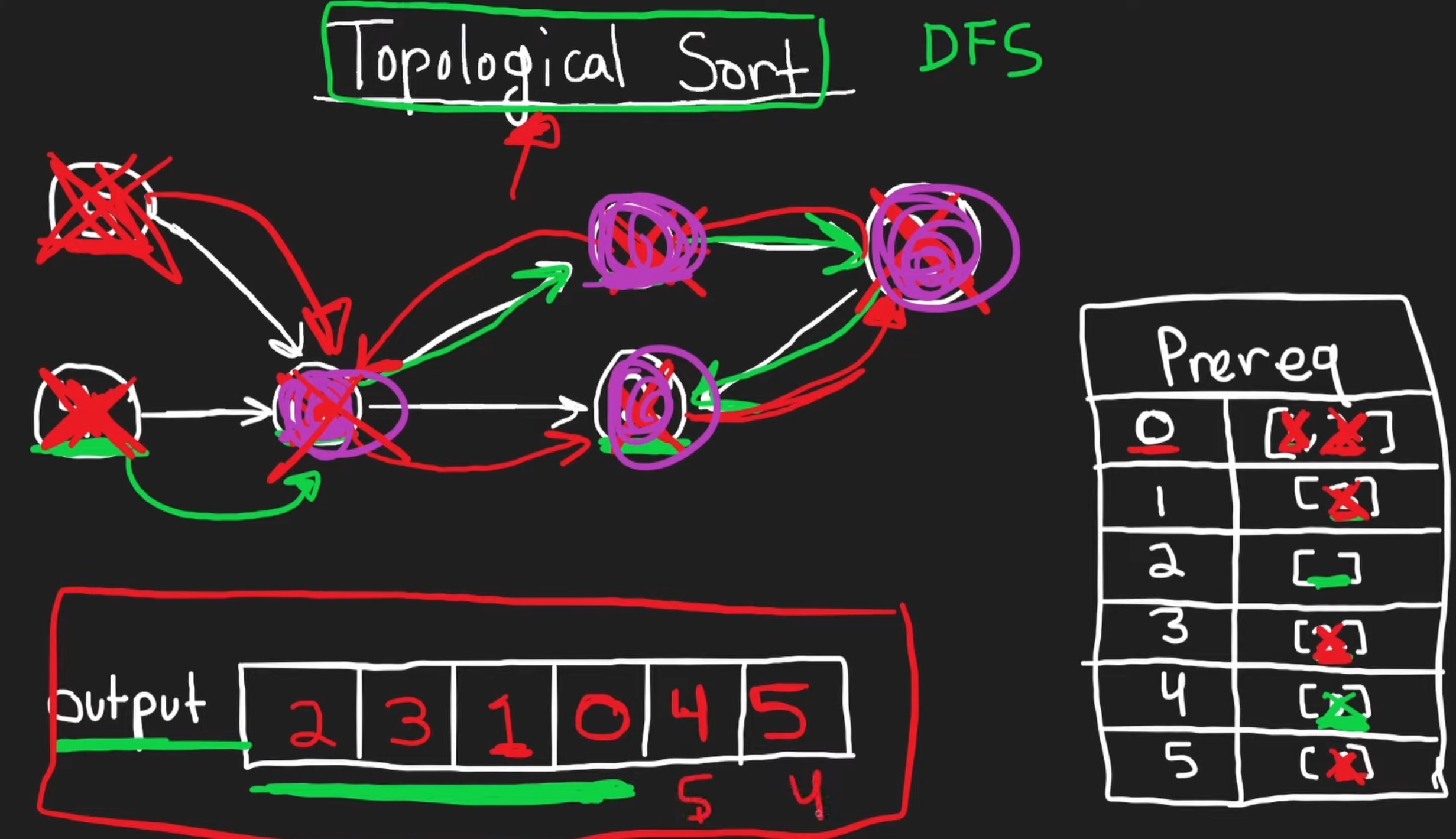
Propose solution approach: -Approach is to use topological sort. Starting from a node, we run dfs. To do this, build adjacency list of prereq.
- Create a prerequisite map which has info. for each node its prerequisites
- The output should be the order in which the courses can be taken.
- Start at a node, identify its prerequisites, go to one of them and check recursively if it has its own prereq.
- Traverse until a course has no prerequisite. Add it to the output. Cross it out as we never have to visit this node again.
- Backtrack and add the courses that have prereq which has been already added to the output.
- Return empty list if cycle is detected and in this case topological sort is not even possible.
- A cycle is identified by using a hashset and remembering the path that was traversed earlier.

Complexity:

Time Complexity:

N is the number of nodes and P is the number of prerequisities which are the edges. So $O(N + P)$
It would take us $|P|$ time complexity to build a graph in the first step.
Since we perform a postorder DFS traversal in the graph, we visit each vertex once and each edge once at most twice in the worst case, i.e. $O(N + P)$

Space Complexity:

A graph data structure which would consume $O(N + P)$ space
visited set takes $O(N)$ space
cycle set takes $O(N)$ space
The recursion call stack space in the worst case will have all the nodes chained up in a line and it will be $O(N)$.
Total Space Complexity = $O(N + P) + O(N) + O(N) + O(N) = O(N + P)$

Solutions by type

References:

Omkar Slides:

Alternate Class Graphs - Omkar Slides

trees BFS DFS

Last updated on Mar 16, 2020

Edit this page