Notes from Graph foundation videos:

What is a graph?:

Term	Definition
Node or Vertex	The entities in the graph
Edge	The line that connects two adjacent nodes.
Adjacent Nodes or Adjacent Vertices	The nodes/vertices directly connected via edge
PATH	Sequence of adjacent vertices
Degree of Node	The number of edges connected or incident on node is called degree of Node. Edges that flow into vertex is indegree and the edges that go out of the node is called out degree
Cycle	If we start from a node and follow edges that bring back to the same start node, then those vertices/nodes form a cycle. An undirected graph with cycle is called undirected cyclic graph
Connected graph	Every node in the graph connected to every other node via a series of edges. If there is no path to a given node, then it is a disconnected graph
DAG	Directed Acyclic Graph enforces a precedence order on the nodes in the graph. Eg. Scheduling tasks. Certain tasks can be addressed after completing some other tasks. Neural network is a DAG
Tree	A tree is a connected graph with no cycle.
Binary tree	A special case of a tree where each node has exactly two or fewer children
Forest	Set of disjoint trees (tree with disconnected nodes)

Degree of vertices:

• Degree of vertices: in an undirected graph is the number of vertices adjacent to the vertex. or the number of edges that stick out of the given vertex to other nodes.

• Multi Graph - If there are more than one direct edge or path between two vertices or if there is self loop. A path that starts from the node and ends within it.

Sum of the degrees of vertices:

Graph is represented as G = (V, E) where V is the number of nodes and E is the number of edges.

Undirected Graph

Directed Graph

• In directed graphs, the degree of a node is distinguished as indegree and outdegree.
  • Indegree - # of edges coming into the vertex
  • Outdegree - # of edges going out of the vertex

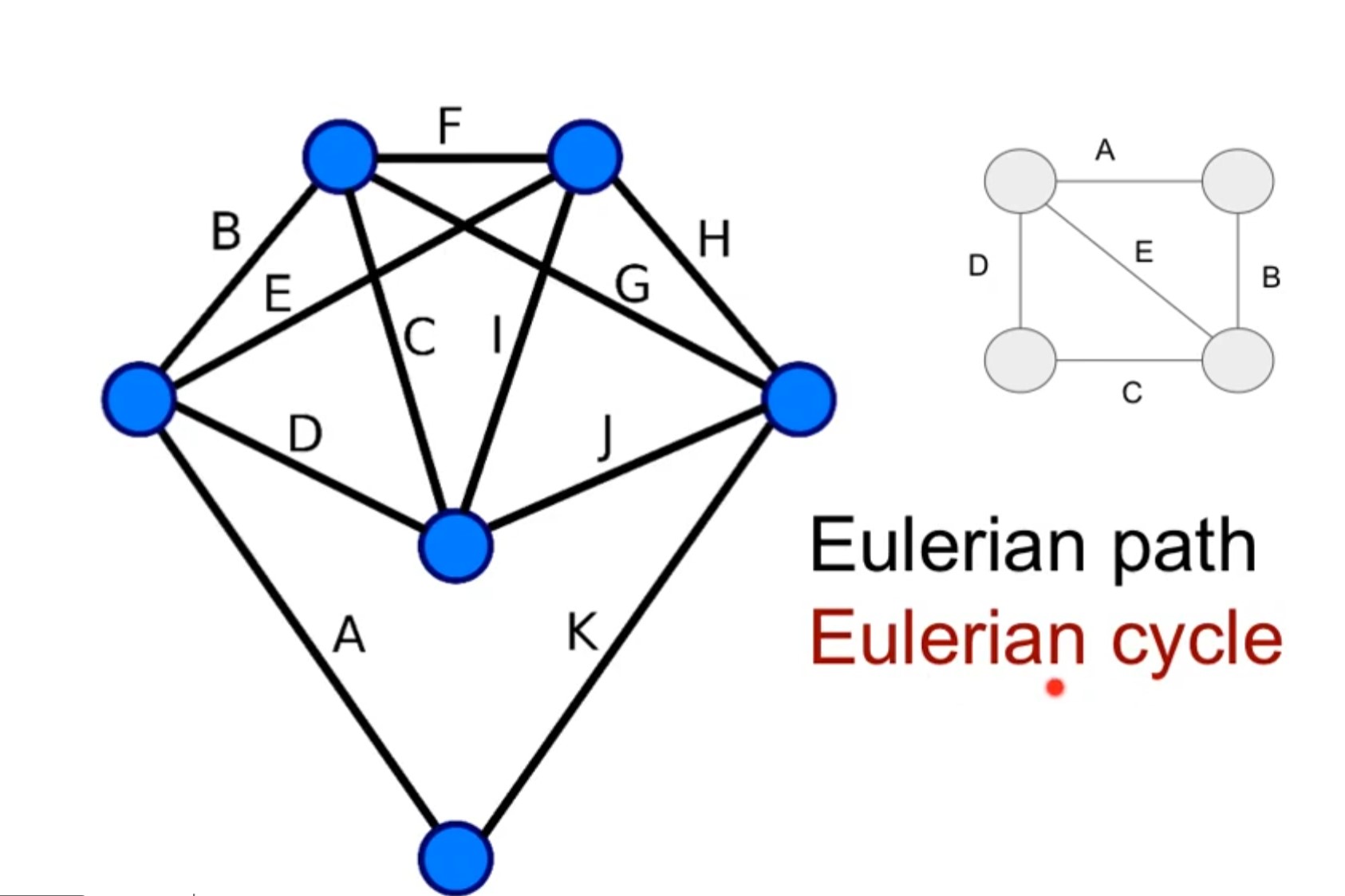
Modelling Eulerian Cycles:

• If the given undirected graph has any cycle that covers each edge exactly once and comes back to starting point is Eulerian Cycle.

• We can have non cyclical path whcih also traverses all path exactly once. It may end up some where else than starting point as it is not cycle and it is called Eulerian path. Every Eulerain cycle is eulerain path but it is not vice versa.

• Finding eulerian cycle and eulerian path problems are slightly different.

Formulating the problem as Eulerian cycle is important. Otherwise it could possiblly end up as Hamilton cycle which is NP hard problem? Example Problem: Assume you are in front of the museum. You need to visit all the paintings on all the walls and come back to the entrance without revisiting a wall twice. To solve this problem, ask if this has a eulerian cycle? If so, we can do this. To frame this problem, treat every wall as the edges and the corner between walls as modelled as vetrices. If the problem is framed the other way, every wall is vertex and the corners as the edges, then it becomes Hamiltonian Cycle Problem which is NP hard and there is no known polynomial time algorithm It matters how a problem is modelled as graph problem.

• Eulerian cycle does not mean the graph has to be connected. The graph could be unconnected graph but the edges have ot be connected in the connected component to ensure it has eulerian cycle.

Even Edges

• Eulerian cycle assumes that no edge or path is used twice. This means, every vertex that is entered should be exited through a different path. THis means, vertex should have even degrees.
  • If the vertex has odd degree, then there is no eulerian cycle in it.

How to check fi a graph has eulerian cycle?

• Confirm vertices have even degrees
• Start a random walk and when coming back to the same vertex, backtrack and go back to a vertex which has unused edges and do mini walk using one of the unused edges.
• Keep repeating this process until all the unused edges are covered.

Given an undirected graph that is connected, if degrees of eveyr vertex is even it has eulerian cycle.

Eulerian Path

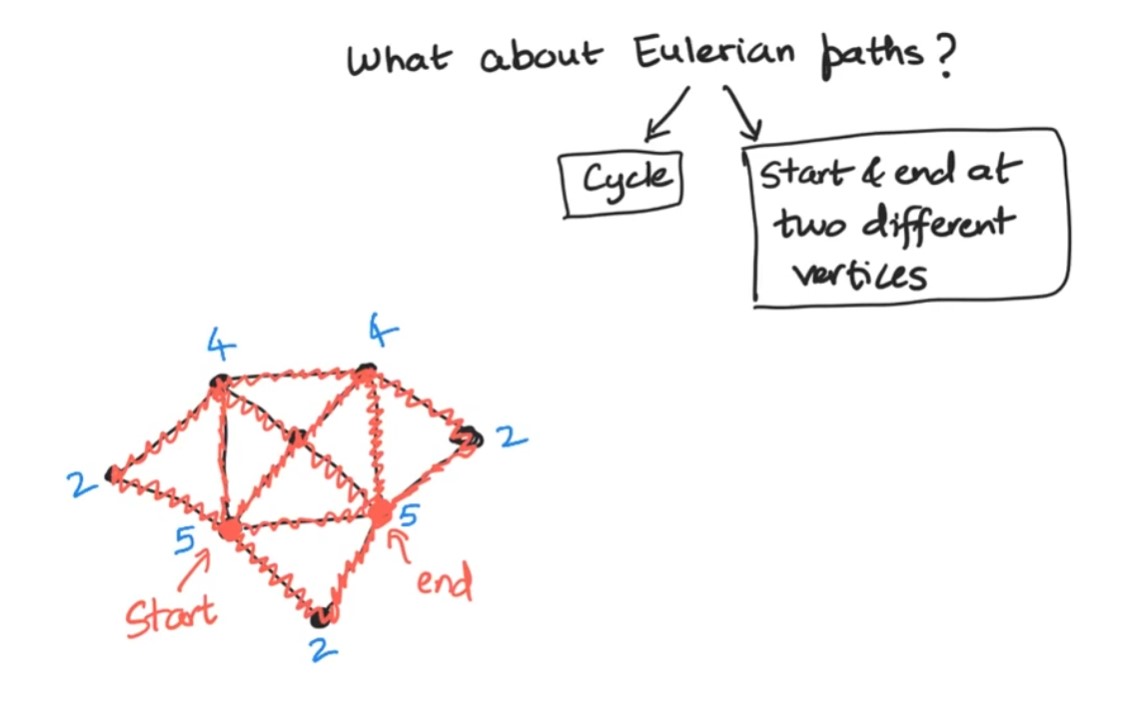
Keeping the discussion only to connected graphs, a graph can have eulerian path either if it has eulerian cycle or if the start and end vertex are different. For this to happen, all the intermediate vertices should have even degrees as the entry and exit should be using different path but the start and end vertex can be odd because from start vertex we start but need not end up there but could end up in a different vertex.

Every graph with 2 vertex of odd degree can have eulerian path. This can be proved by adding a new path between the two vertices having odd degrees to make them even and this will result in Eulerian cycle. If we remove this newly added edge, it results in Eulerian path. So it confirms if a graph has two vertices with odd degrees and rest are even, then it has Eulerian Path.

Odd Degree of vertex

In a connected undirected graph, can a single vertex can have an odd degree? No. Sum of degrees of vetrices = twice of number of edges = even number even + odd = odd so this is not possible. Extending thislogic, 3 vertices or 5 vertices or any odd number of vertices cannot have odd degrees.

• If a graph has 0 vertex of odd degree - Eulerian cycle
• if a graph has 2 vertex of odd degree - Eulerian path (start and end vertex can have odd degree)
• if a graph has 4 or 6 or any other even number of vertices having odd degree, it can neither have eulerian cycle nor eulerian path.

Graph Representations: n = |v| number of vertices m = |e| number of edges

4 different ways of representation:

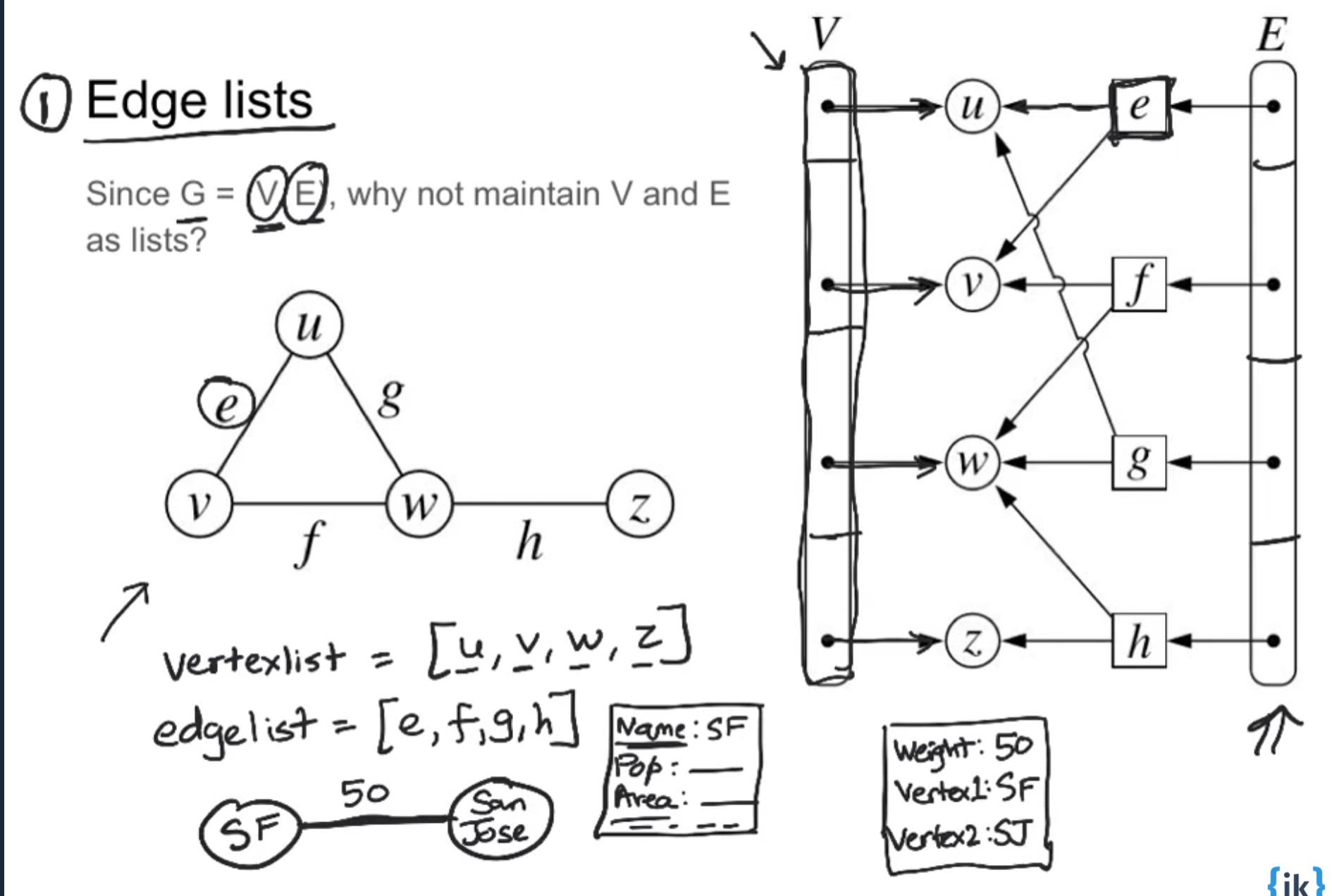
1. Edge List

   • Maintain vertices and edges as list

   • References to vertex objects are maintained in an array if the vertex is simple positive integers else in hashtable.

   • Vertex object can have attributes like vertex name, vertex id etc.

   • References to edge objects are maintained in an array or linked list.

   • The edge objects can have info. like weight, or cost of the edge, vertex names that are connected by the edge and so on.

Time Complexity: Given a graph and if the question is to find all the neighbors of all the vertices, if the graph is represented as edge list: For n vertices, any two vertices can have an edge this means it is C(n,2) n choose 2 = n(n-1) / 2 = O(n^2)

IN graph traversal, edges can be much more than nodes and the graph time complexity is measured by the time for traversing edges or how edges are represente.d The four representations are basically how edges are represented and not about vertices.

To explore grpah and discouver its tructure by starting at a vertex and go to its neighbors and do the same for each neighbors, in edgelist, we have to traverse the whole list an dsee which edges mention the vertex and then look at the other end points of the vertex which is its neighbors. = O(|E|) or O(m). if we have to do for every vertex in teh graph then it is O(mn) since m can be n^2, O(mn) can be at worst case O(n^3).

Space complexity of edge list is O(m) + o(n). Each vertex takes constant amount of stroage and there are n verttices Each edge takes constant amoutn of storage and there are m edges.

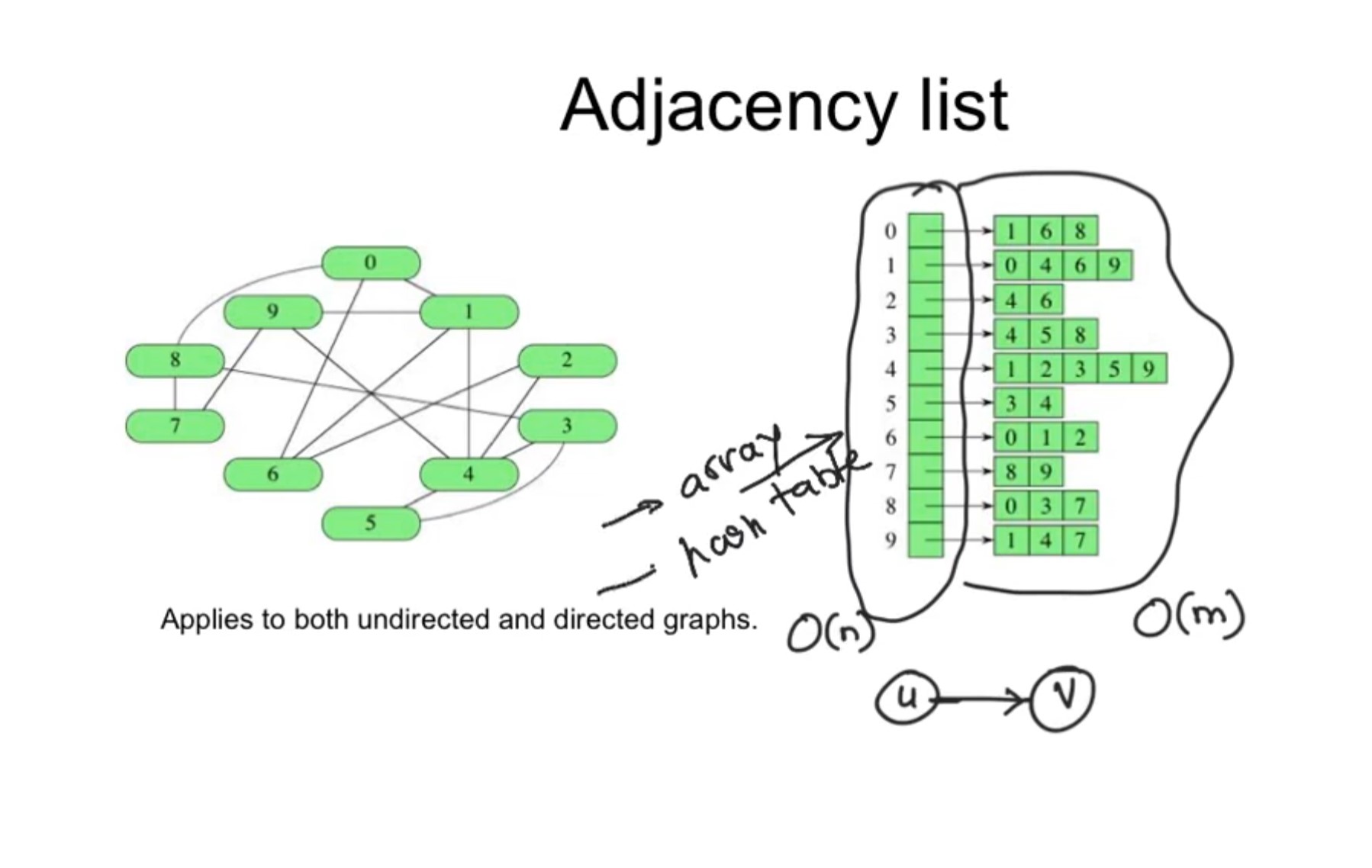
1. Adjacency List: It is very costly to store all the edges in a single global unsorted list, in this representaiton , each edge is stored with its end point vertices. By looking at the id of the vertex, we get all the neighbors of the vertex. The time is euqal to the degree of the vertex.

   • This applies to the directed and undirected graph.

   • Vertex info. or attributes are stored separetly for all the representations. Only the edges differ in the representations. So there is additional O(n) space is used for vertices.

   • IN some cases hashtable can point to vertex object which has an attribute to the adjacency list of the vertex. This is called objects and pointer approach. An exmaple is if the graph is used for both road network and airlines network, the cities remain the same, (vertex) the edges (routes) are different.

   In undirected graph, a graph is represnted twice in the list (for each of the two vertices)

Pseudocode

#only for connected graph
  class Graph:
    adjlist []
    numofvetrices

  def addEdge(u, v, undir=True):
    adjist[u].add(v)
    if undir == True:
     adjlist[v].add(u)

  bool haseulireanpath()
  {
  odd = 0
  for vertex in adjlist:
    if (adjlist[vertex].size() % 2) == 1:
      odd += 1

  if odd == 0: eulerian cycle and eulerian path
  if odd == 0 or 2, eulerian path
  else return False

• Accept size as parameter while creating Graph object.

• Then initiatlize the adjlist for the size.

• Adjacenty Matrices:

  • In adjacency metrics, an n by n matrix is created (n is the number of vertices) initialized to zero and for the edges associated with the vertex, this is flipped to 1. if vertex i has an edge to vertex j, then row i, column j is set to 1 and for undirected graph, row j col i is also set to 1.
  • For undirected graph, the matrics will be symmetric.. the diagonal will be all zero.

 Time complexity:

to find all neighbors of all vertex is to go to the given row and scan the entire row to find the neighbors. For any vertex to find neighbors is O(n) space compleixty is O(n^2) and is fixed.

• This graph is useful only for dense graph where there are lots of edges…It is better to store bit array to store the matrix so that only single bit is used to track if edge exists.

• For sparse graph (# of edges is much lower than V^2) It is nowhere close to square of the vertices.

• Facebook or social graph has 2 billion users so 2 billion vertices but on average every person has just a fwe hundred friends. In this case, the # of edges is fractional of the #of vertices. Here adjacency matrix will be very large.

• How do we say if there is an edge between u and v. If this is required frequnently, then adjancey matrics is useful. Most of the sparse metrics use adjanccey list and not matrics.

• IN adjacency matrix, instead of storing 1, we can store the weight or distnace value in the matrix.

• In the adjancey list, we will store the weight in the hashtable (instead ofs toring single id, we store vetex id and weight) a list of pairs instead fo just vertex id.

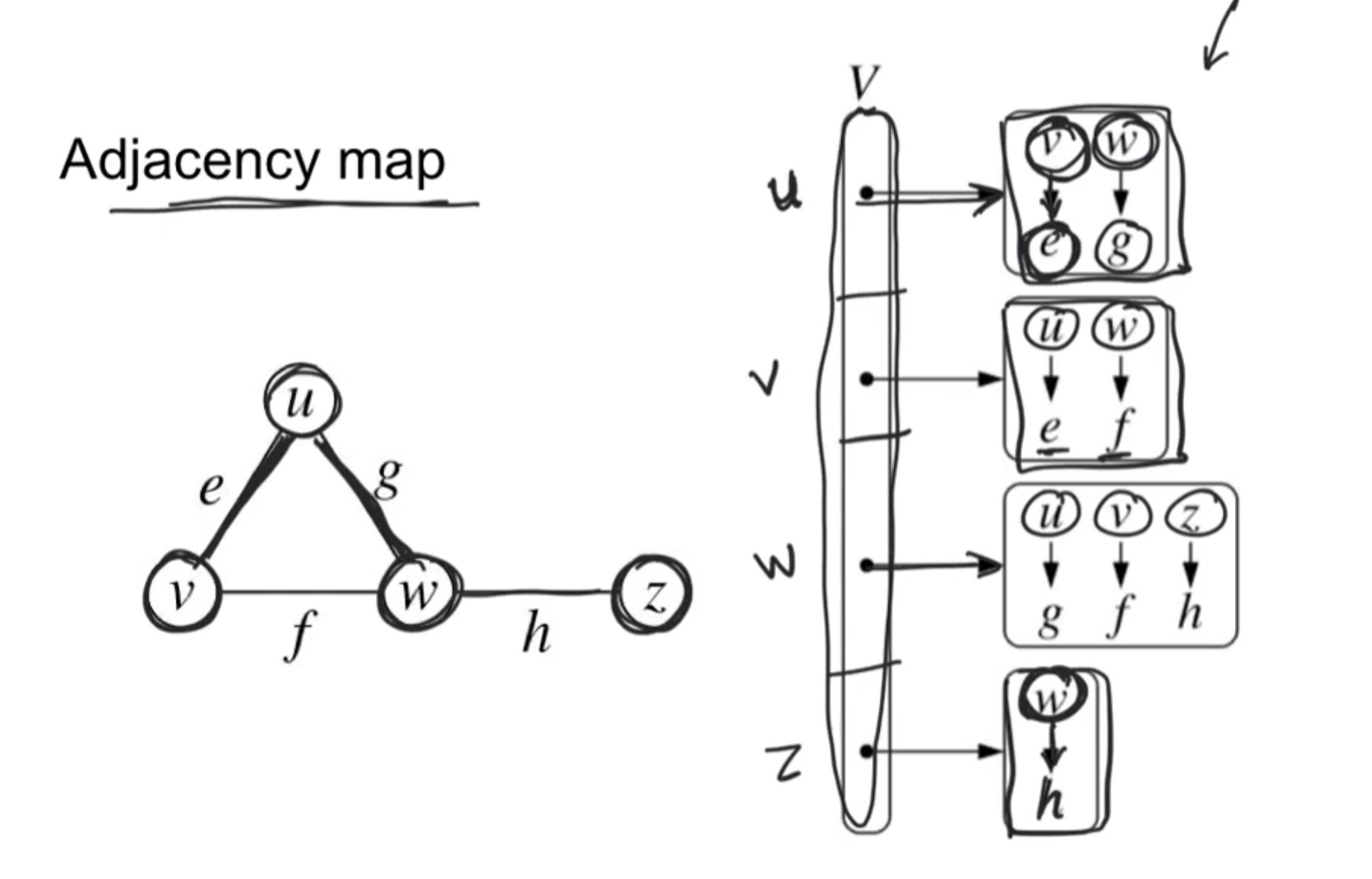
1. Adjacency Map:
   • This representation stores a hashmap or dictionary of key value pairs of neighbors and the edge value.
   • Each vertex points to a hashmap entry that contains the key value pairs of its neighbors.
   • This representation effectively combines the space requirements of adjacency list and time requirements of adjacency matrix.

Implicit representations of Edge:

• In grid like structures, we can dynamically calculate the neighbors as need arises without sacrificing time and no need for adjacency list or maps. (these are special case problems)

Notes from Video: General Graph Search:

Even if the vetrices have even degrees, if the graph is not connected, then it will not have eulerian cycle or path. So first step is to check if graph is connected.

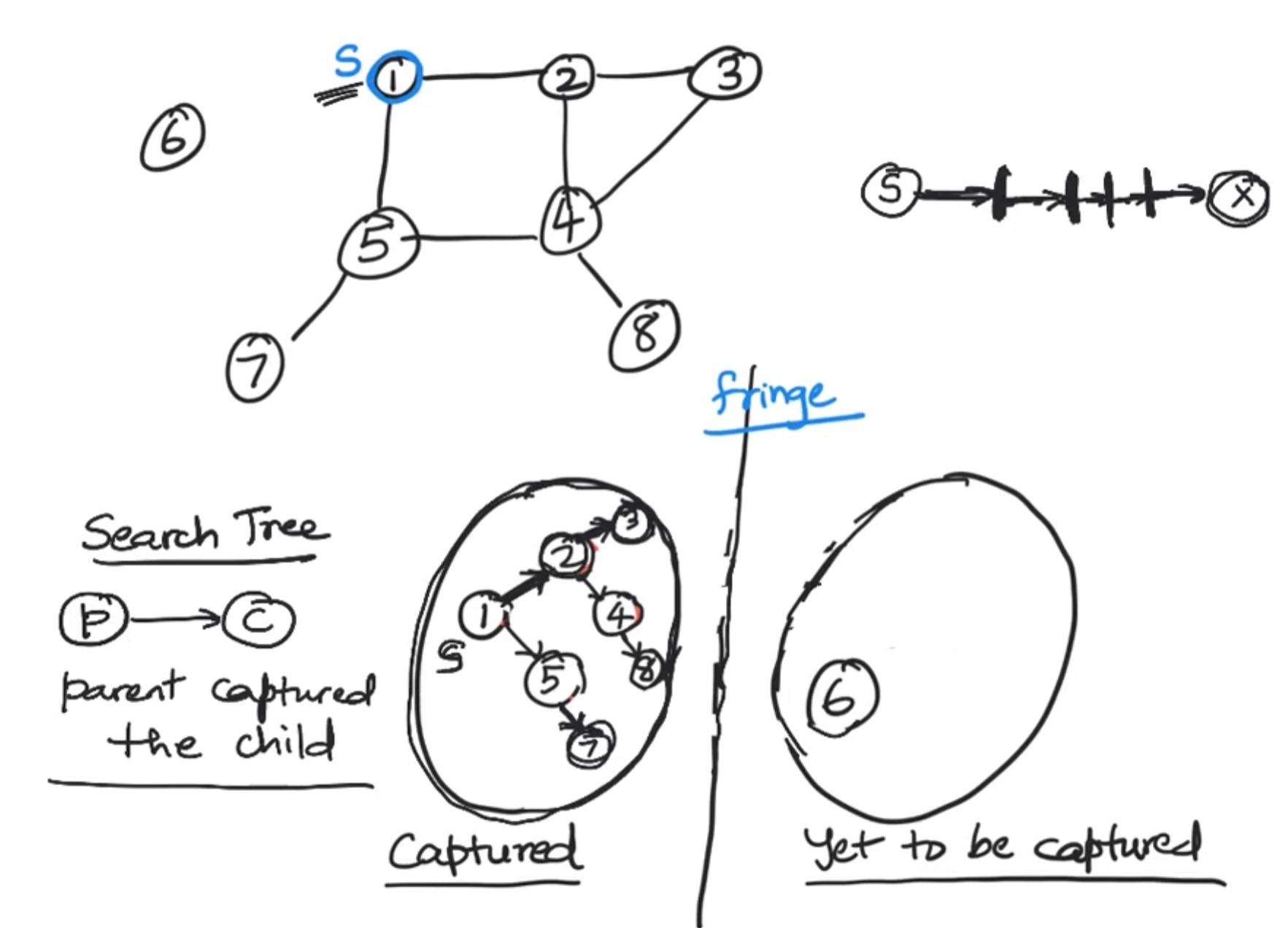
Start with a source vertex (starting vertex). Assume it is in captured set. Rest of the vertices are in yet to be captured set. From the source vertex, edges could be connected to some vertices. These are called fringe edges. Randomly pick one of the fringe edge and add it to the captured set and also mark it as child of the vertex that was used ..in this case source vertex as parent. Now the new vertex that is captured may have fringe edges in yet to be captured set. Randomly pick one of them and add it to the captured set and mark the hierarchy as the new vertex as child of the earlier vertex.

At the end of this exercise,

• We get a serach tree with source vertex as the root
• The set of captured vertices = the set of reachable nodes from S. If this set is not equal to the set of all the vertices, then it is not a connected graph.

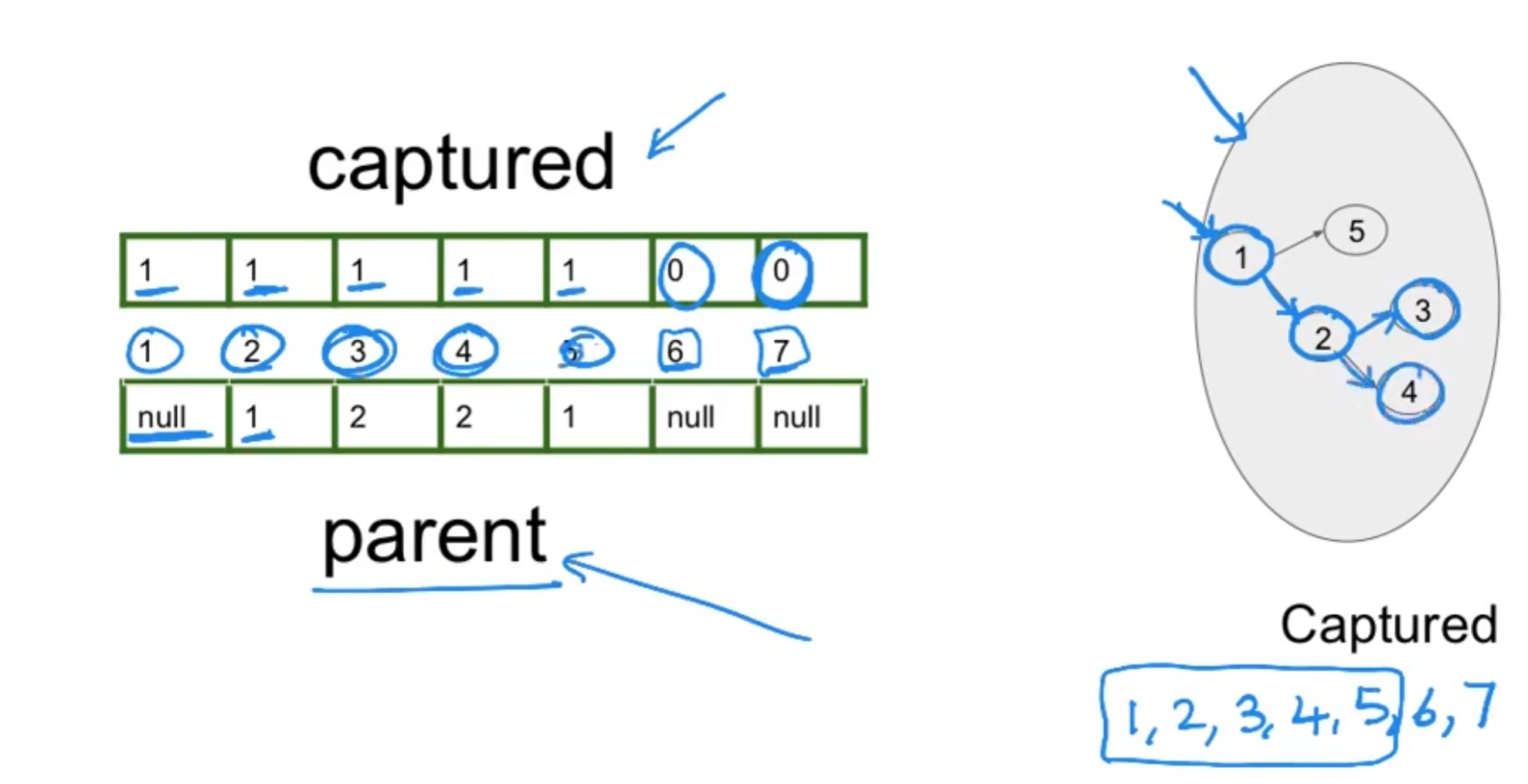
parent array for creating search tree. It is intialized to null. Pseudo code

def search (s):
    captured[s] = 1
    while there exists fringe edge:
       pick a random one ==> (u, v)
       captured[v] = 1
       parent[v] = u

• This same template is used by all the algorithms as well as directed

or undirected graphs. The graph algorithms such as BFS, DFS, Djikstra, prince, A*, best first search all follow this template. They differ in the policy of how fringe edges are selected to extract next vertex.

Graph Algorithms Template

• Different algorithms are going to lead to different serach trees and different properties.

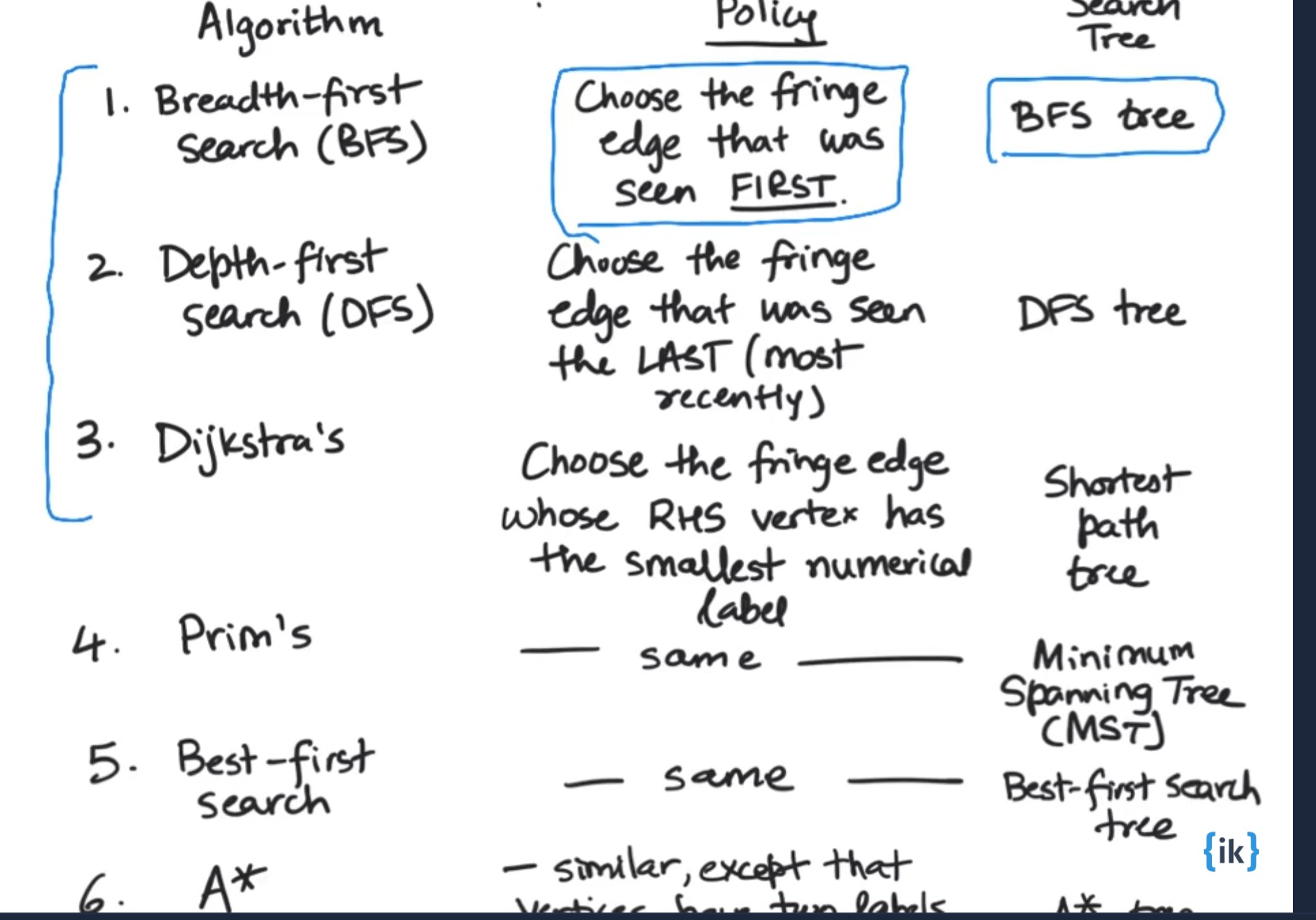
• Djikstra, best_search, A* algorithms use additional book keeping to know smallest numerical labels for vertices. i.e for each of the vertices in the yet to be captured set, each of the vertex also has an associated numerical label and depending on how this numerical label is matched results in shortest path tree or minimum spanning tree etc.

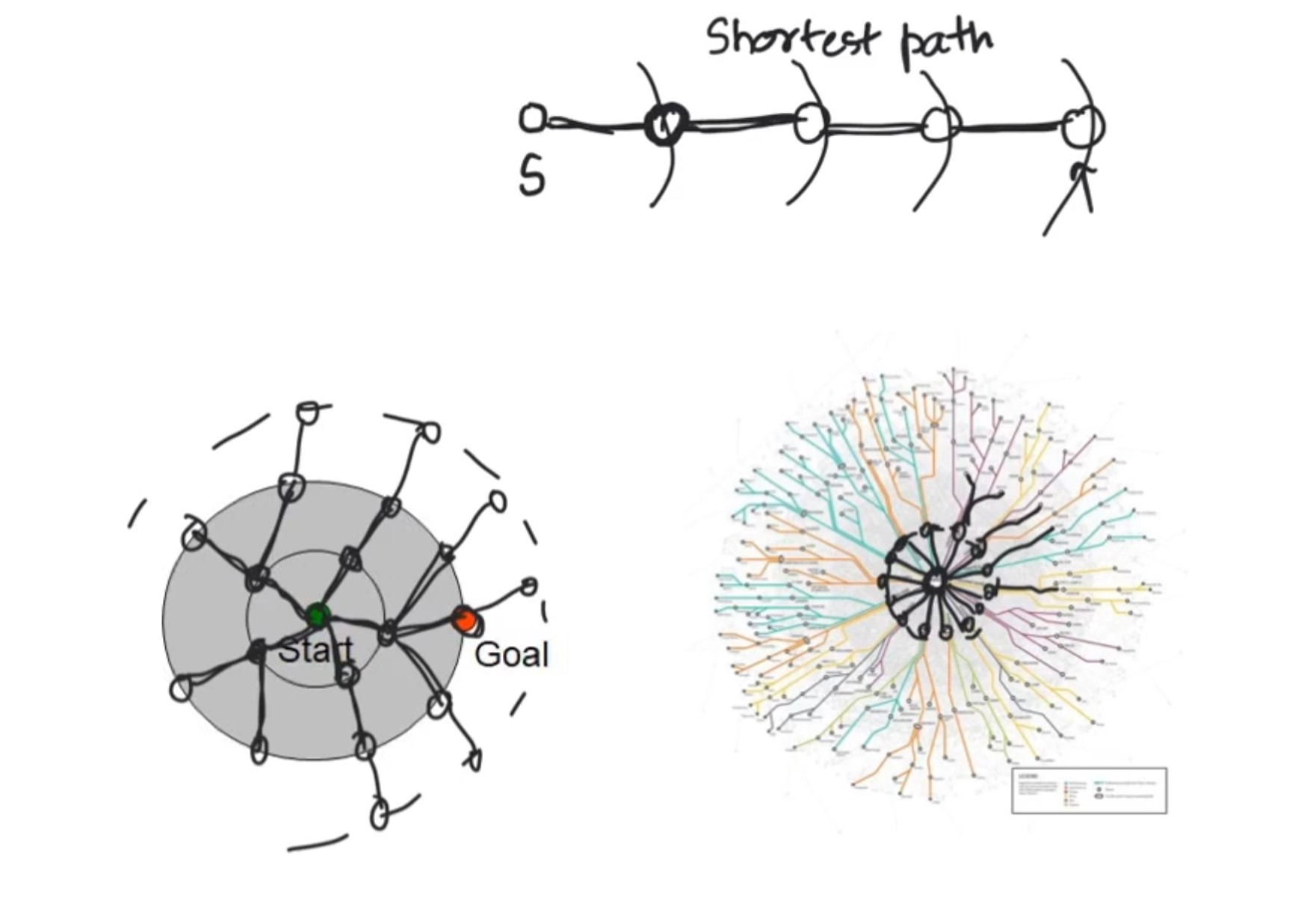
BFS Requirements

• Explores graph from increasing order of distance from the source S.

• First neighbors one hop away from S are brought into captured set. Then it does 2 hop, 3 hop and so on until all reachable vertices are captured.

• Start from a random start node in the captured set and find all its fringe edge neighbors as 1 hop. Then from these 1 hop neighbors, identify the new fringe edges that go to 2hop neighbors of S and keep expanding out until all the vertices are captured.

• If we have a particular destination/vertex in the graph, then stop the search when the desired vertex is identified.

• An analogy of BFS is how a disease spreads across community.

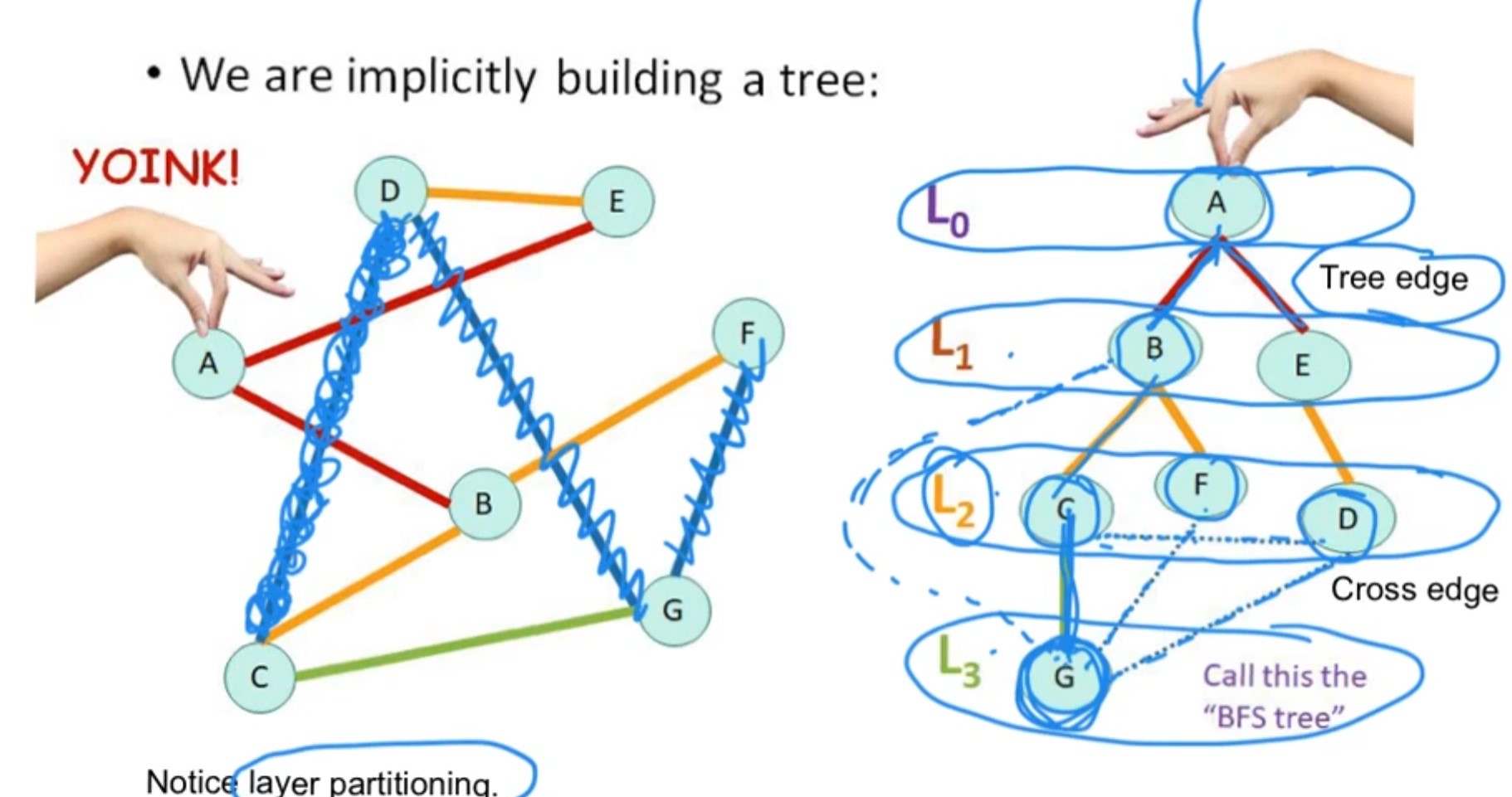
Special Case: How to handle cycles in BFS: -Whenever a vertex is discovered, even before adding to captured set, we need to check if it is present in the visited set, it should not be processed again to avoid cycles.

Cross edges denote cycles in BFS tree. It can be in same layer or adjaccent layer.

Algorithm: Depth First Search:

• Instead of going broad, go in depth and backtrack as necessary
• Replace queue with stack and this si the only change.
• The time complexity remains the same O(m+n) for both BFS and DFS.
  • The time taken to process one vertex is degree of the vertex
  • Time taken for all the vertices is same as twice the number of edges = O(m).
  • since there is O(n) time for initialization, total time is O(m+n) In recursive implementation of DFS, visited and captured are more or less same. Time complexity of recursive implementation is same as that of stack implementation. Space complexity

Finding Connected components of a graph using DFS:

This can be done with BFS too. findcomponenet() does not change.

In the visited array list, we can see which all vertices ahve the same compoenent value and counting the vertics of same compoennt value tells us that atleast there is #ofvertices - 1 edges present for that compoenent value. IF ther eare multiple such edge counts, then clealyr compoenents are not connected and tehre does not exist eulerian cylce or path.

General Problem Strategy:

• Step 1: Build the graph
  • Gather the vertices and their ids. In most cases, the ids are convenient 0 to n-1 integers and these can be used as array index.
  • One dimensional array of empty list is used for adjacency list.
  • n is the number of vertices.
  • The given edge list is transformed into adjacency list.
• Step 2: Write function for BFS or DFS
• Step 3: Outer loop which runs as many BFS or DFS functions as required to explore the graph

References:

Omkar’s Graph slides

{{ relref . “Python Exercises” }}