Linked List Problems
- Problems
- 1. Middle of the linked list - LC 876 - Easy
- 2. Linked List Cycle - LC 141 - Easy
- 3. Happy Number - LC202 - Easy
- 4. Linked List Cycle II - LC142 - Easy
- 5. Circular Array Loop - LC 457 - Medium
- 6. Pseudo-Random Number - UVA Competitive problem
- 7. Find the duplicate number - LC 287 - Medium
- 8. Design Linked List - LC 707 - Medium
- 9. Delete Node in a Linked List - LC 237 - Medium
- 10. Remove Linked List Elements - LC 203 - Easy
- 11. Remove Nth Node From End of List - LC 19 - Medium
- 12. Swapping Nodes in a linked list - LC 1721 - Medium
- 13. Remove Duplicates from Sorted List - LC 83 - Easy
- 14. Remove Duplicates from sorted list-II - LC 82 - Medium
- 15. Delete N Nodes after M Nodes of a linked list - LC 1474 - Easy
- 16. Insert Into a sorted circular linked list - Medium - 708
- 17. Merge two sorted lists - Easy - 21
- 18. Sort List - Medium - 148
- 19. Merge k sorted lists - Hard - 23
- 20. Insertion sort list - Medium - 147
- 21. Partition List - Medium - 86
- 22. Rotate List - Medium - 61
- 23. Reverse Linked List - LC 206 - Easy
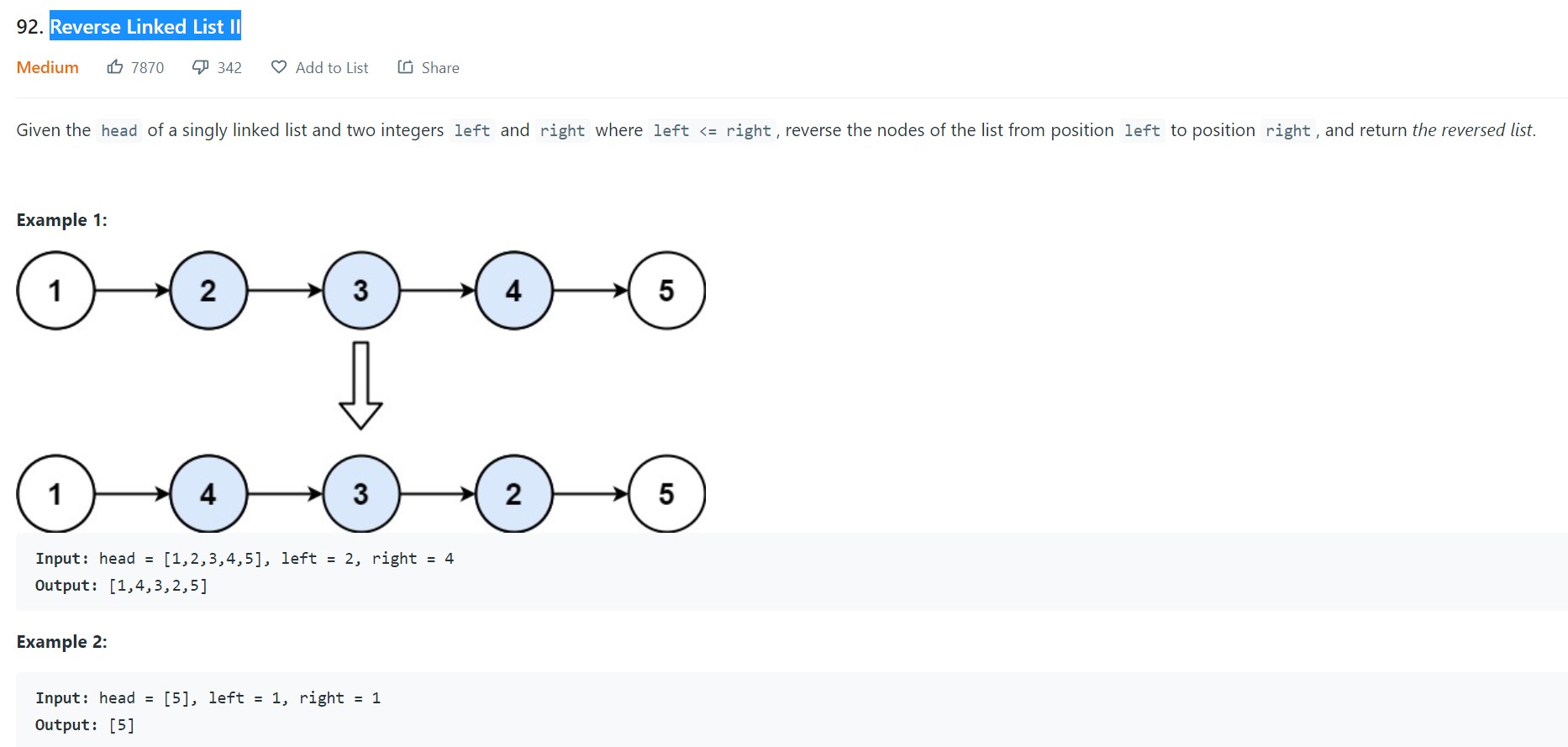
- 24. Reverse Linked List II - LC 92 - Medium
- 25. Palindrome Linked List - LC 234 - Easy
- 26. Reorder List - Medium - 143
- 27. Reverse Nodes in k-group - Hard - 25
- References:
Problems
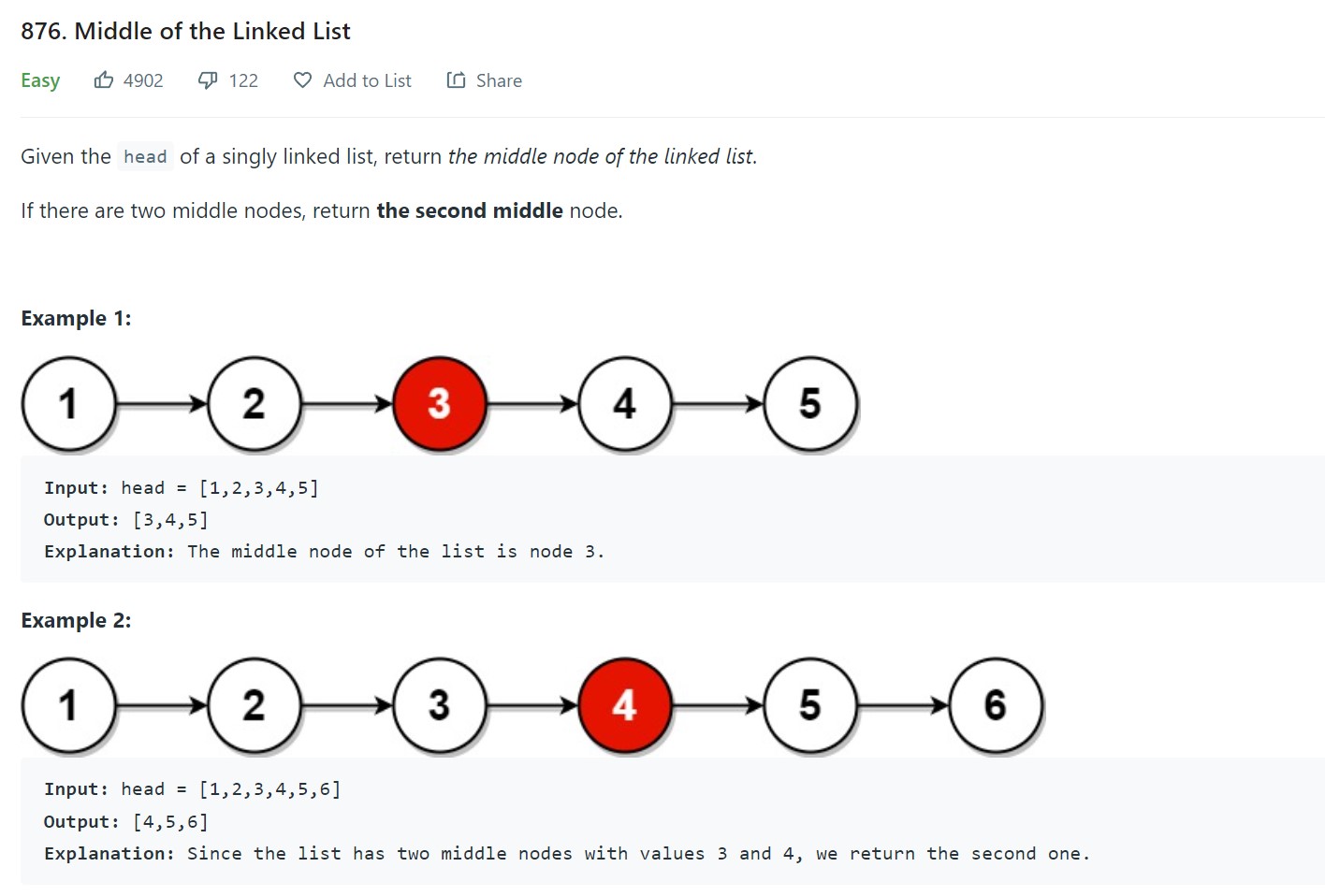
1. Middle of the linked list - LC 876 - Easy
Problem Statement - LC876
Video - LC876
Approaches and Thought process - LC876
-
Naive approach would be first to traverse the entire list to find the length fo the list. This is followed by another traversal from the head to the half of the length.
-
Space time tradeoff: Use a little extra space to cut down the number of iterations (time)
-
Slow and Fast Pointer use cases:
- Finding penultimate element of a linked list. Fast pointer goes two steps and slow poitner stays one step behind. This can be now generalized (say we need to find 5th element from end) we can space the fast and slow pointers to be of distance 5.
-
The question explicitly states there is atleast one Node. So we do not make an explicit check to see if head is None. This may not be the case with other problems.
-
We should let the while loop complete and at the end of the while loop, we expect fast pointer to be on the last node and the slow pointer in the middle.
-
Since the question requires to return the second middle element, this happens only when we have even number of nodes in the list. In this case fast pointer will be on the penultimate node. So we have to check if the fastptr.next is Null and if so, advance the slow pointer one step to pick the second middle element. This is conditional.
-
The problem asks us to return the reference to the middle node and not its value. This means the output will have all the values of the nodes starting from the middle node and not just the middle node.
Code - LC876
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def middleNode(self, head: Optional[ListNode]) -> Optional[ListNode]:
fastptr = head
slowptr = head
while fastptr.next is not None and fastptr.next.next is not None:
slowptr = slowptr.next
fastptr = fastptr.next.next
if fastptr.next is not None:
slowptr = slowptr.next
return slowptr
Complexity Analysis - LC876
- Time Complexity: We have to do one full traversal before we can do any validation. So the complexity is \(\color{green}{O(N)}\)
- Space Complexity: \(\color{green}{O(1)}\)
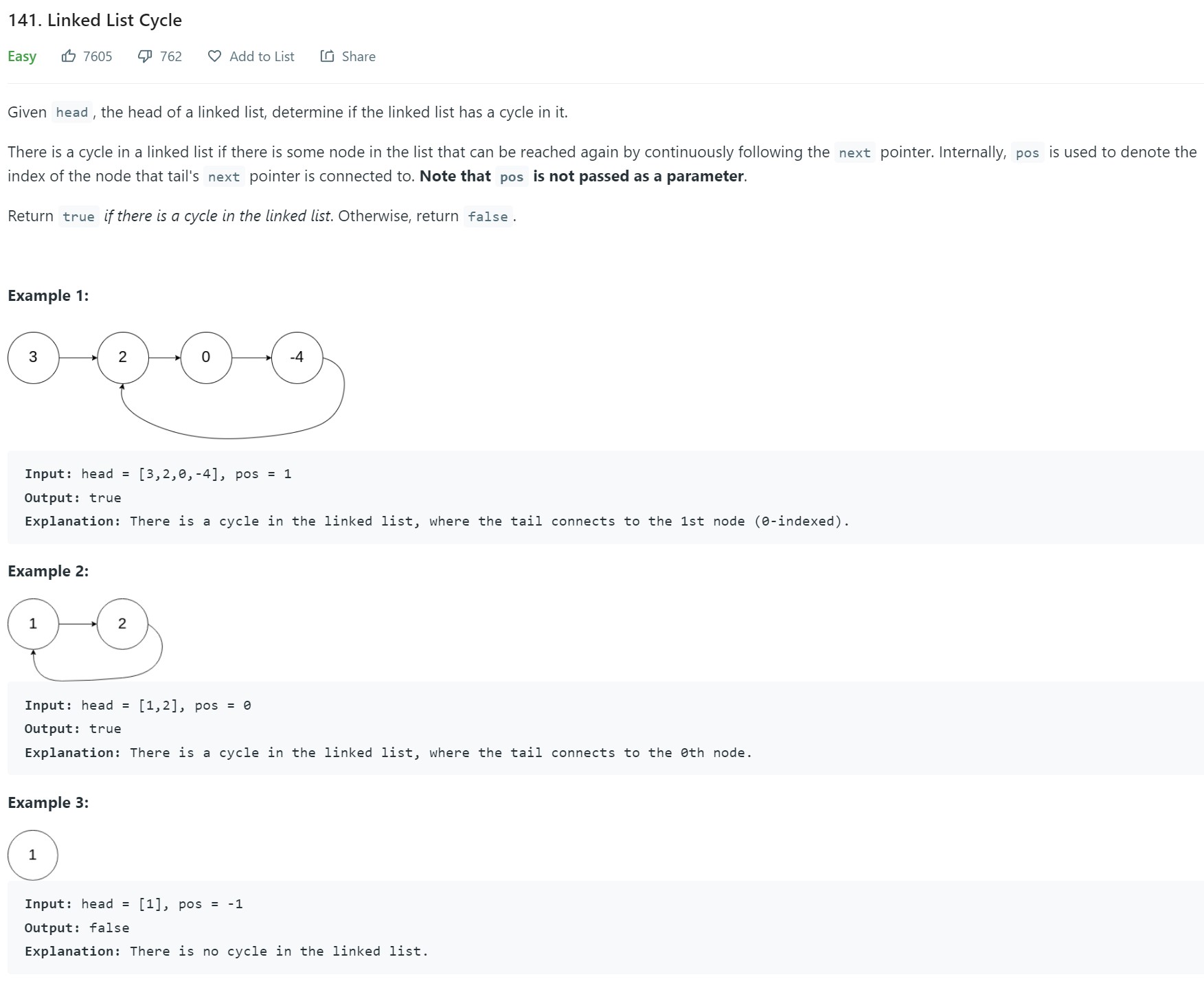
2. Linked List Cycle - LC 141 - Easy
Problem Statement - LC141
Video - LC141
Approach(es) and Thought Process - LC141
- Unlike the problem where we find the middle of the node, here there is a potential cycle. So we cannot let the while loop run completely because it can get into infinite loop. The check for fastptr == slowptr should happen inside the while loop. Rest of the logic remains the same.
-
Edge Case(s):
- In this problem, it is not specified that there is atleast one Node. This means we need an explicit check to confirm if head is None or not.
Code - LC141
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
fastptr = head
slowptr = head
if head is None:
return False
while fastptr.next is not None and fastptr.next.next is not None:
slowptr = slowptr.next
fastptr = fastptr.next.next
if slowptr == fastptr:
return True
return False
Complexity Analysis - LC141
- Time Complexity: The fastptr will do one full traversal and continue to loop back before meeting the slow pointer. This means the complexity is \(\color{green}{O(n + \lambda)} \approx \color{green}{O(N)}\)
- Space Complexity: \(\color{green}{O(1)}\)
3. Happy Number - LC202 - Easy
Problem Statement - LC202
Video - LC202
Approaches and Thought Process - LC202
class Solution:
def isHappy(self, n: int) -> bool:
def sum_of_squares(x):
total = 0
while x != 0:
total += ((x % 10) ** 2)
x = x // 10
return total
seen = set()
while n !=1 and n not in seen:
seen.add(n)
n = sum_of_squares(n)
return (n == 1)
Code - LC202
class Solution:
def isHappy(self, n: int) -> bool:
def sum_of_squares(x):
total = 0
while x != 0:
total += ((x % 10) ** 2)
x = x // 10
return total
hare = tortoise = n
while True:
hare = sum_of_squares(hare)
hare = sum_of_squares(hare)
tortoise = sum_of_squares(tortoise)
if hare == tortoise:
return (hare == 1)
Complexity Analysis - LC202
4. Linked List Cycle II - LC142 - Easy
Problem Statement - LC142
Video - LC142
Approaches and Thought Process - LC142
Code - LC142
Complexity Analysis - LC142
5. Circular Array Loop - LC 457 - Medium
Problem Statement - LC457
Video - LC457
Approaches and Thought Process - LC457
Code - LC457
Complexity Analysis - LC457
6. Pseudo-Random Number - UVA Competitive problem
Problem Statement - UVA350
Video - UVA350
Approaches and Thought Process - UVA350
Code - UVA350
Complexity Analysis - UVA350
7. Find the duplicate number - LC 287 - Medium
Problem Statement - LC287
Video - LC287
Approaches and Thought Process - LC287
Code - LC287
Complexity Analysis - LC287
8. Design Linked List - LC 707 - Medium
Problem Statement - LC707
Video - LC707
Approaches and Thought Process - LC707
Code - LC707
Complexity Analysis - LC 707
9. Delete Node in a Linked List - LC 237 - Medium
Problem Statement - LC237
Video - LC237
Approaches and Thought Process - LC237
Code - LC237
Complexity Analysis - LC237
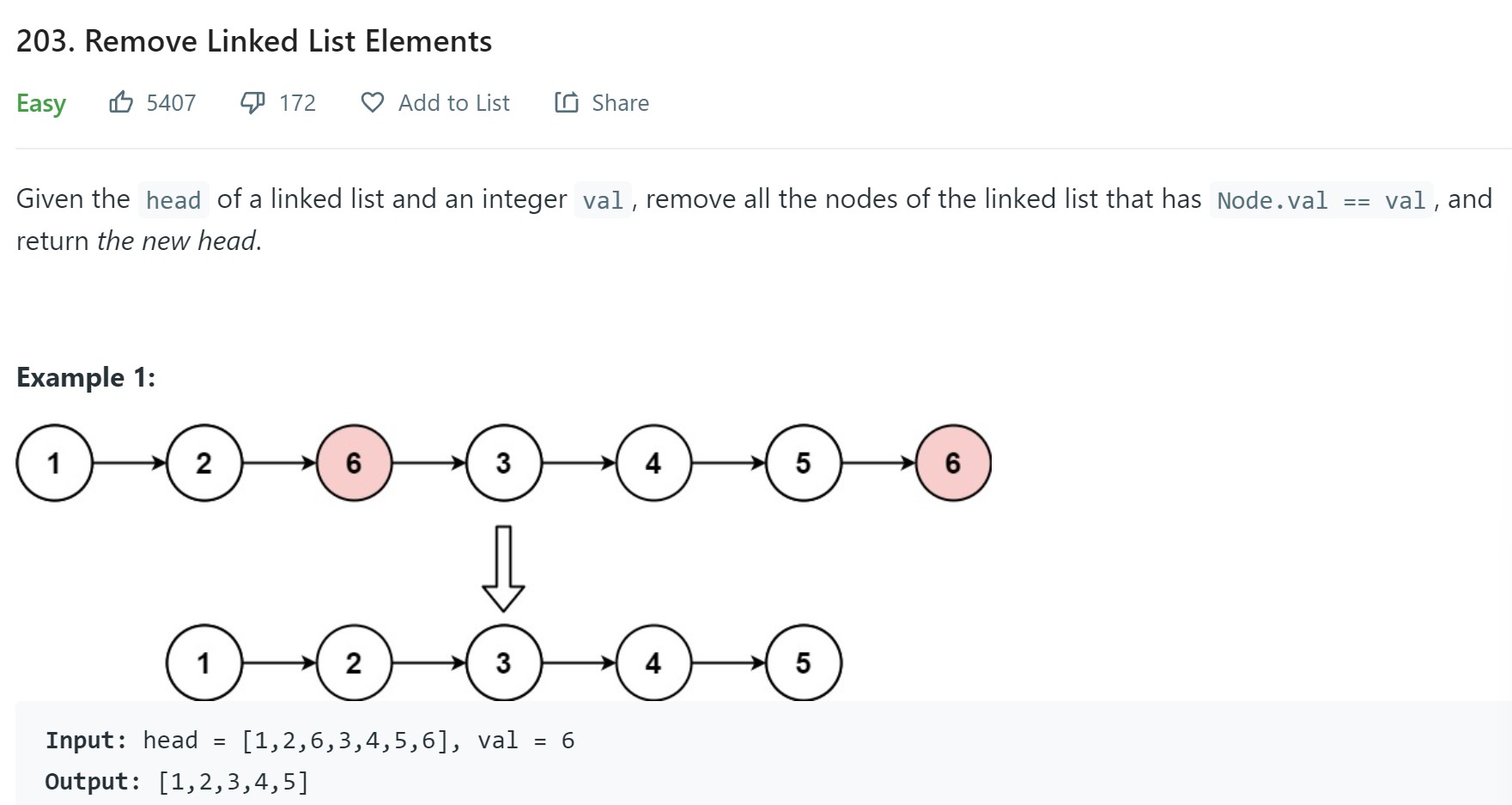
10. Remove Linked List Elements - LC 203 - Easy
Problem Statement - 203
Video - 203
Approaches and Thought Process - 203
Code - 203
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:
sentinel = ListNode(float("-inf"), head)
prev = sentinel
cur = head
while cur:
if cur.val == val:
prev.next = cur.next
cur = cur.next
else:
prev = cur
cur = cur.next
head = sentinel.next
return head
Complexity Analysis - 203
- Time Complexity: \(\color{green}{O(N)}\)
- Space Complexity: \(\color{green}{O(1)}\)
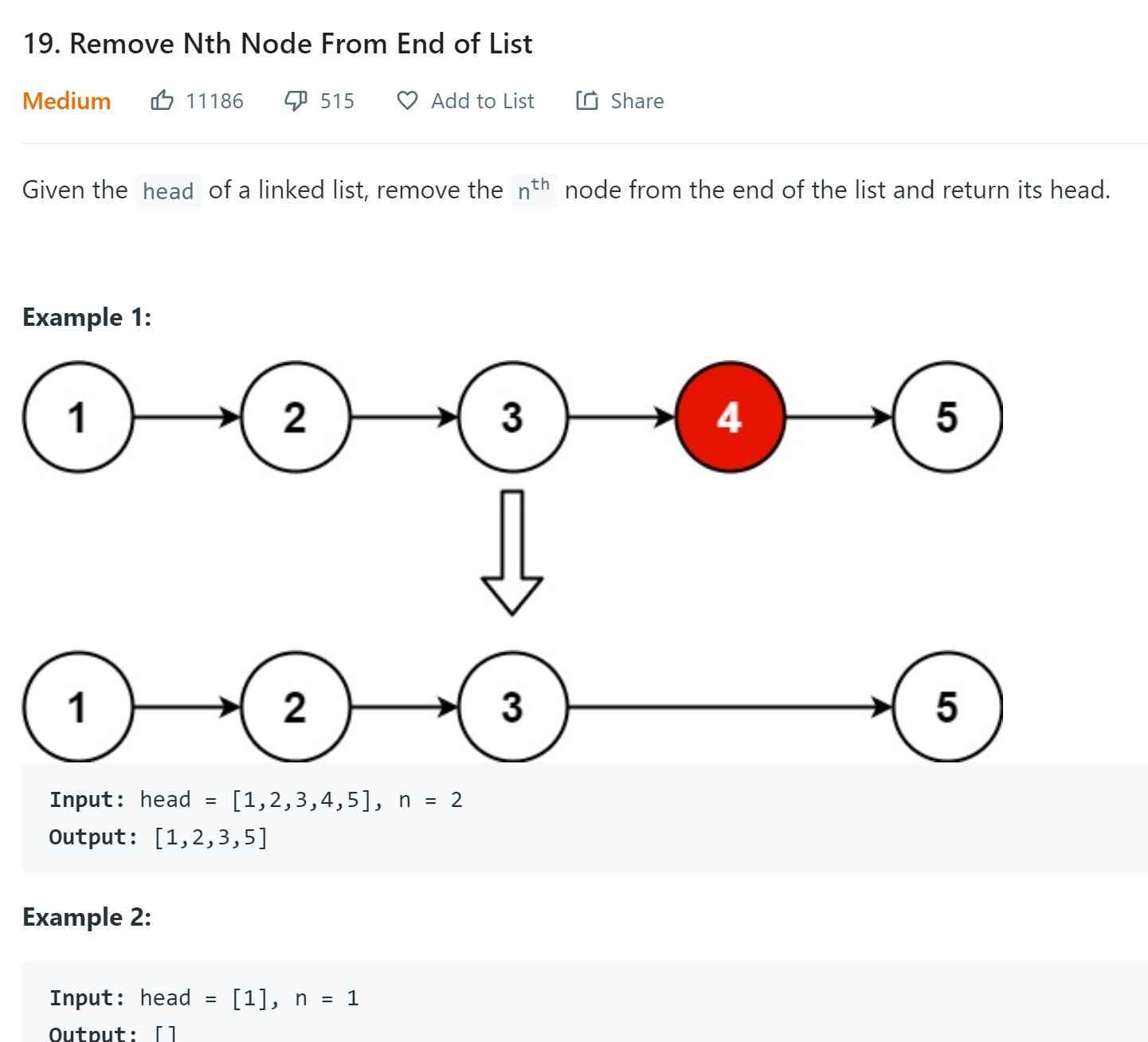
11. Remove Nth Node From End of List - LC 19 - Medium
Problem Statement - LC19
Video - LC19
Approaches and Thought Process - LC19
Code - LC19
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
sentinel = ListNode(float("-inf"), head)
leader = sentinel
for _ in range(n):
leader = leader.next
follower = sentinel
while leader:
leader = leader.next
pred = follower
follower = follower.next
pred.next = follower.next
head = sentinel.next
return head
Complexity Analysis - LC19
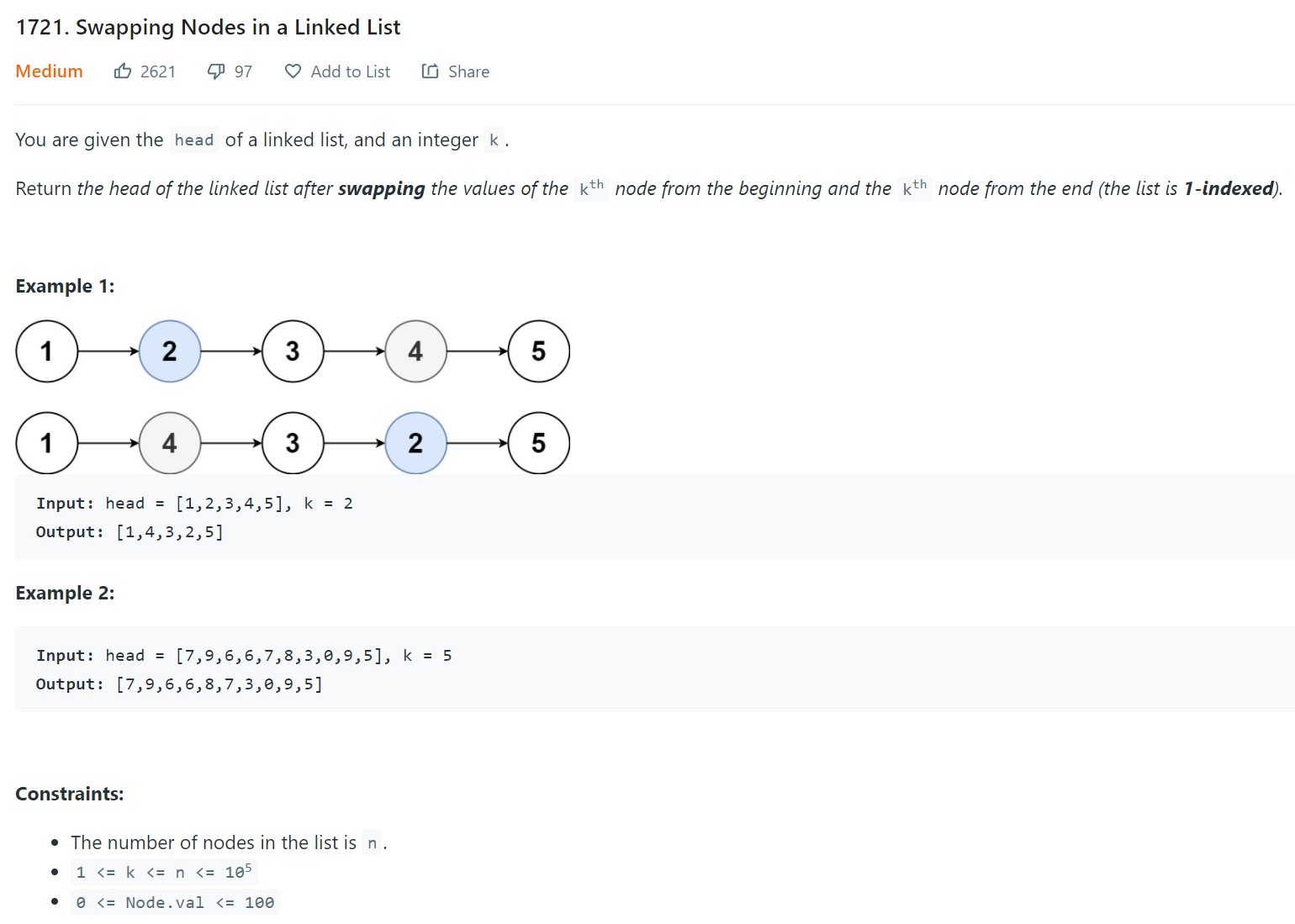
12. Swapping Nodes in a linked list - LC 1721 - Medium
Problem Statement - LC1721
Video - LC1721
No Video. This was not covered by Omkar. Though it is related to the above problem
Approaches and Thought Process - LC1721
- Brute Force Approach: Do one pass to calculate the length of the list Do second pass to find kth node from the front. Do third pass to find kth node from the last (n - k) from the front. Swap the nodes.
- Single Pass approach: Use the slow and fast pointer approach. Slow pointer starts when fast pointer reaches k nodes from the head.
Code - 1721
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def swapNodes(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:
length = 0
front = end = None
cur = head
while cur:
length += 1
if end is not None:
end = end.next
if length == k:
front = cur
end = head
cur = cur.next
front.val, end.val = end.val, front.val
return head
Complexity Analysis - LC1721
Iterative Approach
- Time Complexity: \(O(n)\)
- Space Complexity: \(O(1)\)
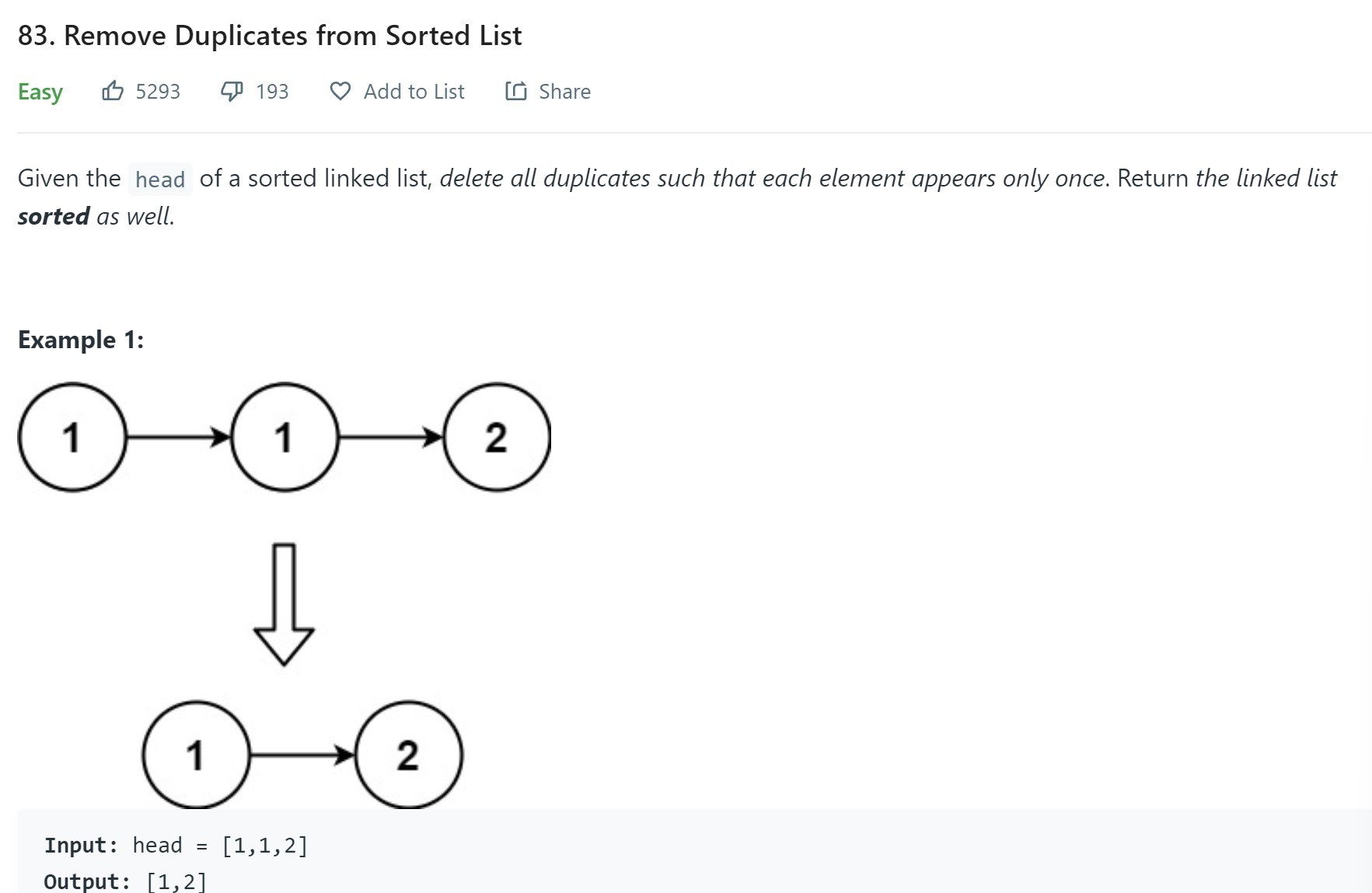
13. Remove Duplicates from Sorted List - LC 83 - Easy
Problem Statement - LC83
Video - LC83
Approaches and Thought Process - LC83
- We know the list is sorted. We do not know if it is empty or not.
- There could be more than one duplicates for a given value.
- Removing duplicates is same as deleting a node..Instead of deleting a node of a particular value, we delete if the value matches the previous node.
- Since we may have many instances of duplicate values, we compare it using if….else instead of adding this condition with while loop itself.
- What is the work to be done on current node?
- How do we know the current node is duplicate? Since the list is sorted, the value should match previous node or the next value.
- We could check for the next value or check for the previous value and if it matches, delete the node.
- We use sentinel/dummy node to start with and predecessor points to it and current starts from head.
- Hence initialize the sentinel node to -infinity so that it is very unlikely to be same as that of the current node at the beginning.
Code - LC83
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:
sentinel = ListNode(float("-inf"), head)
pred = sentinel
cur = head
while cur:
if cur.val == pred.val:
pred.next = cur.next
cur = cur.next
else:
pred = cur
cur = cur.next
head = sentinel.next
return head
Complexity Analysis - LC 83
- Time Complexity: \(\color{green}{O(N)}\)
- Space Complexity: \(\color{green}{O(1)}\)
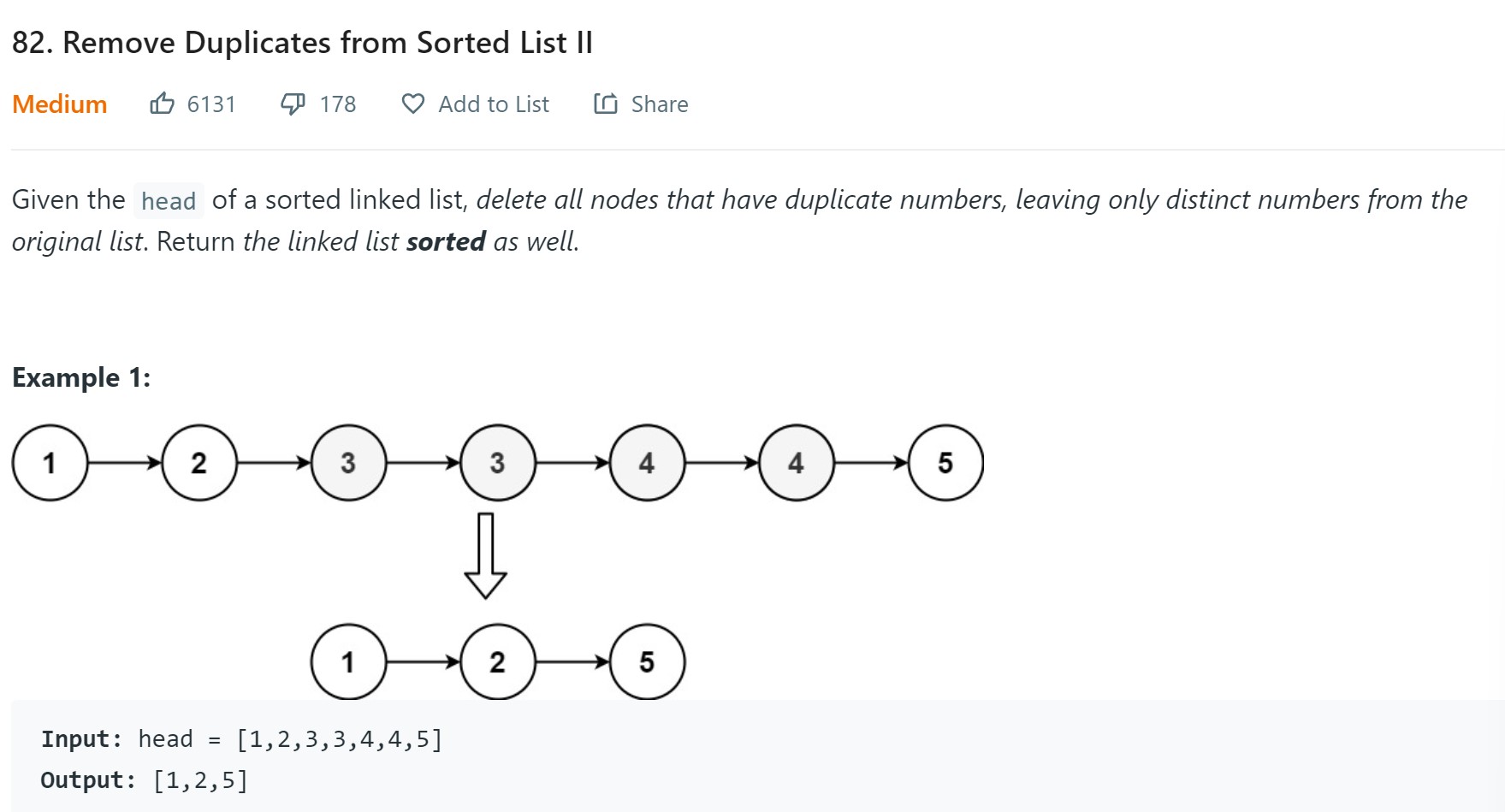
14. Remove Duplicates from sorted list-II - LC 82 - Medium
Problem Statement - LC82
Video - LC82
Approaches and Thought Process - LC82
Code - LC82
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:
sentinel = ListNode(float("-inf"), head)
pred = sentinel
cur = head
while cur:
if cur.next and cur.next.val == cur.val:
p = cur.next
while p and p.val == cur.val:
p = p.next
pred.next = p
cur = p
else:
pred = cur
cur = cur.next
head = sentinel.next
return head
Complexity Analysis - LC82
15. Delete N Nodes after M Nodes of a linked list - LC 1474 - Easy
Problem Statement - LC1474
Video - LC1474
Approaches and Thought Process - LC1474
- The repeating pattern is m nodes are preserved and n are deleted. So
each manager can handle the pattern and pass the next pattern to
subsequent manager.
Code - LC1474
class Solution:
def deleteNodes(self, head: ListNode, m: int, n: int) -> ListNode:
cur = head
pred = head
while cur:
#Move m nodes forward including the current one:
index = 1
while cur and index <= m:
pred = cur
cur = cur.next
index += 1
if cur is None:
break
# Bypass the next n nodes:
index = 1
p = cur
while p and index <= n:
p = p.next
index += 1
pred.next = p
cur = p
return head
Complexity Analysis - LC1474
16. Insert Into a sorted circular linked list - Medium - 708
Problem Statement - LC708
Video - LC708
Approaches and Thought Process - LC708
Instead of linked list, assume this is an array. As a lazy manager, assume the array is already sorted except for the last element.( n - 1). The job is to scan each element from n-2 backwards to find the right spot for n-1. While doing this, right shift the element. Then insert the element at the right place.
This same approach can be done for linked list too. However, since there is no easy way to scan from the right to left, we have to do this from left to right in the case of linked list. Imagine we are creating a new list as we pluck the element and insert in the right order. This means use a sentinel list. Once the node is extracted, we go through the sorted list (sentinel list) and find the node that has element greater than the current one and this is where we need to insert. To scan the sorted list, use pred and cur node. Tip: Think of creating a new list instead of manipulating the existing list helps with linked list problems and keeps the code simpler.
Code - LC708
class Solution:
def insert(self, head: 'Node', insertVal: int) -> 'Node':
if not head:
head = Node(insertVal)
head.next = head
return head
curr = head
while True:
if curr.val <= insertVal <= curr.next.val:
break
# last element
if curr.val>curr.next.val:
if curr.val <= insertVal >= curr.next.val:
break
elif curr.val >= insertVal <= curr.next.val:
break
curr = curr.next
# all elements are equal
if curr == head:
break
new_node = Node(insertVal)
tmp = curr.next
curr.next = new_node
new_node.next = tmp
return head
Complexity Analysis - LC708
Time complexity: Time taken to pull node is constant. Finding the right spot is the time consuming part. To find the right spot takes O(i) for the ith node. sigma i=1 to n, O(i) = O(n^2)
Aux Space = O(1)
17. Merge two sorted lists - Easy - 21
Problem Statement - LC21
Video - LC21
Approaches and Thought Process - LC21
Code - LC21
Complexity Analysis - LC21
18. Sort List - Medium - 148
Problem Statement - LC148
Video - LC148
Approaches and Thought Process - LC148
Code - LC148
Complexity Analysis - LC148
19. Merge k sorted lists - Hard - 23
Problem Statement - LC23
Video - LC23
Approaches and Thought Process - LC23
Code - LC23
Complexity Analysis - LC23
20. Insertion sort list - Medium - 147
Problem Statement - LC147
Video - LC147
Approaches and Thought Process - LC147
Code - LC147
Complexity Analysis - LC147
21. Partition List - Medium - 86
Problem Statement - LC86
Video - LC86
Approaches and Thought Process - LC86
Code - LC86
Complexity Analysis - LC86
22. Rotate List - Medium - 61
Problem Statement - LC61
Video - LC61
Approaches and Thought Process - LC61
Code - LC61
Complexity Analysis - LC61
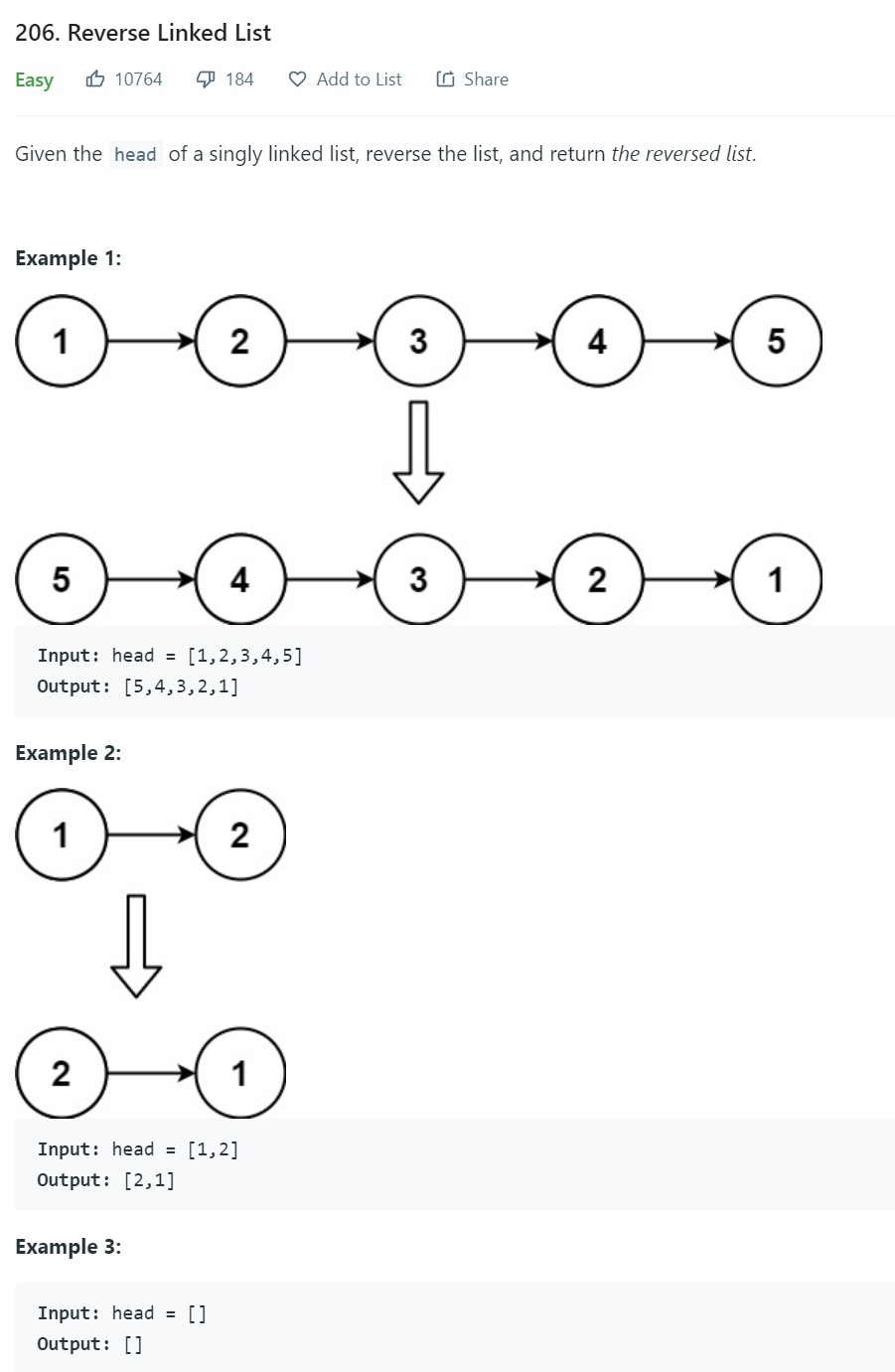
23. Reverse Linked List - LC 206 - Easy
Problem Statement
Video
Approaches and Thought Process
- Building Blocks for handling Linked List Problems
-
Use Hare and tortoise pattern:- Use two pointers of different speed (slow and fast) along the list
-
Using Sentinels:- This helps to avoid edge cases. Wherever there is a chance of insertion or deletion can change the head node of hte linked list, always good to use dummy node towards left of the head, point to head to avoid dealing with empty list edge case. At any stage, head node will be given by sentinel.next.
When creating a new list (merging two or more sorted lists or rearranging the list in a way output is created as fresh list), sentinel node helps.
-
Mental representation for insertions and deletions:- A specific way of writing the code so that whenever insertion or deletion of node from or into linked list, we will use curr pointer that will land up at node before the node to be inserted or deleted. In either case, we need predecessor pointer which can bypass curr pointer in the case of deletion and in the case of insertion, predecessor.next points to new node and new node’s next points to the current.
-
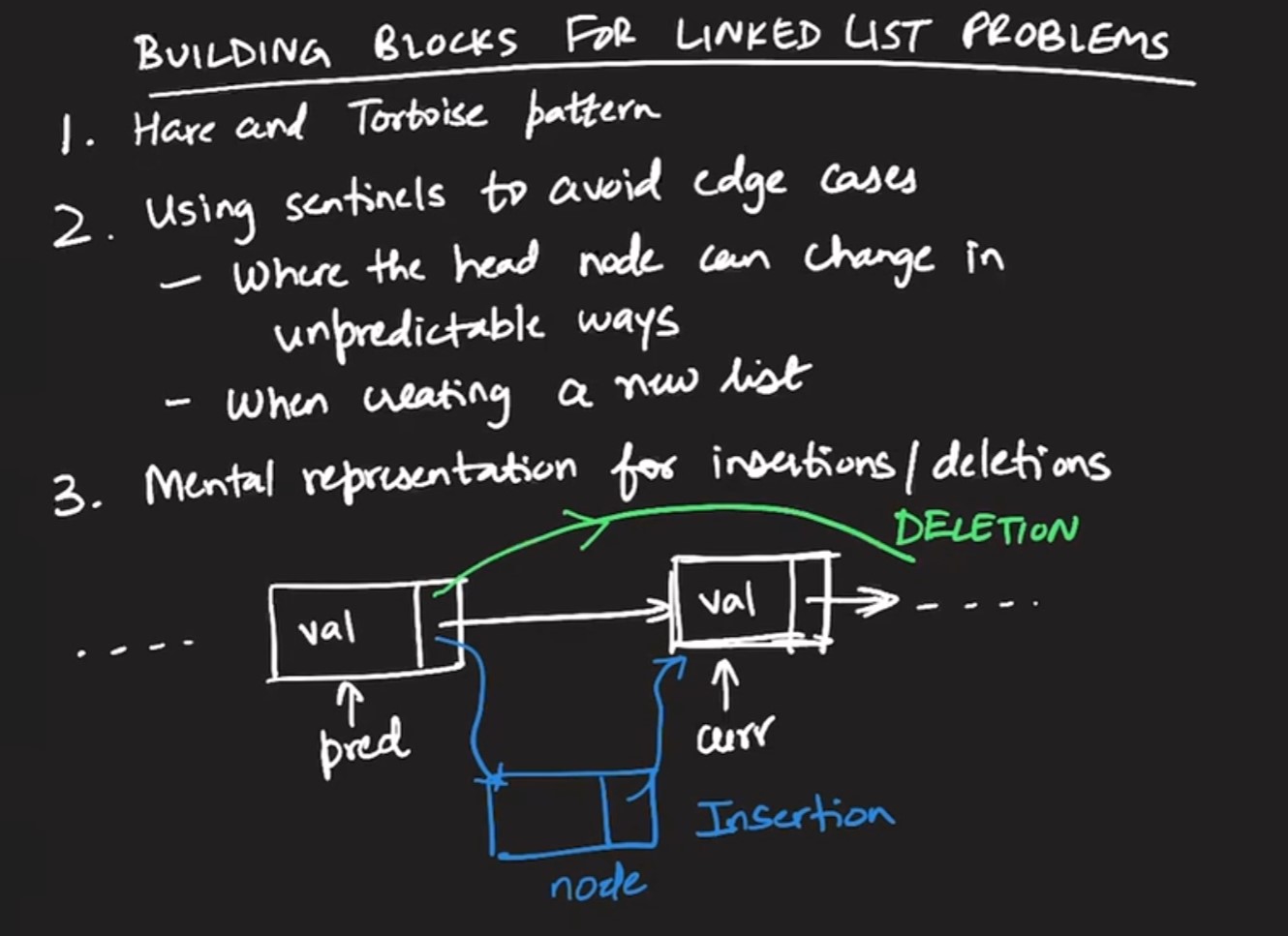
-
Could be explicitly asked to implement either recursively or iteratively or potentially both. Practice all of them. Preference is for iterative approach as for most linked list problems, the general expectation is time complexity of \(O(n)\) and space complexity of \(O(1)\). With recursive approach, stack space can be \(O(n)\)
-
Recursive implementation always result in decrease and conquer or divide and conquer. In Tree problems, recursive implementation is always preferred because we need to go in multiple directions.
-
Linked list has linear structure. To use decrease and conquer on linked list, do some work on the head node, and percolate some work to the single subordinate who does the same to node below until leaf node or last node is reached.
Bottom Up Recursive Approach: Bottom up approach on linked list is something like manager passing the remaining work to node below and the node below does the same to its node below and when the response percolate up, manager adds his/her own work and passes up.
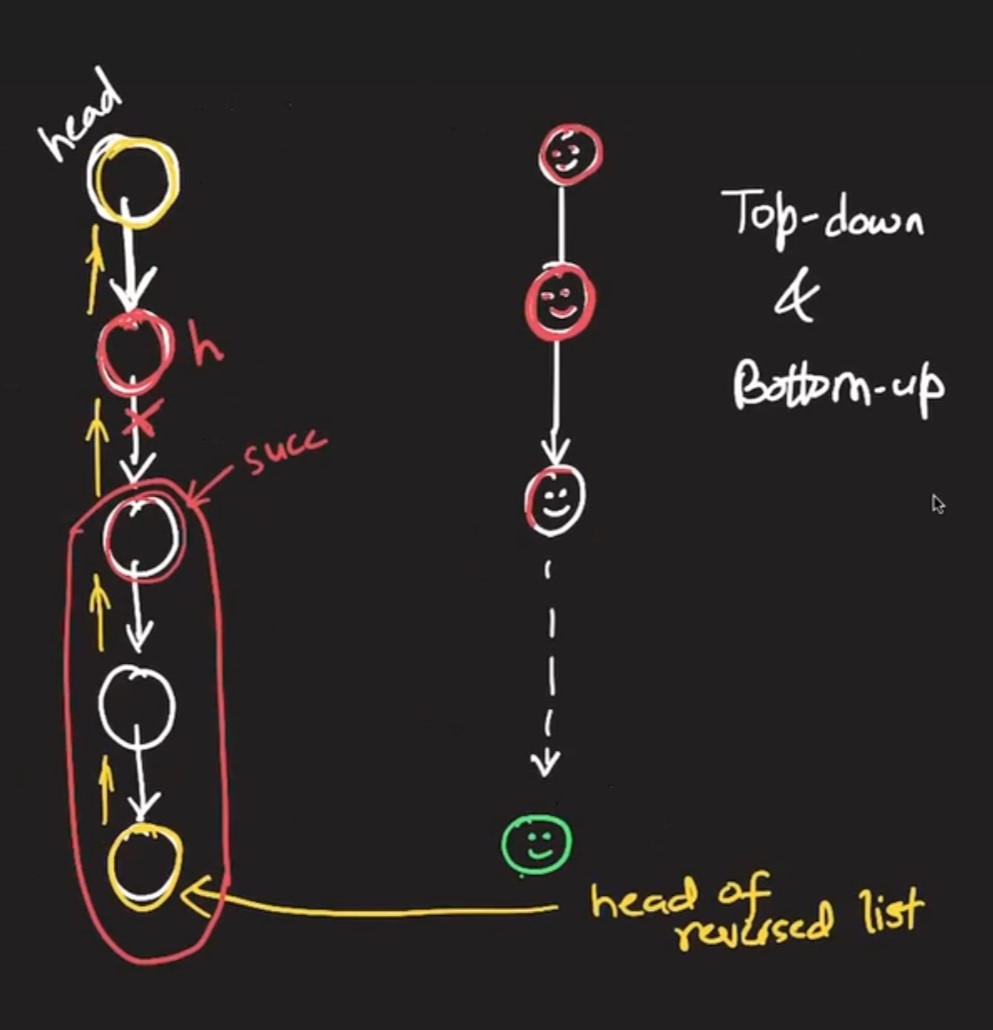
- In the bottom up dfs recursive code, the leaf level worker or last node sets the header of the linked list because we are reversing the list.
- An intermediate worker/node disconnects its successor/next after storing its successor in a variable and then appends to the tail.next (tail is return value from the recursive code)
Top Down Recursive Approach:
-
In the top down approach, each node/worker does some work and then hands over the rest to the subordinate.
-
Nothing comes back up. It is unidirectional. The link is changed as if in waterfall mode.
-
The assumption at any node is that everything above its node has been reversed and the manager has to take the current node and make it part of reversed list and pass the remaning list to subordinate.
-
The leaf node sets the global value to head pointer as no other node knows which node is the head.
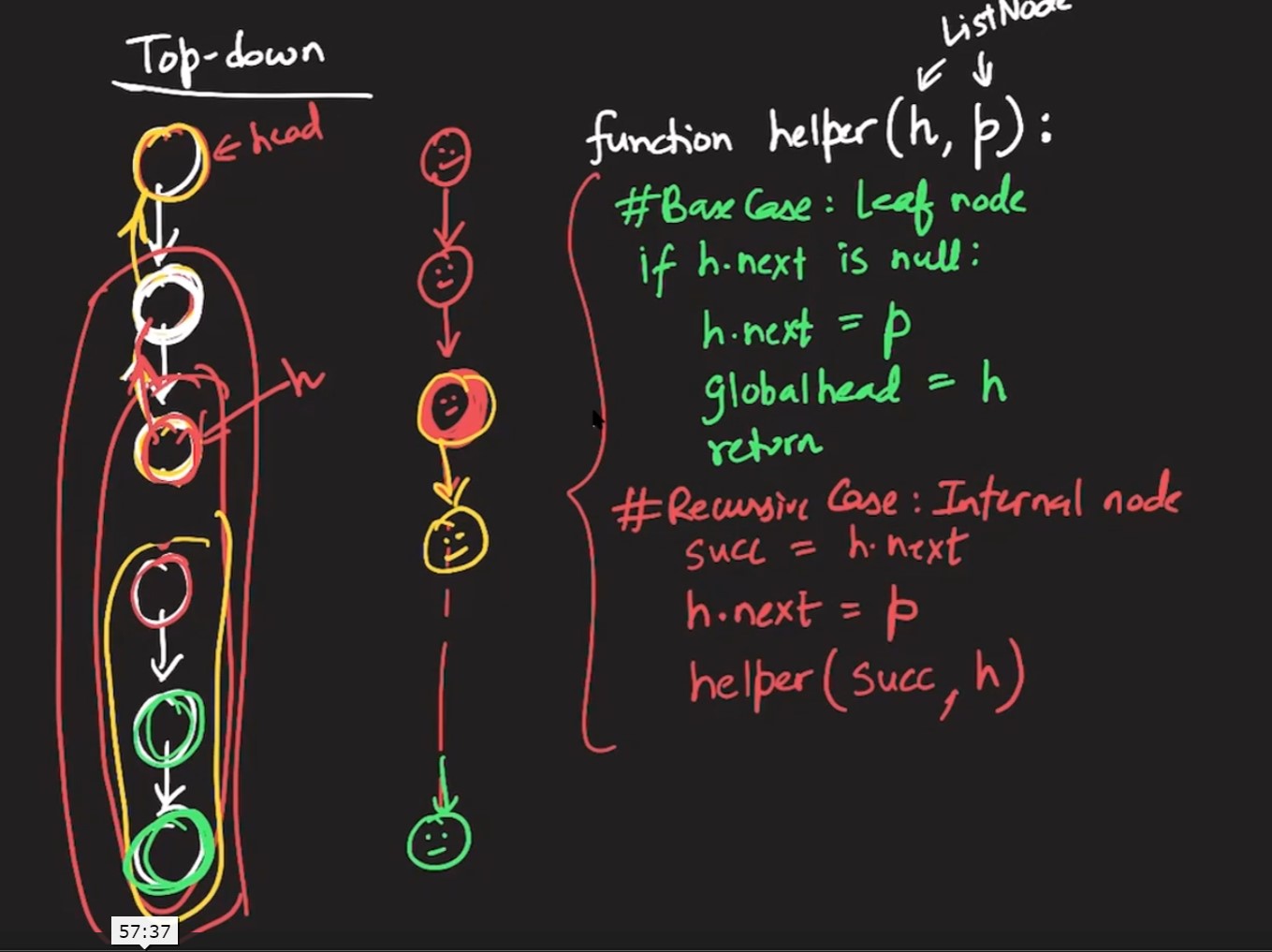
Iterative Approach:
- Every node has to update its cur.next to predecessor. Store the cur.next upfront and then update cur.next to predecessor.
- Predecessor starts with null and curr pointer starts with head. At the end of reversal, predecessor points to head as the last node becomes the head.
Code
Complexity Analysis
Bottom Up & Top Down DFS Recursive Code
- Time Complexity: \(\color{green}{O(n)}\)
- Space Complexity: Aux Space = \(\color{green}{O(1)}\) Implicit Stack Space = \(\color{green}{O(n)}\)
Iterative Approach
- Time Complexity: \(\color{green}{O(n)}\)
- Space Complexity: \(\color{green}{O(1)}\)
24. Reverse Linked List II - LC 92 - Medium
Problem Statement
Video
Approaches and Thought Process
- Use the same template as the previous
Reverse Linked Listproblem and adjust the length of curr pointer. - Curr pointer need not start from the head but from the left pointer and need not go until Null but until right pointer.
- At this point I know sublist would have reversed, take the tail node before curr node and add to the tail node of the curr node
- The head node may or may not remain the same. This edge case needs to be handled carefully. So sentinel node helps in this problem. In the previous problem, we knew the last node will be the head node.
Code
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseBetween(self, head: Optional[ListNode], left: int, right: int) -> Optional[ListNode]:
curr = head
index = 1
sentinel = ListNode(0, head)
prev = sentinel
# Step 1: Go to the index from head
while index != left:
prev = curr
curr = curr.next
index += 1
# Step 2: reverse the nodes between left and right index
save_curr = curr
save_prev = prev
prev = None
while index != right+1:
succ = curr.next
curr.next = prev
prev = curr
curr = succ
index += 1
# Step 3: Connect the rest of the pointers to both end of the reversed nodes
save_prev.next = prev
save_curr.next = curr
return sentinel.next
Complexity Analysis
Iterative Approach
- Time Complexity: \(O(n)\) Space Complexity: \(O(1)\)
25. Palindrome Linked List - LC 234 - Easy
Problem Statement
Video
Approaches and Thought Process
- The naive approach is to transform and conquer.
- Convert the linked list into array and using two pointer approach from both sides, we can validate if the elements are palindrome or not. However, this uses additional O(N) space complexity.
- To do this in space O(1) and time O(N):
- break the list into two equal parts using hare and tortoise approach
- reverse the second list
- Compaare elements in both the list and if they match, they are palindrome.
- It is possible that one of the list has one more element but still we do not care about this middle element. As long as all other elements match, it is a palindrome.
- Another thing to keep in mind is to leave things clean. By breaking and reversing the right side of the node, the entire list is mangled. We have to reverse the right half once again and connect it with the tail of the first list.
Code
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def isPalindrome(self, head: Optional[ListNode]) -> bool:
#Edge Case
if head is None and head.next is None:
return None
#Step 1: find the middle
slow = fast = head
while fast.next and fast.next.next:
slow = slow.next
fast = fast.next.next
cur = slow.next
slow.next = None
#Reverse the second part of the list
prev = None
while cur:
succ = cur.next
cur.next = prev
prev = cur
cur = succ
flag = True
#Compare first linked list with the second one
cur = prev
left = head
prev = None
while cur:
if left.val != cur.val:
flag = False
left = left.next
# Before moving the cur pointer, start reversing it once again to get back to the original state
succ = cur.next
cur.next = prev
prev = cur
cur = succ
head.next = prev
return flag
Complexity Analysis
Iterative Approach
- Time Complexity: \(O(n)\)
- Space Complexity: \(O(1)\)