Tree Problems
- Binary Tree Problems
- Breadth First Search
- 1. Binary Tree Level Order Traversal - LC 102 - Medium 👏👏👏👏👏👏👏👏👏👏👏
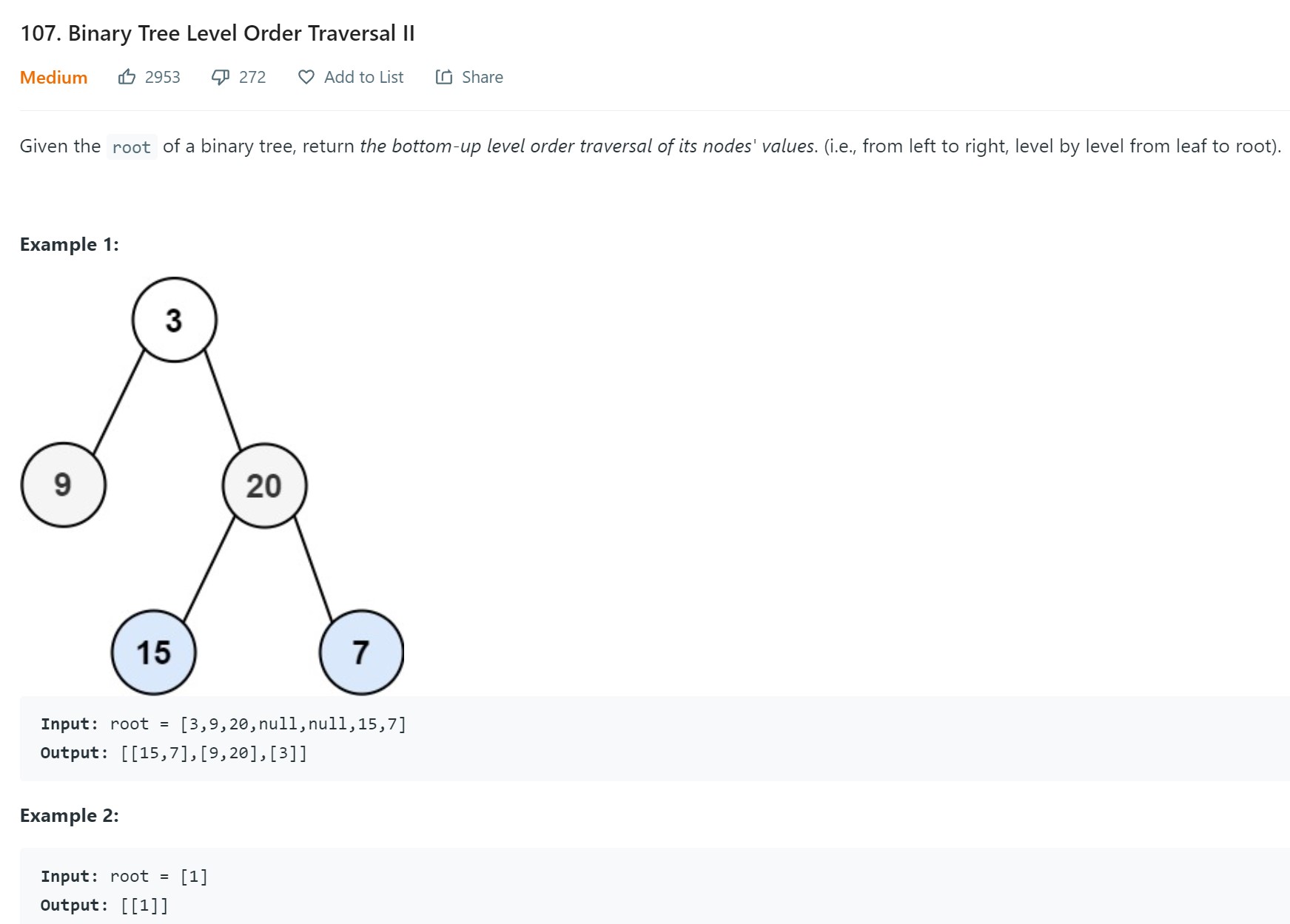
- 2. Binary Tree Level order traversal II - LC 107 - Medium🤞
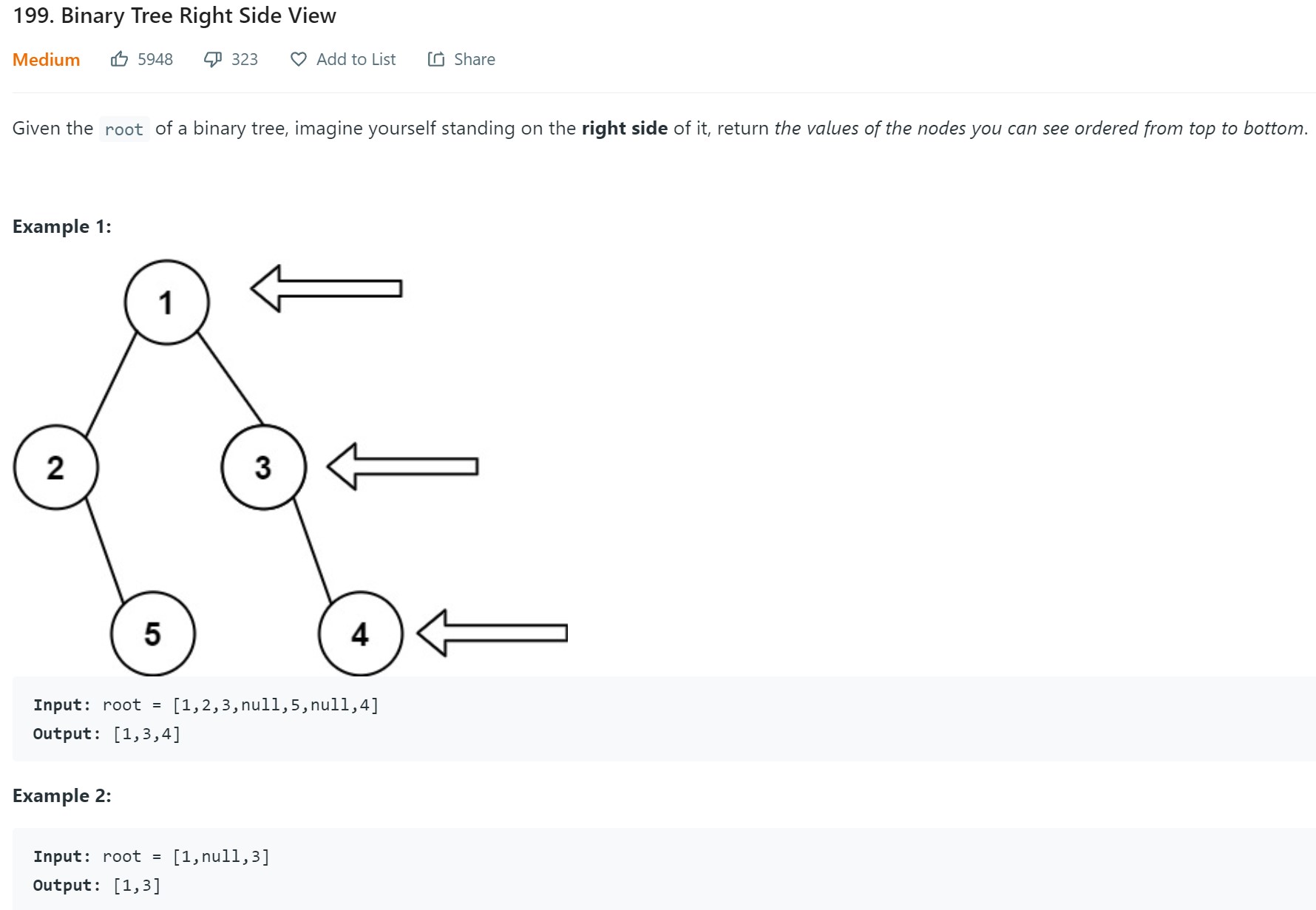
- 3. Binary Tree Right Side View - LC 199 - Medium👏
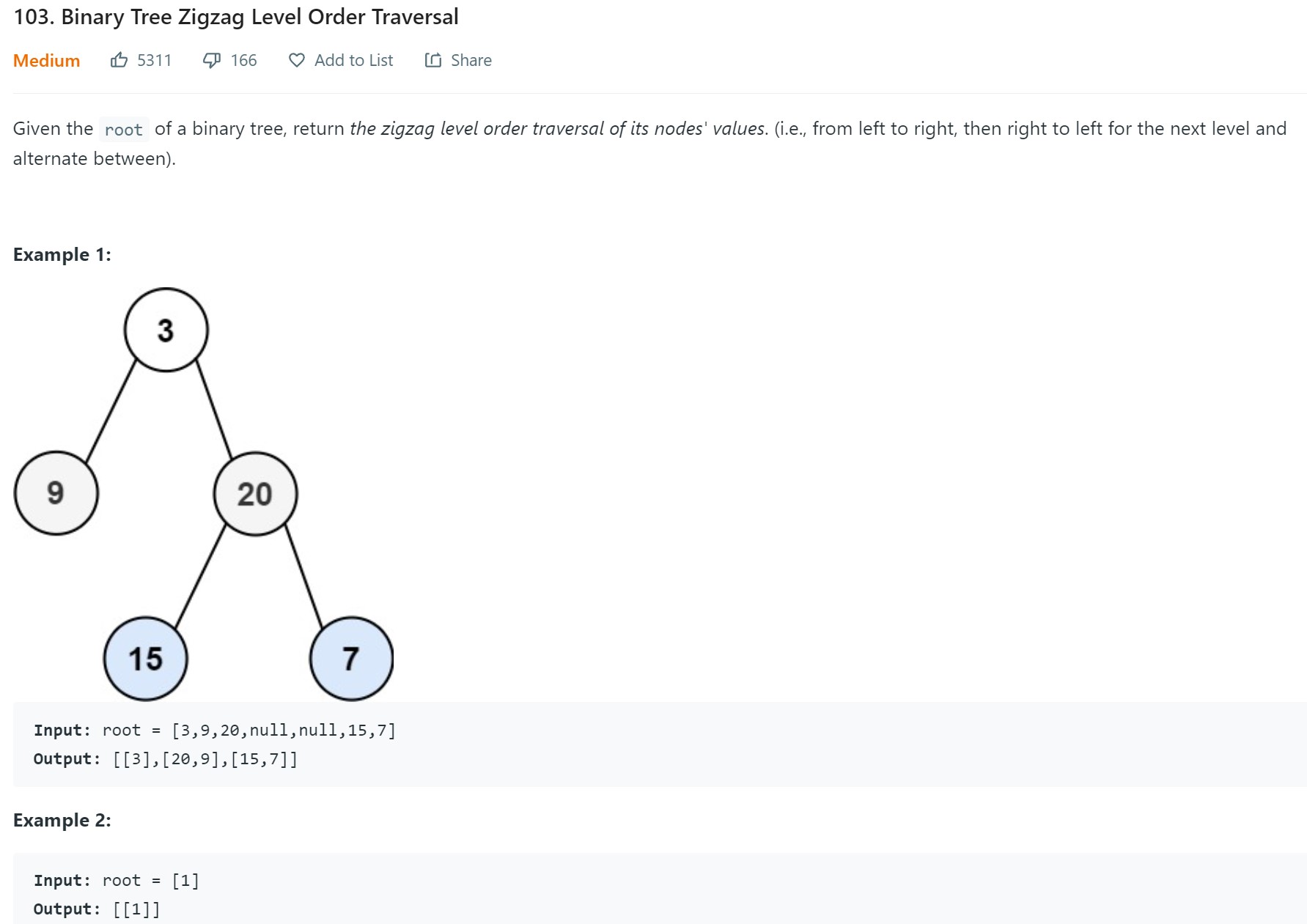
- 4. Binary Tree zig zag level order reversal - LC 103 - Medium😞
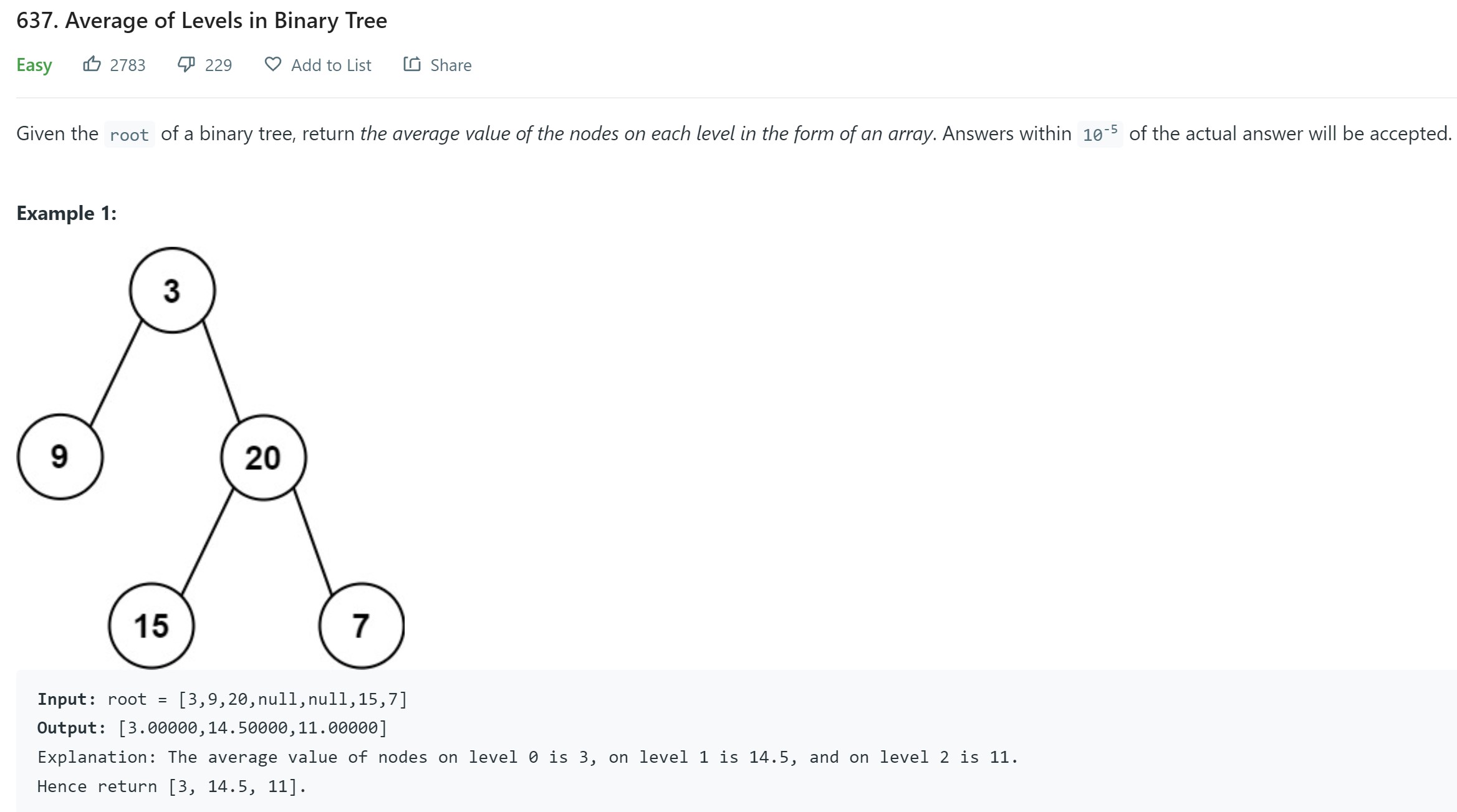
- 5. Average of levels in Binary Tree - LC 637 - Easy
- 6. Minimum Depth of Binary Tree - LC 111 - Easy👏👏
- 7. Maximum Depth of Binary Tree - LC 104 - Easy👏👏
- 8. Maximum width of a Binary Tree - LC 662 - Medium
- 9. Maximum Level sum of a Binary Tree - LC 1161 - Medium👏👏
- 10. Univalued Binary Tree - LC 965 - Easy
- 11. Cousins in a Binary Tree - LC 993 - Easy
- 12. Check completeness of a Binary Tree - LC 958 - Medium
- 13. Find largest value in each tree row - LC 515 - Medium
- 14. Add one row to Tree - LC 623 - Medium
- 15. Same Tree - LC 100 - Easy
- 16. Symmetric Tree - LC 101 - Easy
- 17. Populating next pointers in each node - LC 116 - Medium
- 18. Clone a binary Tree (Not an LC problem)
- Stack
- Top Down DFS
- 1. Path Sum - LC 112 - Easy
- 2. Path Sum II - LC 113 - Medium
- 3. Path Sum III - LC 437 - Medium
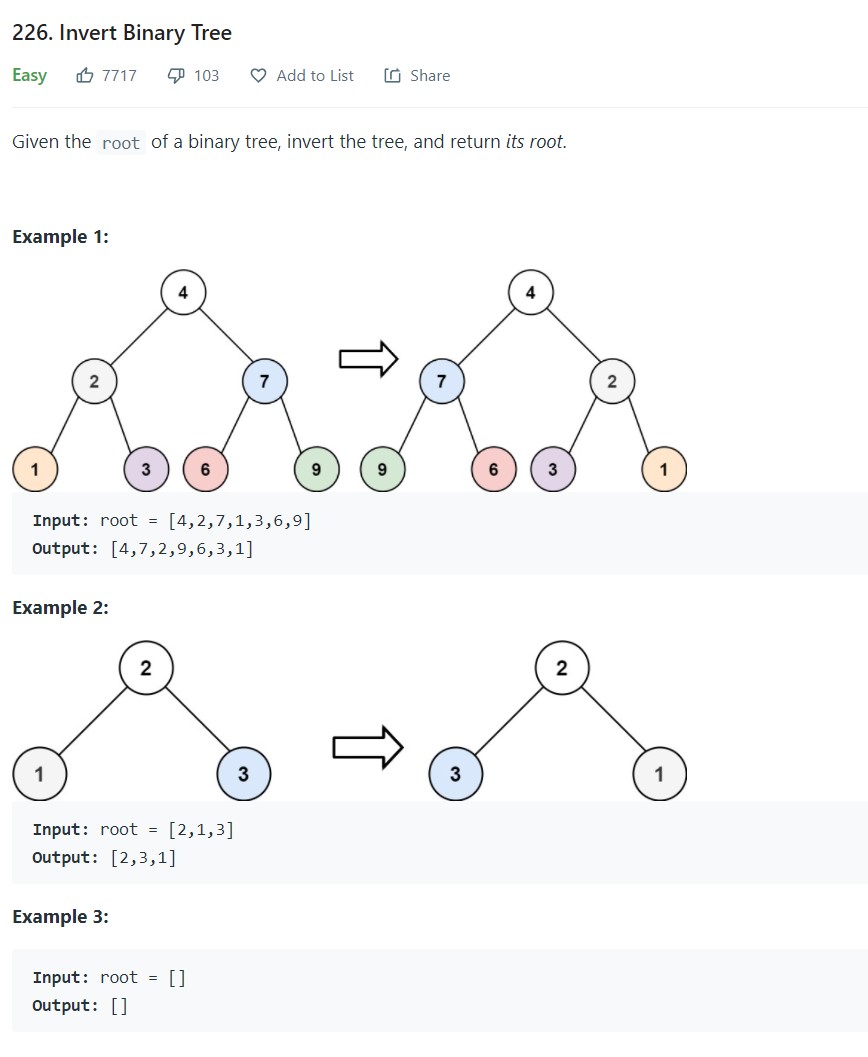
- 4. Invert Binary Tree - LC 226 - Easy
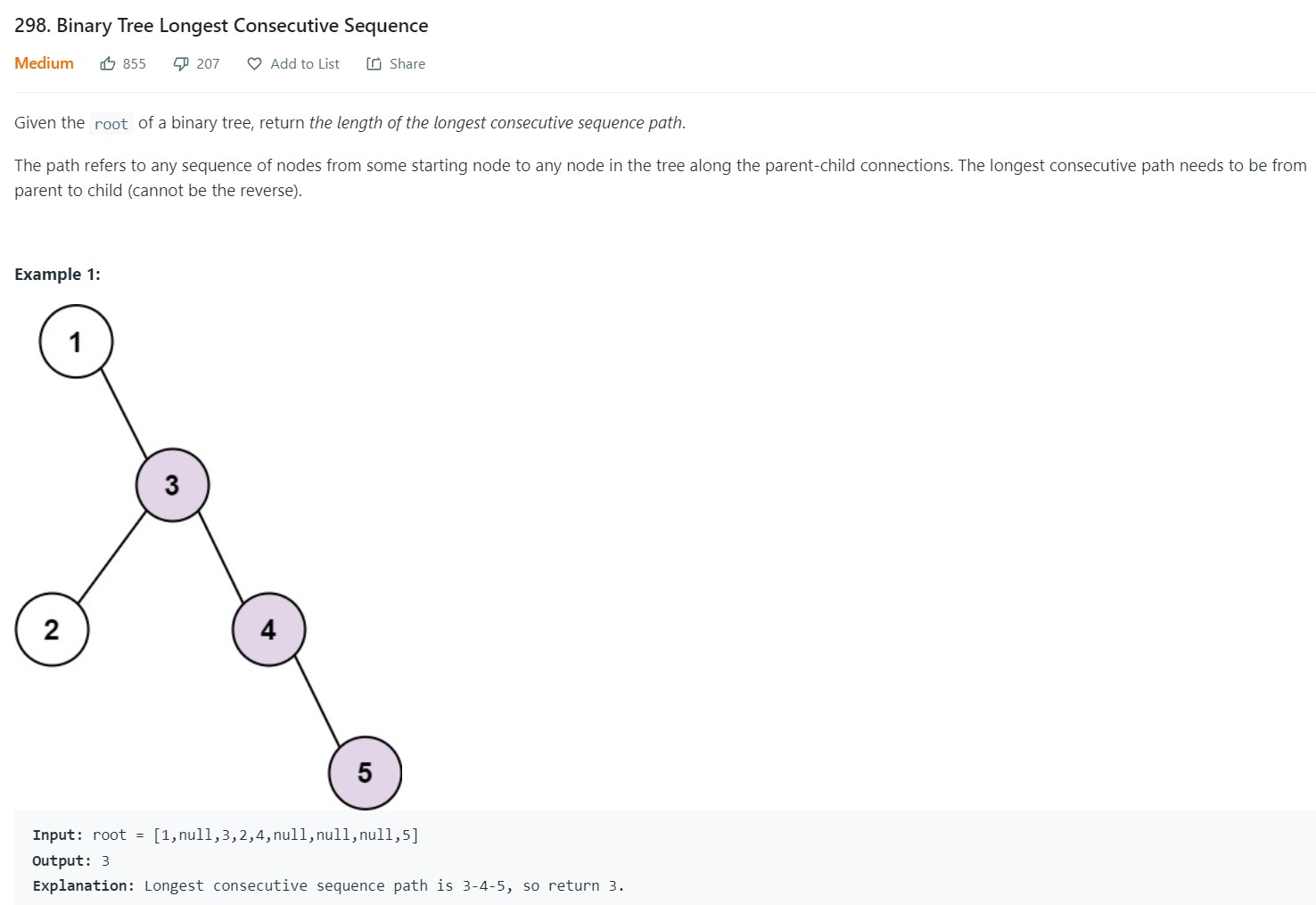
- 5. Binary Tree Longest Consecutive Sequence - LC 298 - Medium
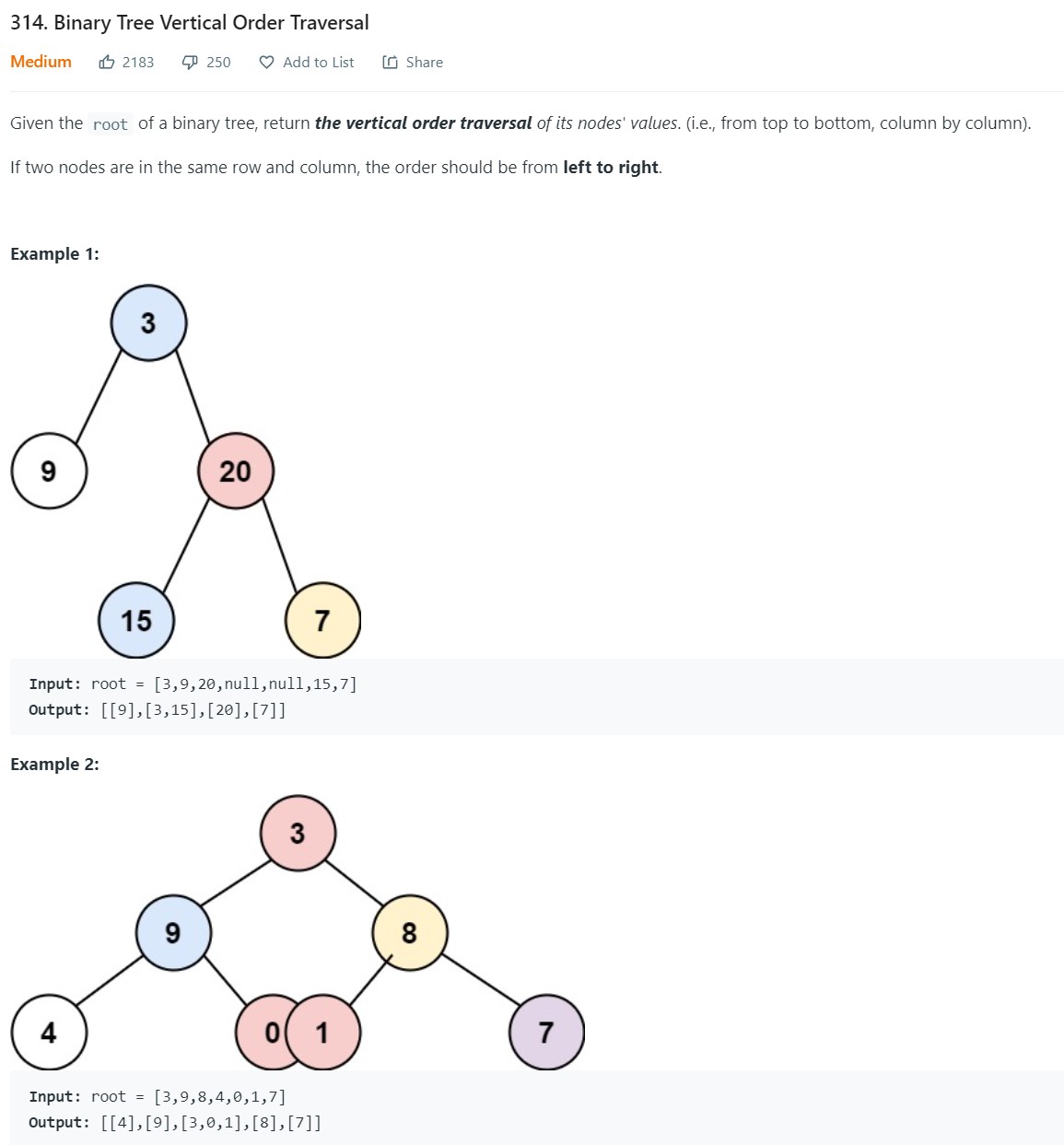
- 6. Binary Tree Vertical Order Traversal - LC 314 - Medium
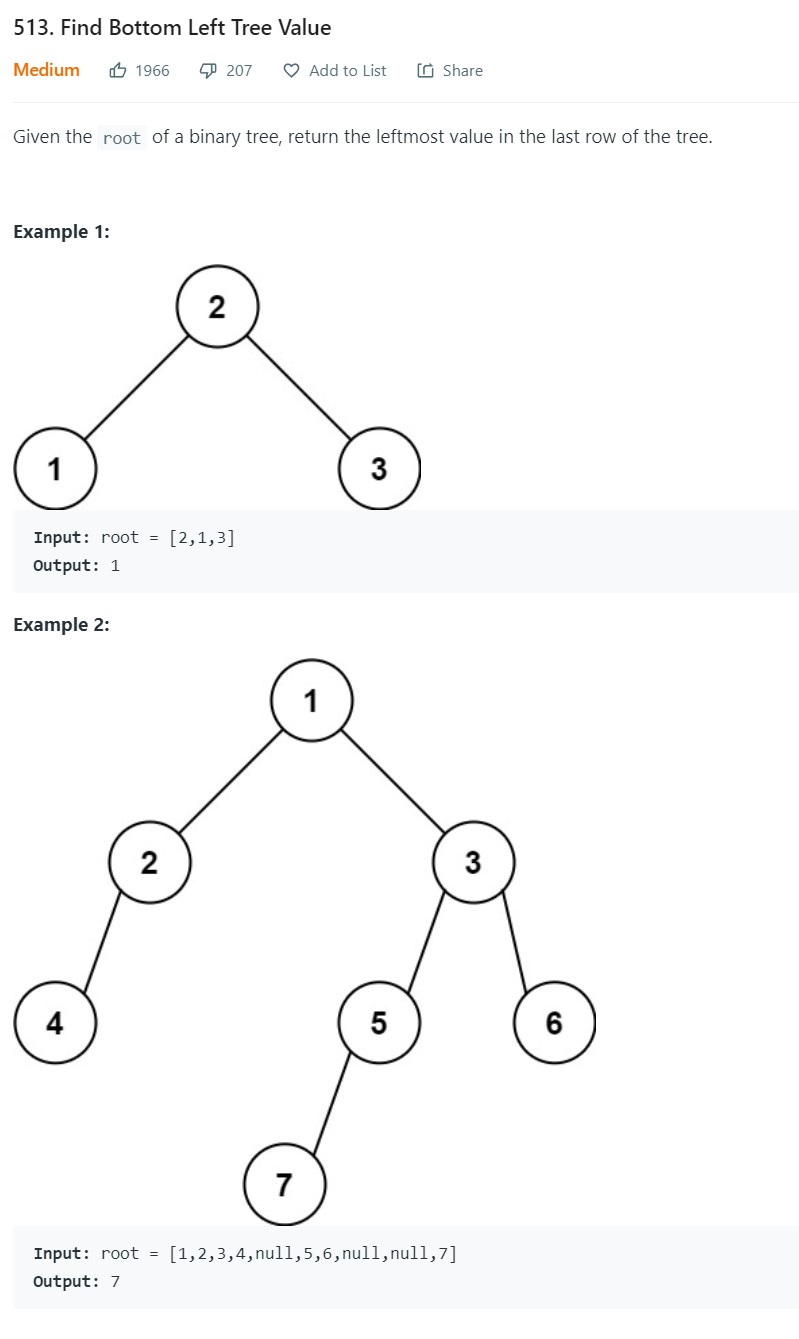
- 7. Find Bottom Left Tree value - LC 513 - Medium
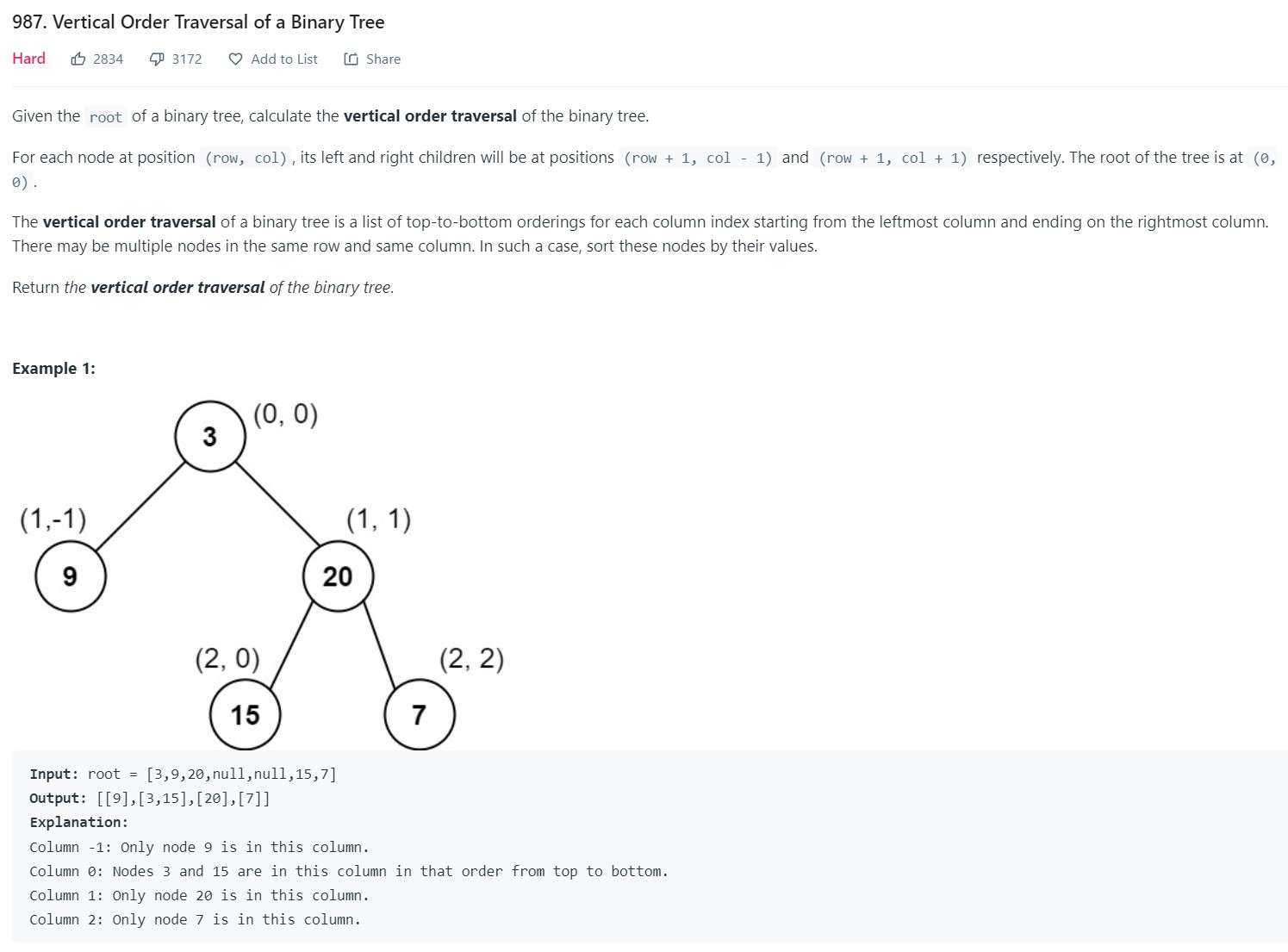
- 8. Vertical Order Traversal of a Binary Tree - LC 987 - Hard
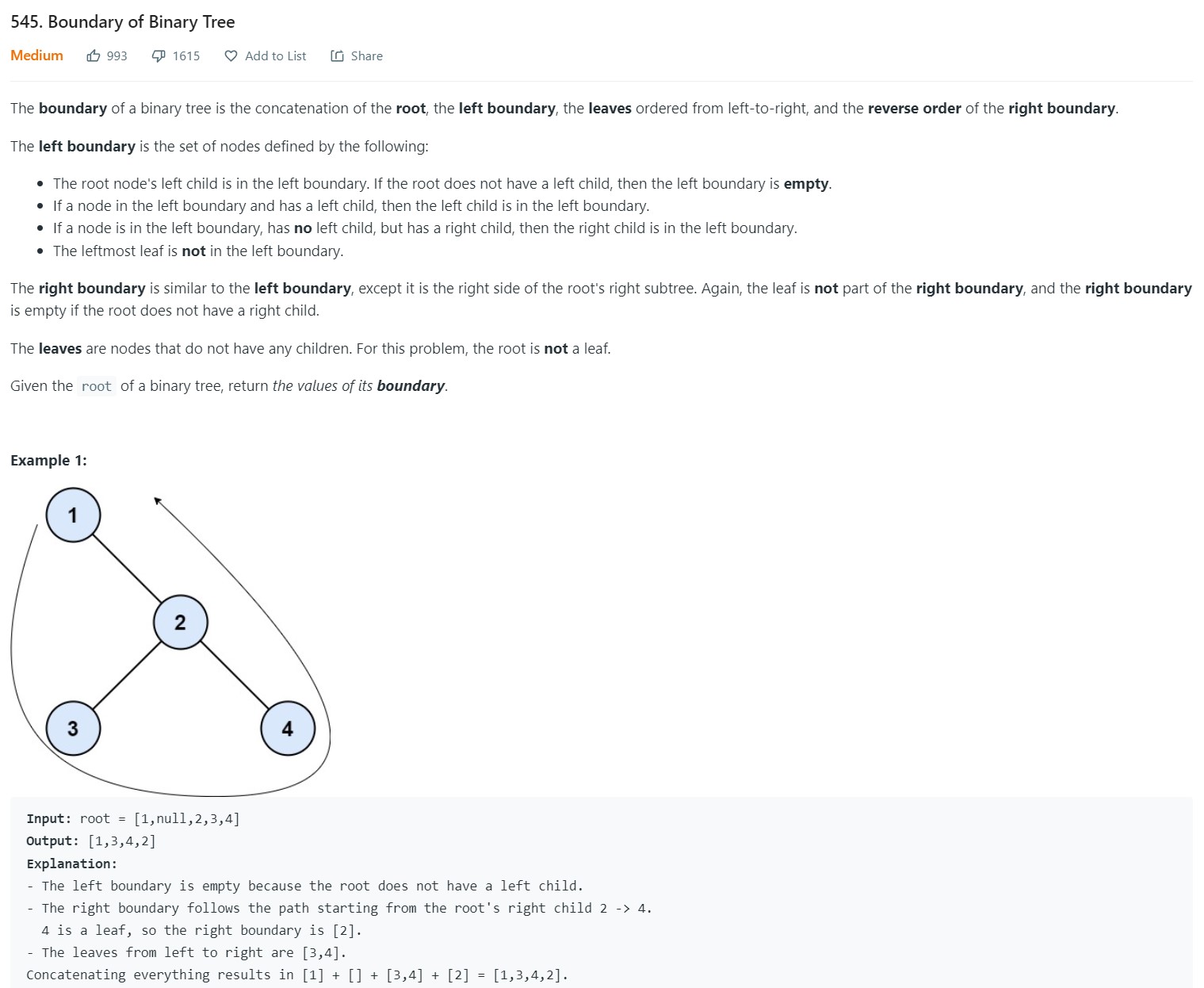
- 9. Boundary of a Binary Tree - LC 545 - Medium
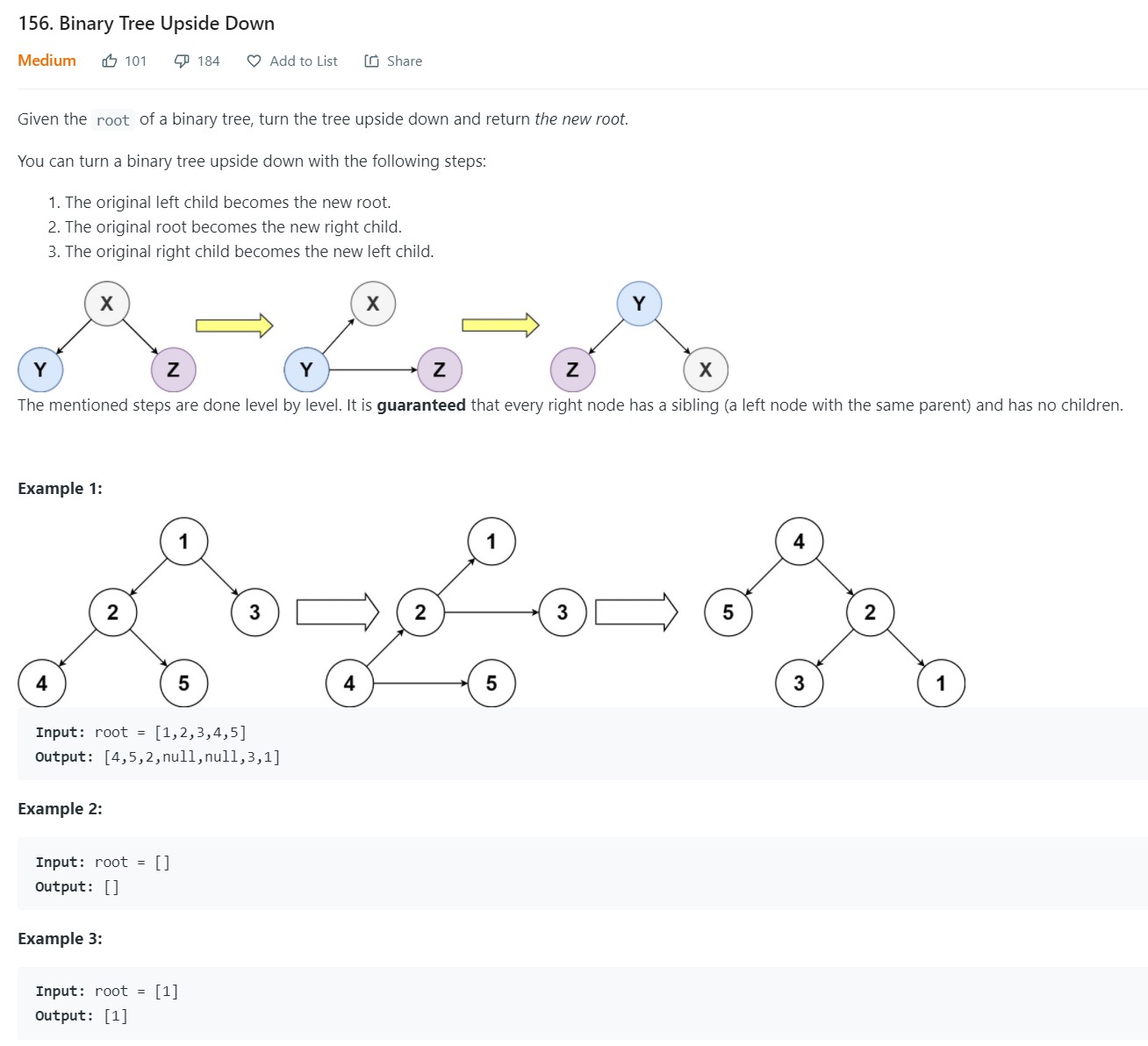
- 10. Binary Tree Upside Down - LC 156 - Medium
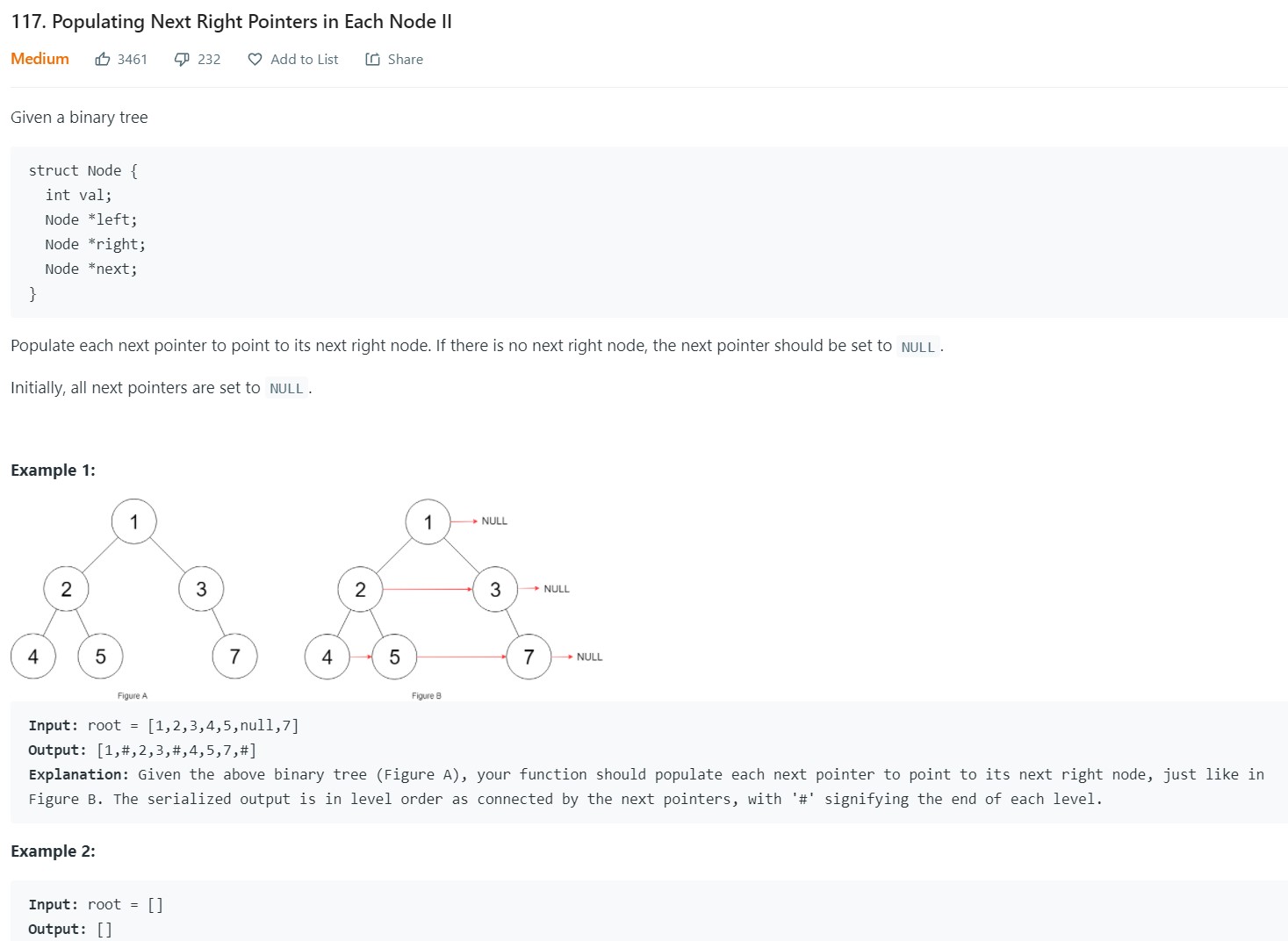
- 11. Populating Next Right Pointers in each Node II - LC 117 - Medium
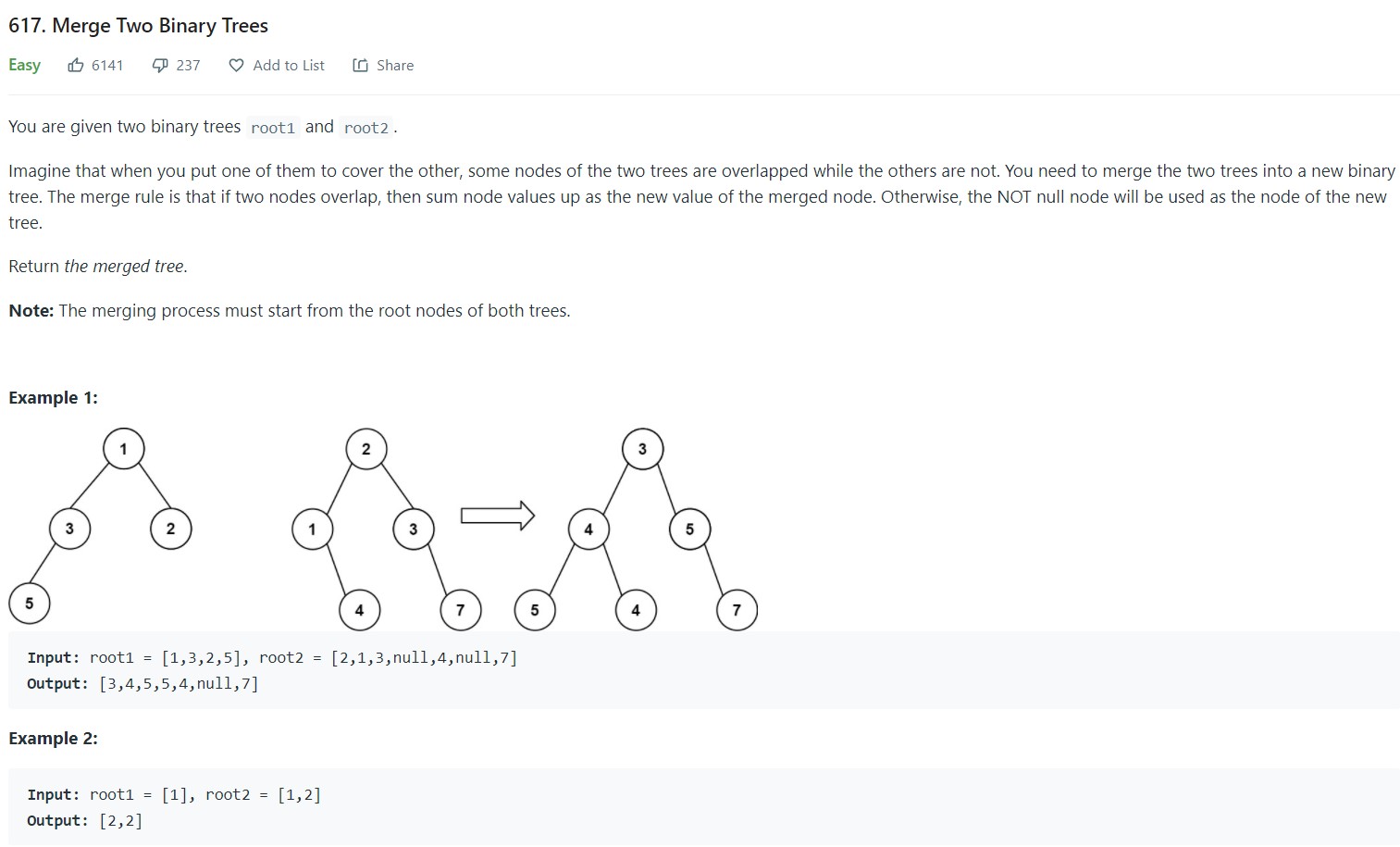
- 12. Merge Two Binary Trees - 617 - Easy
- Bottom Up DFS
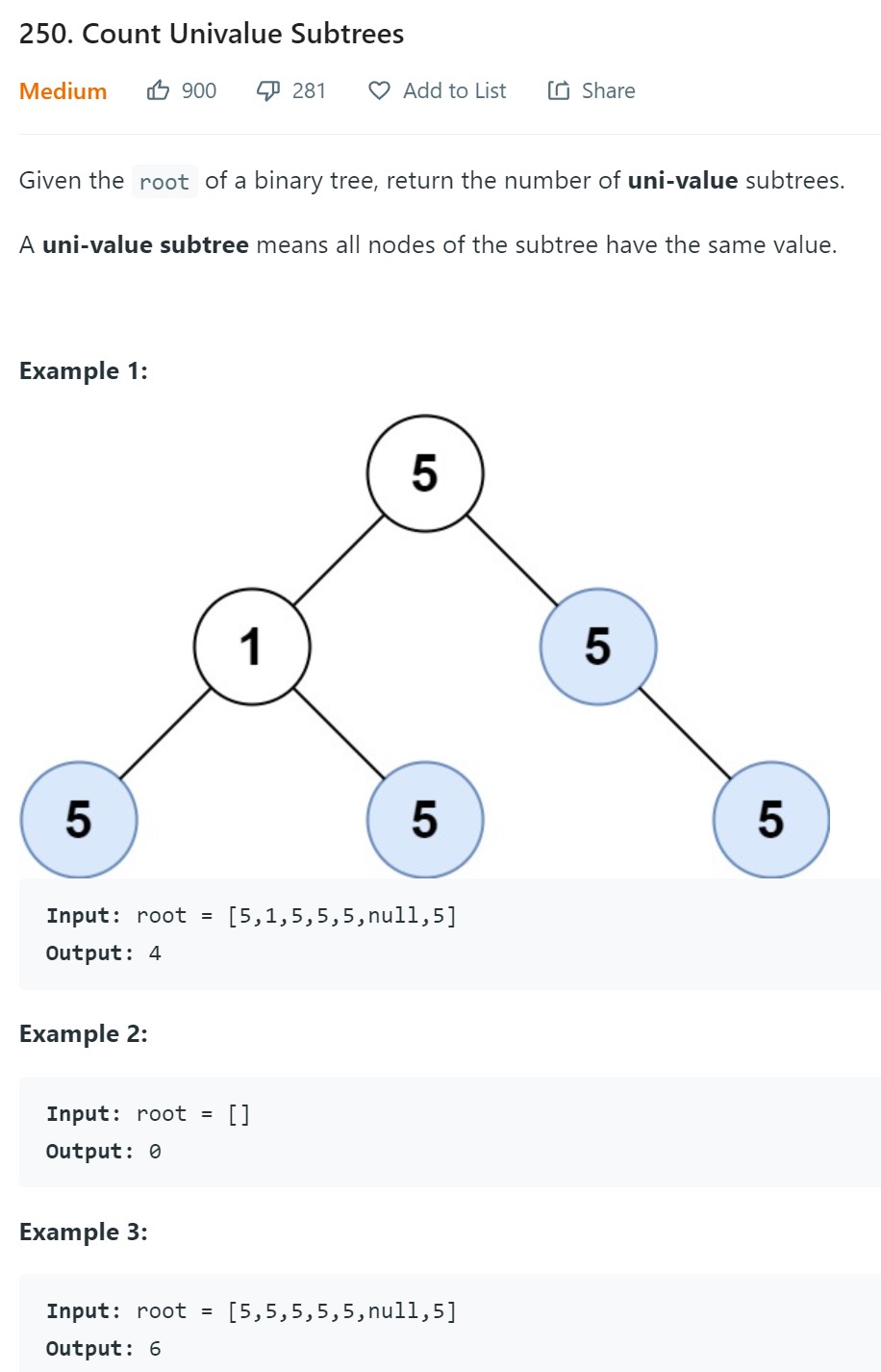
- 1. Count Univalue Subtrees - LC 250 - Medium
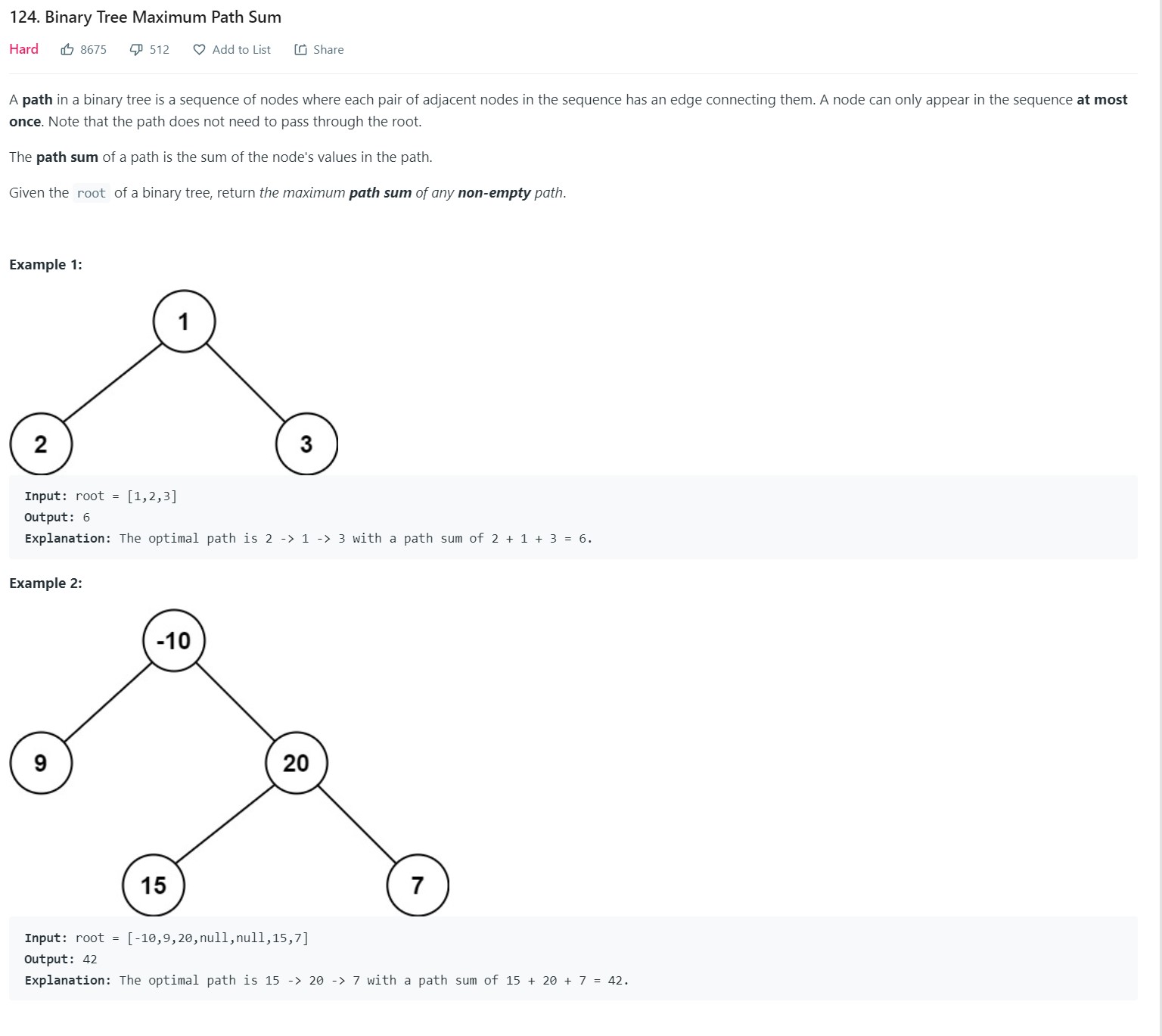
- 2. Binary Tree Maximum Path Sum - LC 124 - Hard
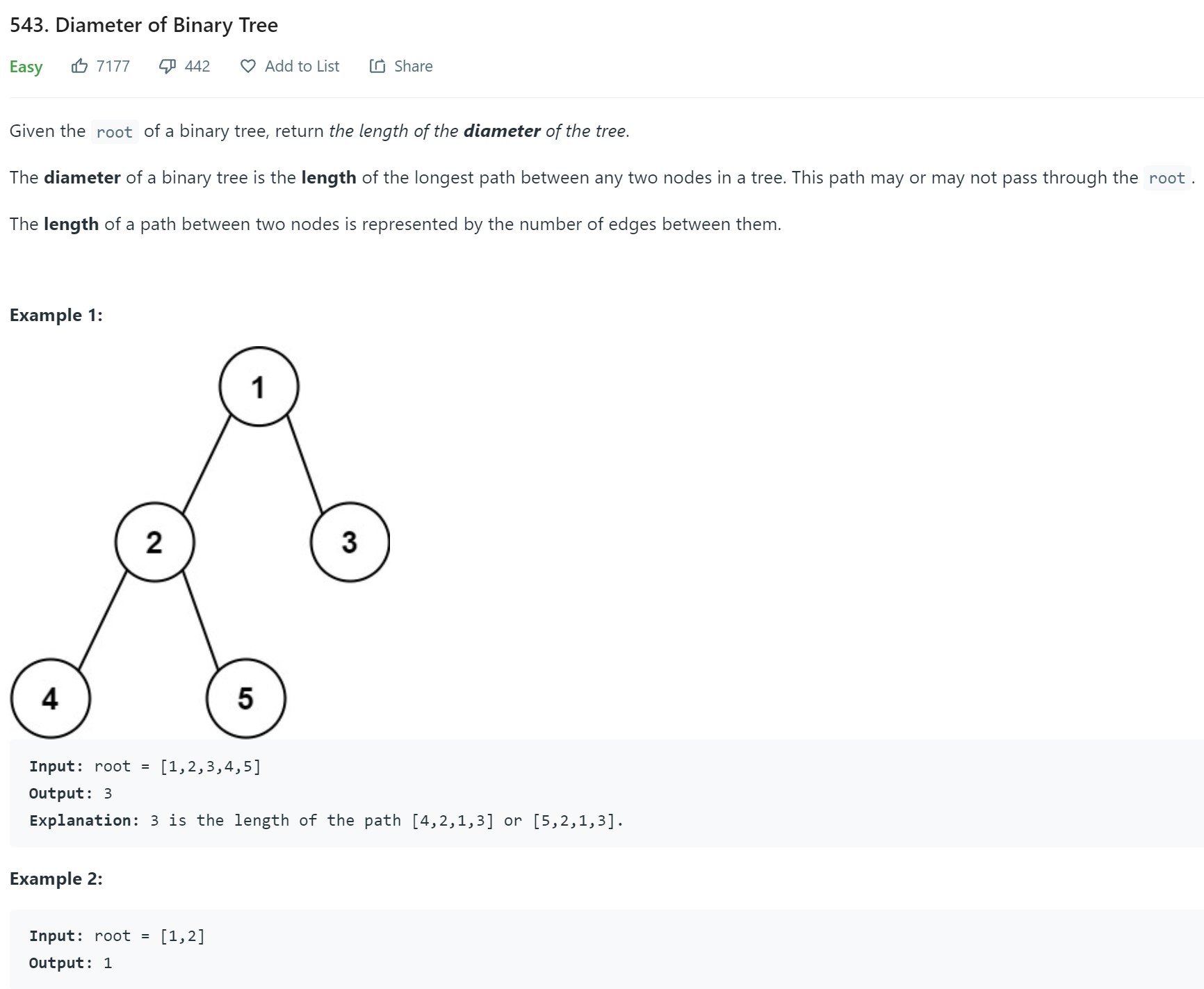
- 3. Diameter of Binary Tree - LC 543 - Easy
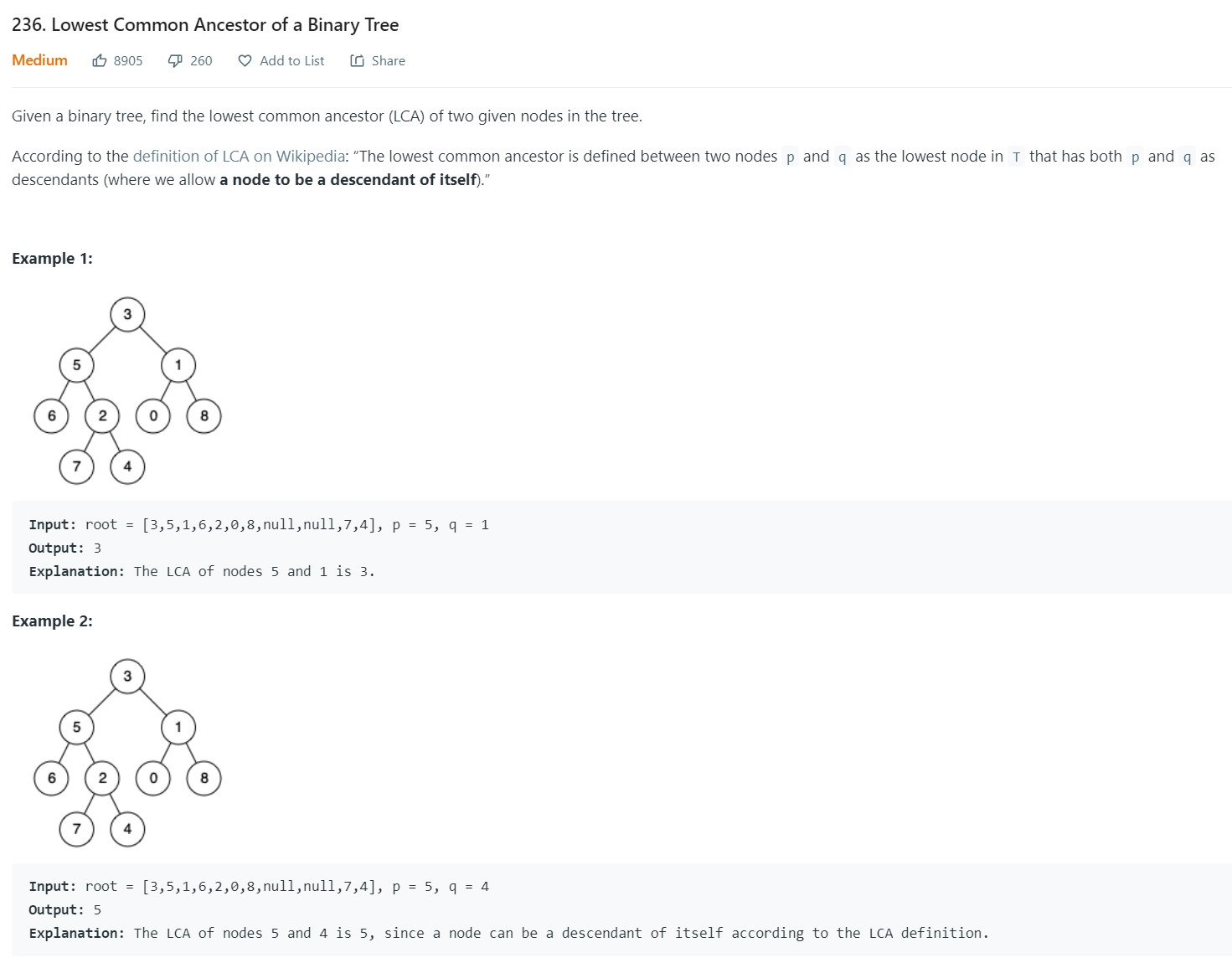
- 4. Lowest Common Ancestor of a binary tree - LC 236 - Medium
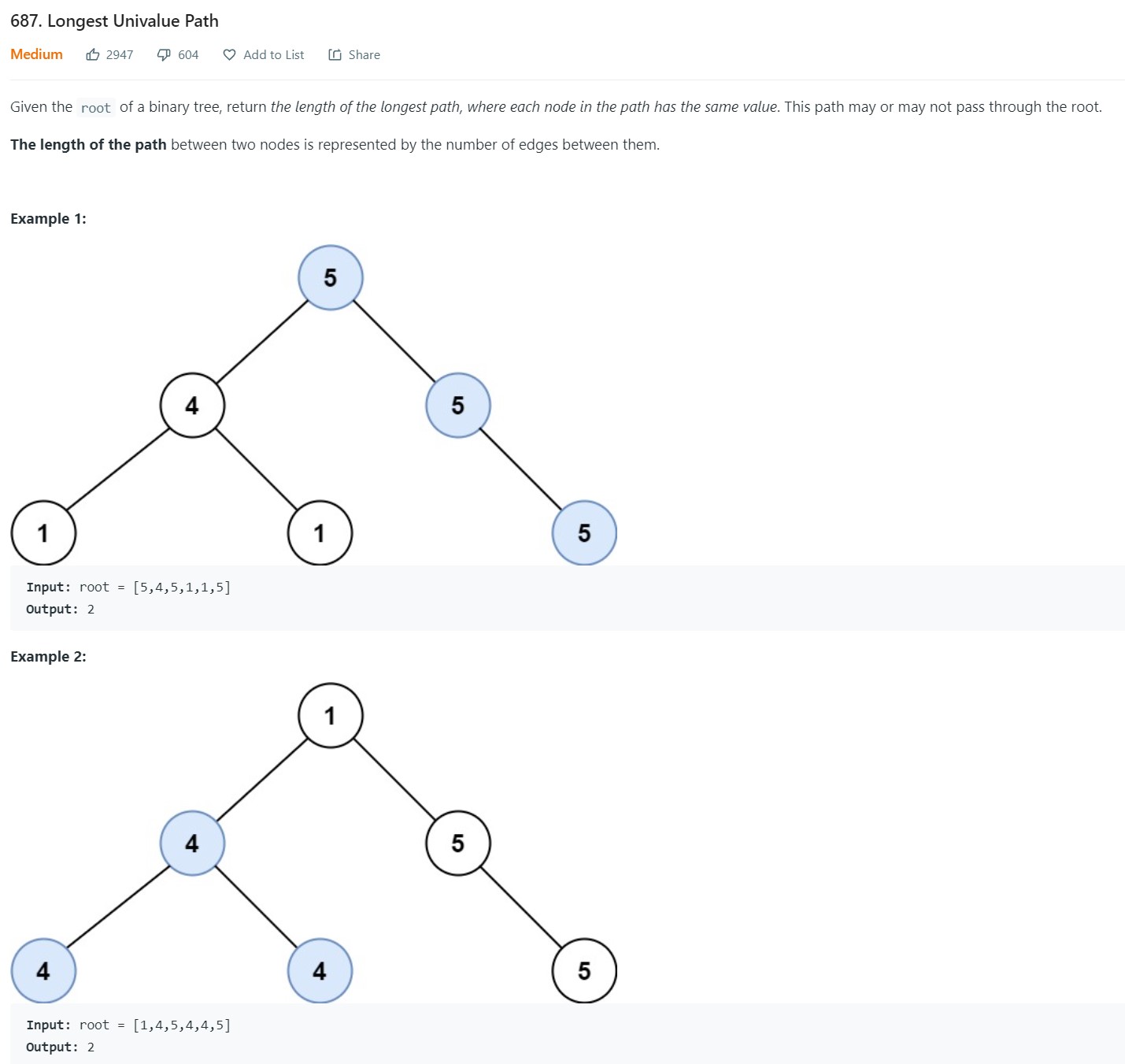
- 5. Longest Unival Path - LC 687 - Medium
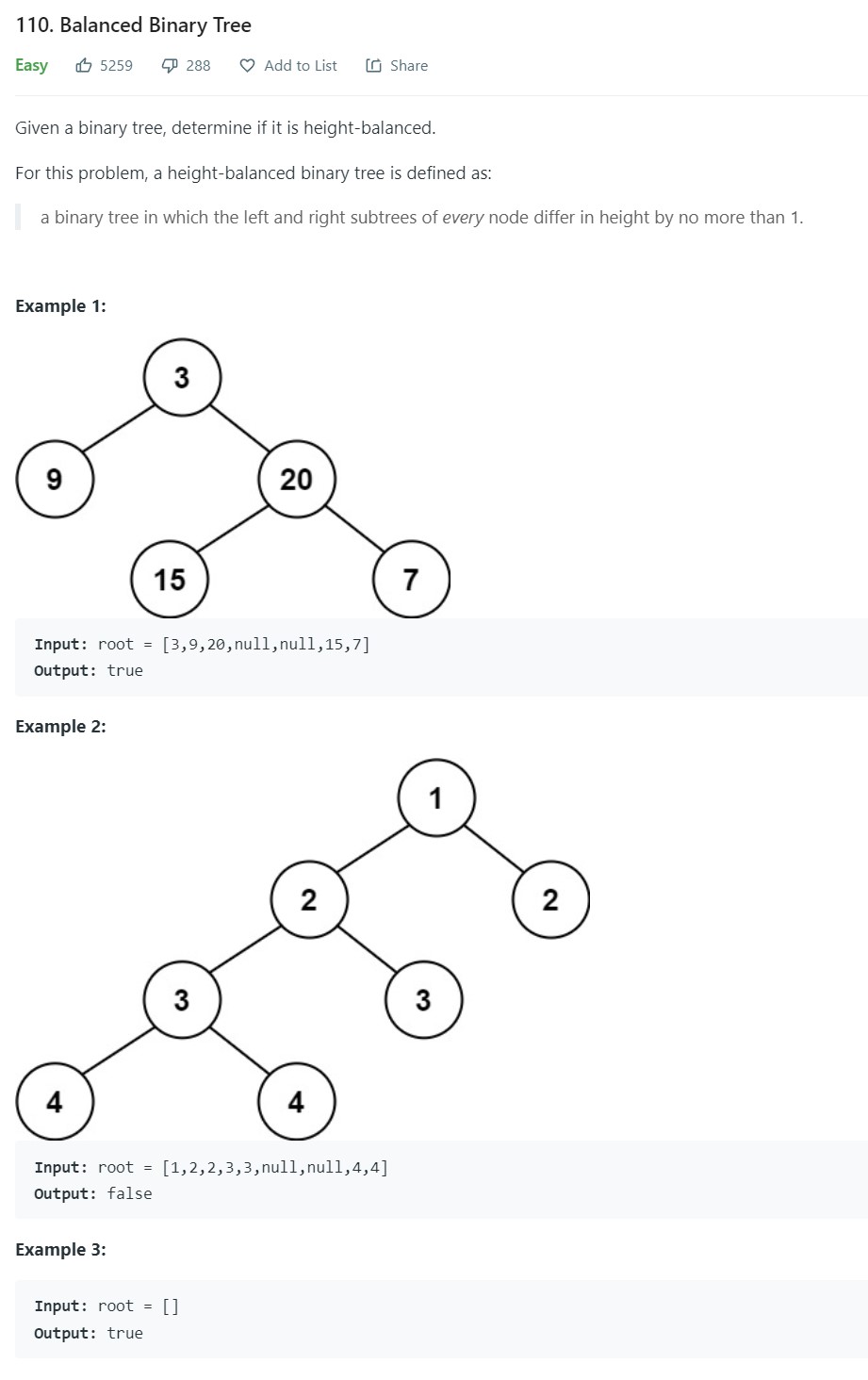
- 6. Balanced Binary Tree - LC 110 - Easy
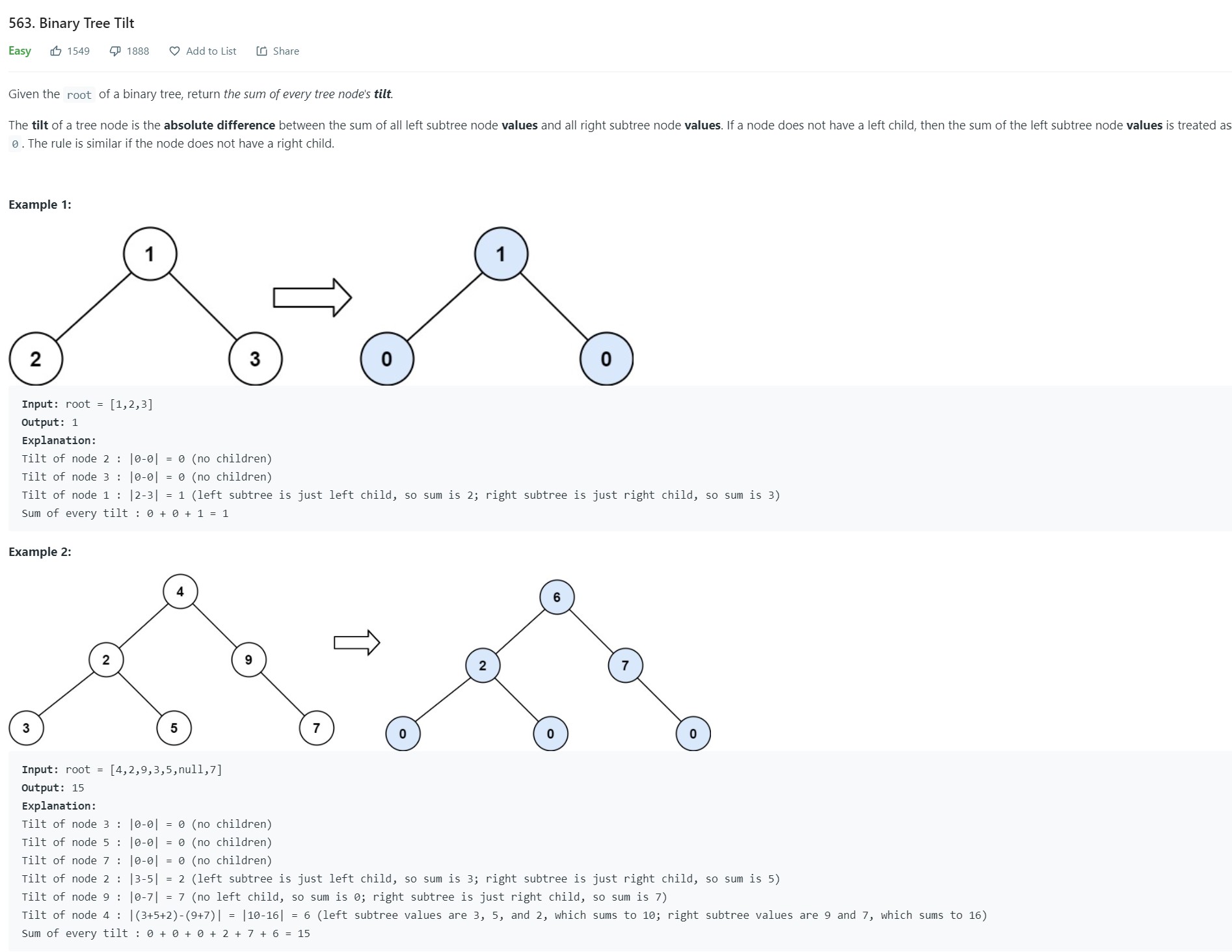
- 7. Binary Tree Tilt - 563 - Easy
- 8. Flatten Binary tree to a linked list - 114 - Medium
- Tree Construction
- Breadth First Search
- Binary Search Tree Problems
- Tree Construction
- 1. Convert sorted array to binary search tree - LC 108 - Easy
- 2. Convert sorted list to BST - 109 - Medium
- 3. Convert BST To Greater Tree - 538 - Medium
- 4. Serialize and Deserialize BST - 449 - Medium
- 5. Constrct BST from preorder traversal - 1008 - Medium
- 6. Merge Two BSTs to sorted lists [IK problem]
- 7. Merge two BSTs [EPI problem]
- Bottom Up DFS
- 1. Convert BST to sorted doubly linked list - 426 - Medium
- 2. Largest BST Subtree - LC 333 - Medium
- 3. Kth smallest element in a BST - 230 - Medium
- 4. Binary Search Tree Iterator - 173 - Medium
- 5. Increasing Order Search Tree - 897 - Easy
- 6. Recover Binary Search Tree - 99 - Medium
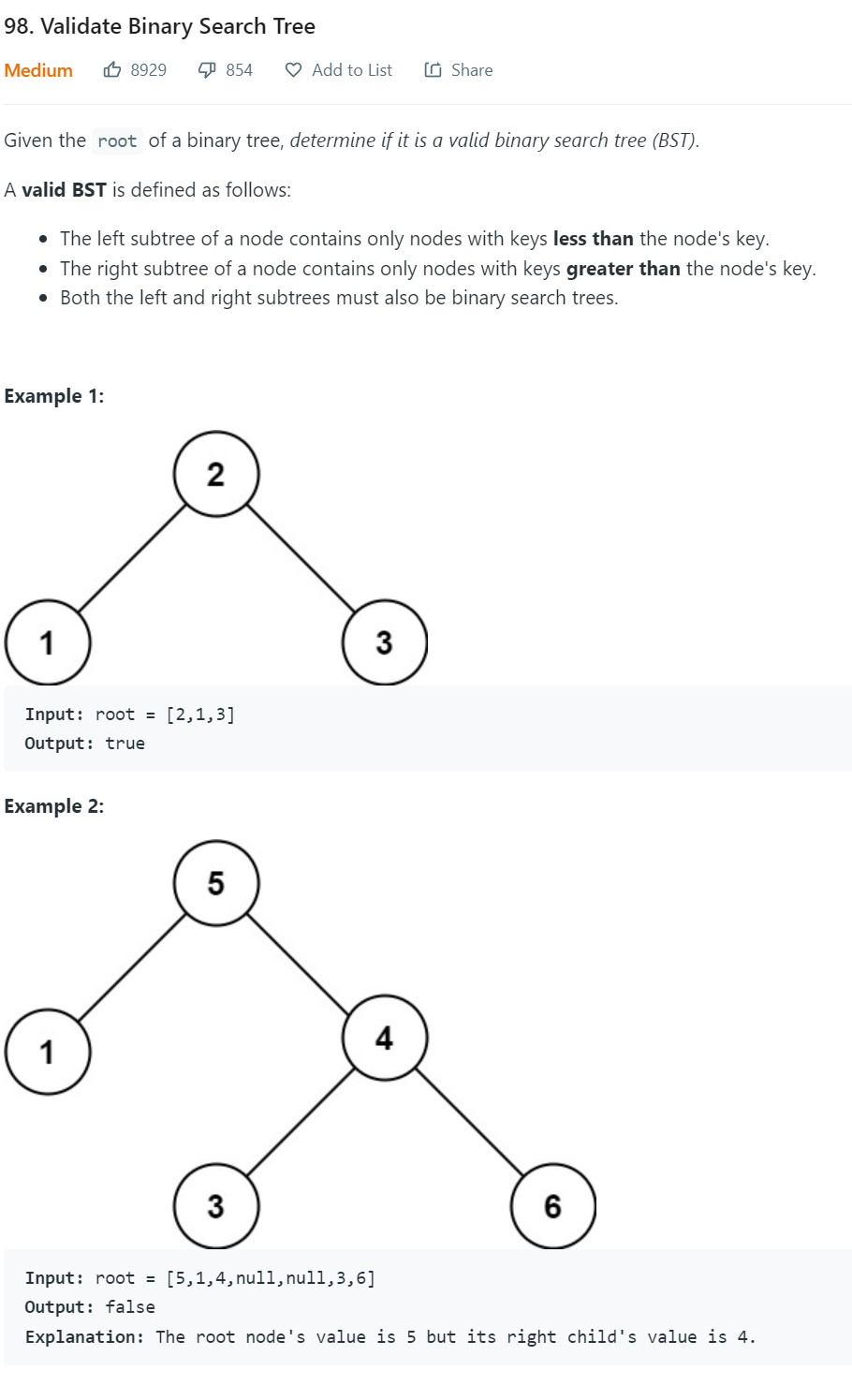
- 7. Validate Binary Search Tree - LC 98 - Medium
- Tree Construction
- N-Aray Tree Problems
- References:
Binary Tree Problems
Practice Score
| Emoji | Meaning |
|---|---|
| 👏 | # of times practiced |
| 😎 | Ten claps in a row |
Breadth First Search
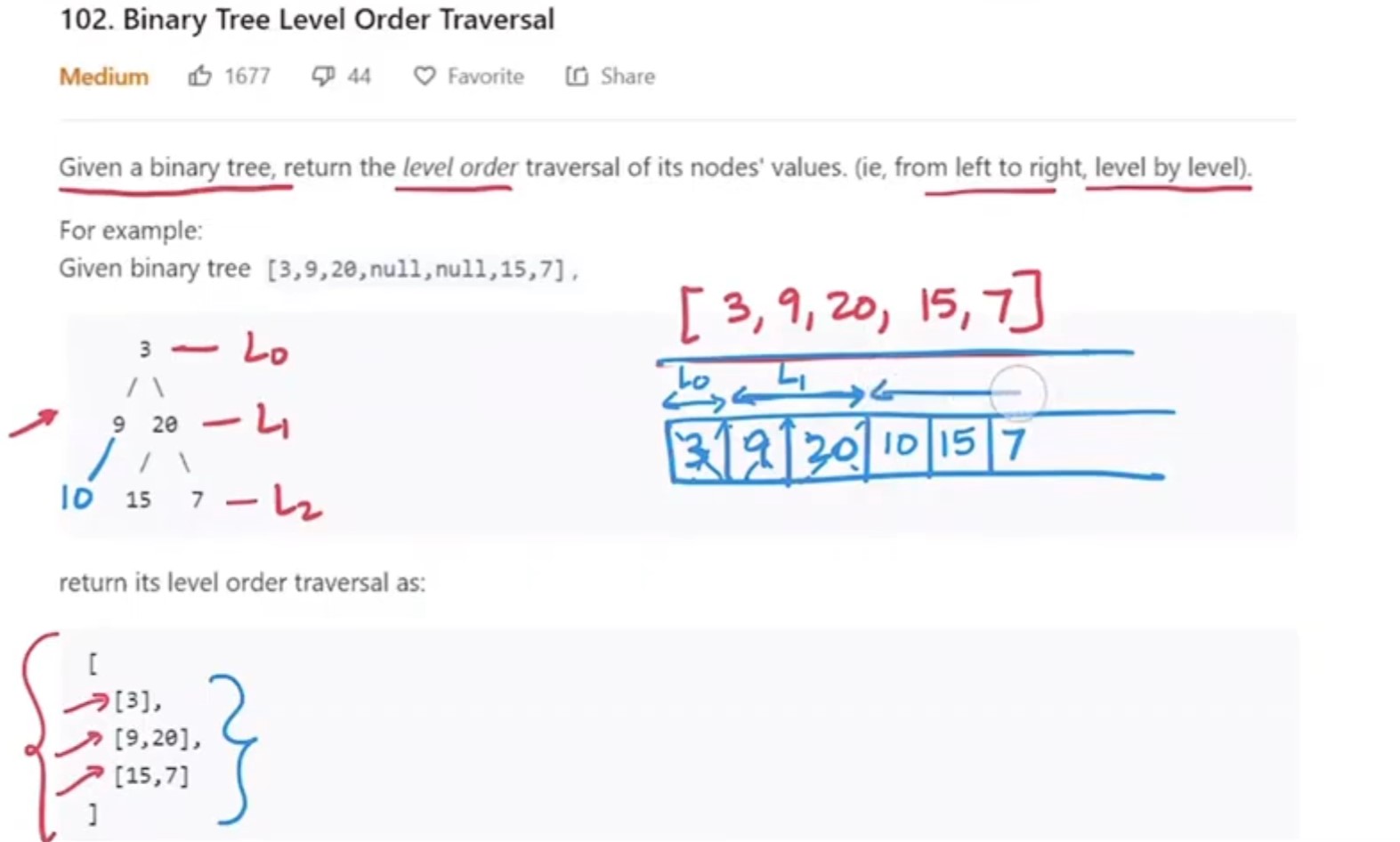
1. Binary Tree Level Order Traversal - LC 102 - Medium 👏👏👏👏👏👏👏👏👏👏
Video Reference":“Alternative Class -Trees With Omkar: 14:06 hour
-
Code
- The tricky part of this question is to group the output at each level as inner list. This means we need a way to know which ones belong to each level.
- We could keep track of this using a hash table, or another queue. The approach in this solution is to take a snapshot of the queue at each level and add the entries to a sublist which is then appended to the global list.
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]: if root is None: return [] result = [] q = collections.deque([root]) # When I tried while q is not None: leetcode gave me error memory exceeded. # Looks like we need to check explicitly for len != 0. IMPORTANT!!! while len(q) != 0: numnodes = len(q) temp = [] for _ in range(numnodes): node = q.popleft() temp.append(node.val) if node.left is not None: q.append(node.left) if node.right is not None: q.append(node.right) result.append(temp) return result
-
Points to Note
- With mutable approach, leaf level always does the cloning, so focus on them for total compelxity. internal worker only adds to the slate...so contstant amortized time - In a complete binary tree, the number of leaf nodes is equal to the number of internal nodes excluding the 1. 50% of nodes are leaf nodes. - Do not check for `while q is not None:`. Leetcode gave the error memory exceeded. Explicitly check for `len(q) !=0` - When root is added to dequeue, add it as list. `[root]`. Otherwise LC gives error
-
Complexity Analysis
- In tree problems even though we see loop within a loop, the inner loop can many times do only constant work. In this problem, the total time and space complexity is O(N) even though it may appear that we have loop within a loop. The inner loop is doing constant work of push and pop and the outer loop goes through all the nodes which is O(N).
2. Binary Tree Level order traversal II - LC 107 - Medium
- Video Reference: “Alternative Class -Trees With Omkar: 1:02:20 hours”,
-
Code
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]: if root is None: return [] q = deque([root]) result = [] while len(q): temp = [] numnodes = len(q) for _ in range(numnodes): node = q.popleft() temp.append(node.val) if node.left is not None: q.append(node.left) if node.right is not None: q.append(node.right) result.append(temp) result.reverse() return result
-
Points to Note
-
It is very important to know where to call the reverse() function.
- if temp.reverse() is called, then it reverses the elements within each list
- if result.reverse() is called right after result.append(temp), then it reverses in between lists
- result.reverse() should be called right after the outmost loop just before the return statement.
-
We could use a stack to store it and pop the results out at the end to reverse the list
-
We could use a two sided dequeue
-
Could we insert into an array from the left instead of right? This may not be a constant time operation so we may have to use a linked list.
-
The simplest approach could be just to reverse the list at the end. This reverses the outer sub lists but not the elements within the list. The elements are still from left to right but the levels are from bottom to top.
-
-
Complexity
- There is no change to the complexity. The reverse operation is also of O(N) time.
3. Binary Tree Right Side View - LC 199 - Medium
-
Code
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def rightSideView(self, root: Optional[TreeNode]) -> List[int]: if root is None: return [] result = [] q = deque([root]) while len(q): numnodes = len(q) for _ in range(numnodes): child = q.popleft() temp = child.val if child.left is not None: q.append(child.left) if child.right is not None: q.append(child.right) result.append(temp) return result
-
Points to Note
-
We could use the same template and return temp[-1] to return the rightmost element. Or we could just rename temp as a variable and overwrite the values so that it holds the last value in each level which is the rightmost.
-
Why is the recursion tree is of size O(2^N.N) whereas we say here it is of O(N)? In the recursion class, the size of the input is small because all these have exponential time complexity with the input size and results in huge tree. The height is O(N) because at each level only one blank is filled. At leaf level the entire subset or permutation is created which is added to global result.
The height is O(N) total number of nodes is exponential in N, because we have 2^N leaf nodes (even if branching factor is 2).
In the trees problem, N is not the height of the tree, it is the total number of nodes in the tree.
-
-
Complexity
- There is no change to the complexity. The reverse operation is als of O(N) time.
4. Binary Tree zig zag level order reversal - LC 103 - Medium
-
Code
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def zigzagLevelOrder(self, root: Optional[TreeNode]) -> List[List[int]]: if root is None: return [] q = deque([root]) result = [] right_to_left = False while len(q): numnodes = len(q) temp = [] for _ in range(numnodes): node = q.popleft() temp.append(node.val) if node.left is not None: q.append(node.left) if node.right is not None: q.append(node.right) if right_to_left: temp.reverse() right_to_left = not right_to_left result.append(temp) return result
-
Points to Note
-
right_to_left = not right_to_left. The other way to write this is if right_to_left is True: right_to_left = False else: right_to_left = True
-
For trees and graphs, the complexity is mostly linear if BFS is used of O(N).
-
Complexity:
- There is no change to the complexity. It is of O(N) time.
-
-
Coding Mistakes
2022-02-28: 😟
- The right_to_left flag used to track alternate zigzag order was initialized inside the first loop. It should have been initialized outside all the loops. The first loop (while len(q)) is used to gather all the nodes in the tree. The inner for _ in len(numnodes) is used to gather all the children. Since we need to reverse the order at every level, the flag should be outside the while loop and not outside the for loop.
- Took 11 minutes 3 seconds.
5. Average of levels in Binary Tree - LC 637 - Easy
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]: if root is None: return [] result = [] q = deque([root]) while len(q): numnodes = len(q) total = 0 for _ in range(numnodes): node = q.popleft() total += node.val if node.left is not None: q.append(node.left) if node.right is not None: q.append(node.right) avg = total / numnodes result.append(avg) return result
- Complexity Analysis
6. Minimum Depth of Binary Tree - LC 111 - Easy
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def minDepth(self, root: Optional[TreeNode]) -> int: if root is None: return 0 min_depth = 0 q = deque([root]) while len(q): numnodes = len(q) min_depth += 1 for _ in range(numnodes): node = q.popleft() if node.left is None and node.right is None: return min_depth if node.left is not None: q.append(node.left) if node.right is not None: q.append(node.right)
- Complexity Analysis
-
Coding Mistakes
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20class Solution: def minDepth(self, root: Optional[TreeNode]) -> int: if root is None: return 0 min_depth = 0 q = deque([root]) while len(q): numnodes = len(q) min_depth += 1 # 2022-02-28: The count is incremented outside the for loop ...not inside for _ in range(numnodes): node = q.popleft() if node.left is None and node.right is None: return min_depth if node.left is not None: q.append(node.left) if node.right is not None: q.append(node.right)
7. Maximum Depth of Binary Tree - LC 104 - Easy
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def maxDepth(self, root: Optional[TreeNode]) -> int: if root is None: return 0 q = deque([root]) maxdepth = 0 while len(q): numnodes = len(q) maxdepth += 1 for _ in range(numnodes): node = q.popleft() if node.left is not None: q.append(node.left) if node.right is not None: q.append(node.right) return maxdepth
- Complexity Analysis
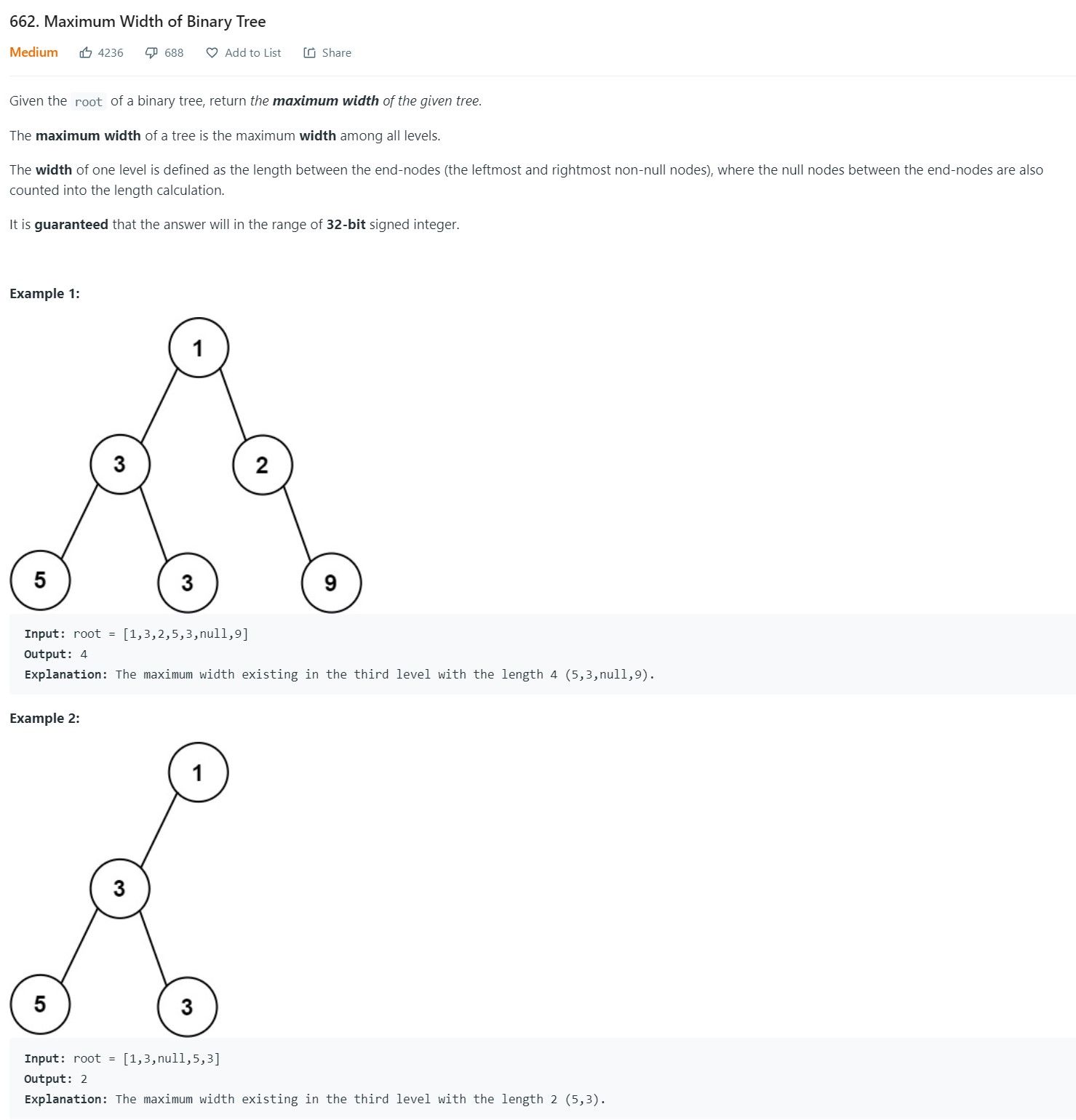
8. Maximum width of a Binary Tree - LC 662 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int: if root is None: return 0 q = deque([(root, 1)]) maxwidth = 0 while len(q): numnodes = len(q) first = last = None for _ in range(numnodes): (node, id) = q.popleft() if node.left is not None: q.append((node.left, 2*id)) if node.right is not None: q.append((node.right, 2*id+1)) last = id if first is None: first = id maxwidth = max(maxwidth, last-first+1) return maxwidth
- Complexity Analysis
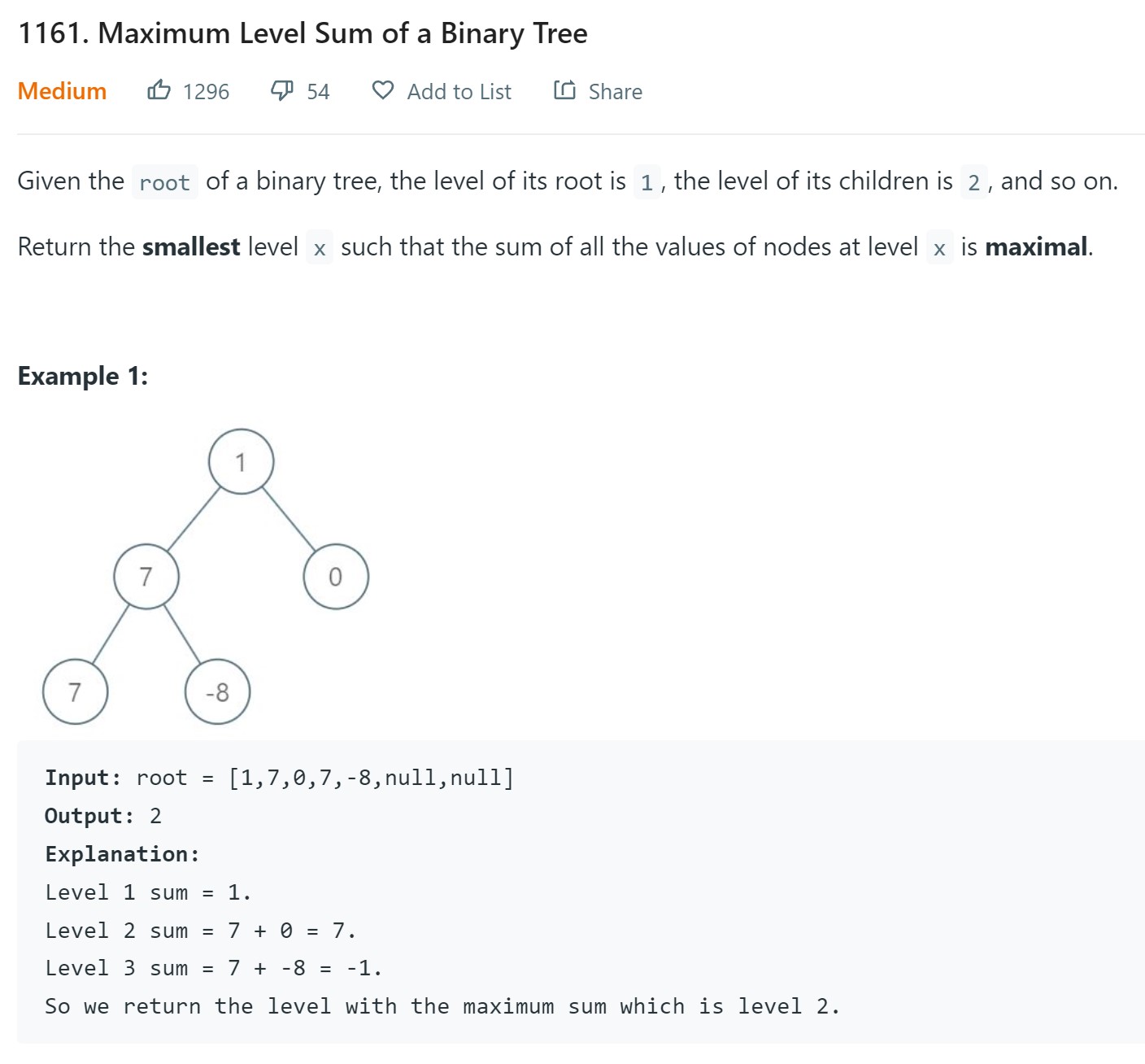
9. Maximum Level sum of a Binary Tree - LC 1161 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def maxLevelSum(self, root: Optional[TreeNode]) -> int: if root is None: return 0 sum = float(-inf) min_level = 0 level = 0 q = deque([root]) while len(q): numnodes = len(q) total = 0 level += 1 for _ in range(numnodes): node = q.popleft() total += node.val if node.left is not None: q.append(node.left) if node.right is not None: q.append(node.right) if sum < total: sum = total min_level = level return min_level
- Complexity Analysis
10. Univalued Binary Tree - LC 965 - Easy
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def isUnivalTree(self, root: Optional[TreeNode]) -> bool: if root is None: return False q = deque([root]) while len(q): node = q.popleft() if node.left is not None and node.right is not None: if node.left.val != node.right.val: return False if node.left.val != node.val: return False if node.left is not None: q.append(node.left) if node.left.val != node.val: return False if node.right is not None: q.append(node.right) if node.right.val != node.val: return False return True
- Complexity Analysis
11. Cousins in a Binary Tree - LC 993 - Easy
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def isCousins(self, root: Optional[TreeNode], x: int, y: int) -> bool: if root is None: return False q = deque([root]) while len(q): numnodes = len(q) px, py = None, None for _ in range(numnodes): node = q.popleft() if node.left is not None: q.append(node.left) if node.left.val == x: px = node.val if node.left.val == y: py = node.val if node.right is not None: q.append(node.right) if node.right.val == x: px = node.val if node.right.val == y: py = node.val if px is not None and py is not None and px != py: return True return False
- Complexity Analysis
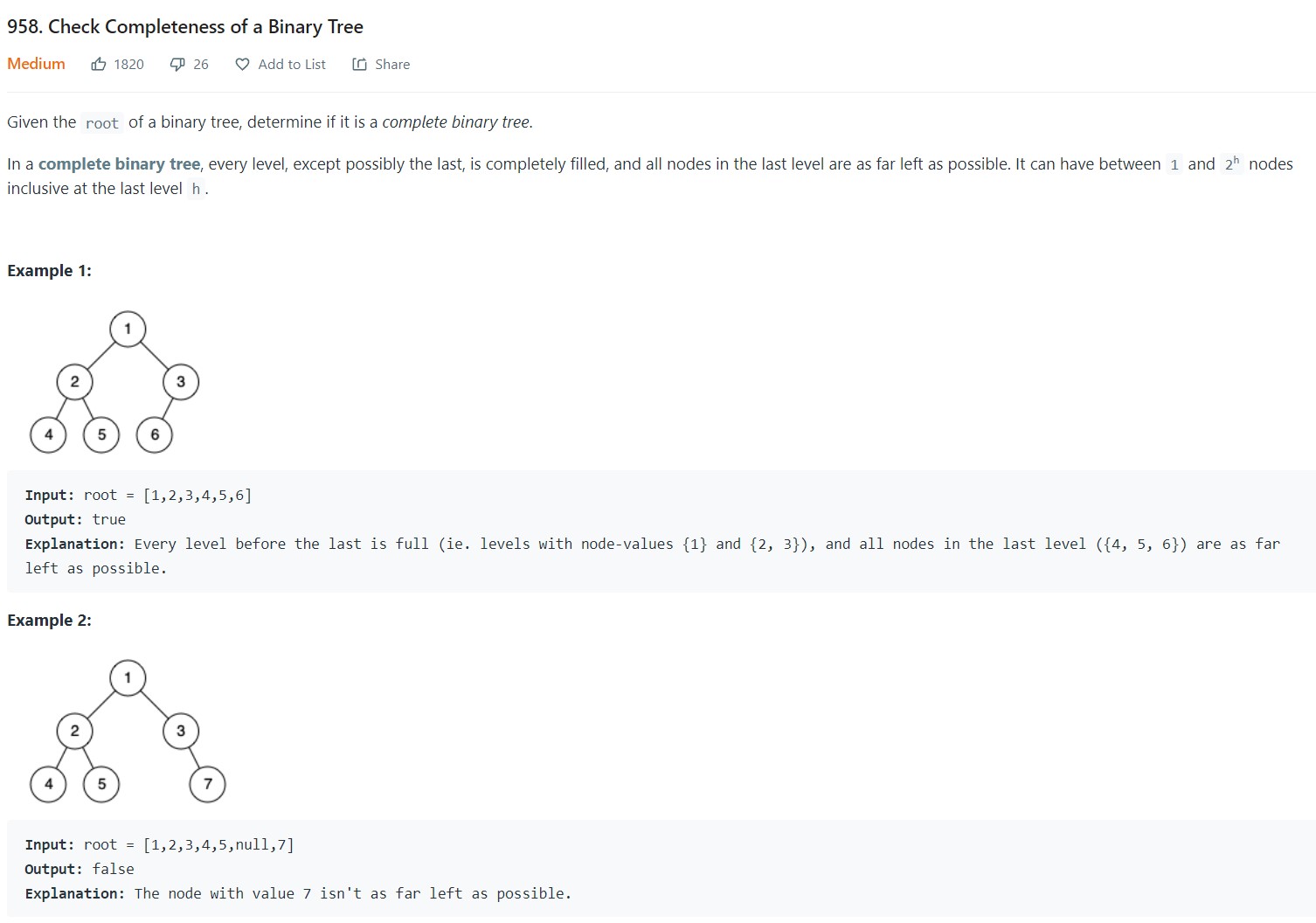
12. Check completeness of a Binary Tree - LC 958 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21def isCompleteTree(self, root: Optional[TreeNode]) -> bool: if root is None: return False expectedid = 1 q = deque([(root, 1)]) while len(q): numnodes = len(q) for _ in range(numnodes): (node, id) = q.popleft() if id == expectedid: expectedid += 1 else: return False if node.left is not None: q.append((node.left, 2*id)) if node.right is not None: q.append((node.right, 2*id + 1)) return True
-
Points to Note
Binary heap has two properties:
-
Structural Property:
- Complete binary tree (except possibly the last one)
- All the nodes in the last level are as far left as possible.
-
Heap Property:
- Priority of every node needs to be less than priority its two children if it is min heap and larger if it is max heap.
-
The above property can be used for this problem.
-
Number the nodes (address or roll number) from 1 onwards from left to right.
-
Thus level order traversal of this binary tree will correspond to the order in which they appear in an array.
-
There is a clean relationship between node and its parent.
- To go to parent: Take the address and divide by two. Instead of following pointers, we can use
the index to reach parent.
- To go down to left child, double the address and
- To get to right child double the address + 1
-
If we do a level order traversal, all the nodes should appear consequtively. If there is any null/gap in the middle, then the tree is not complete binary tree.
-
-
Complexity Analysis
- Time Complexity: \(O(n)\)
- Space Complexity: \(O(n)\) Length of the queue
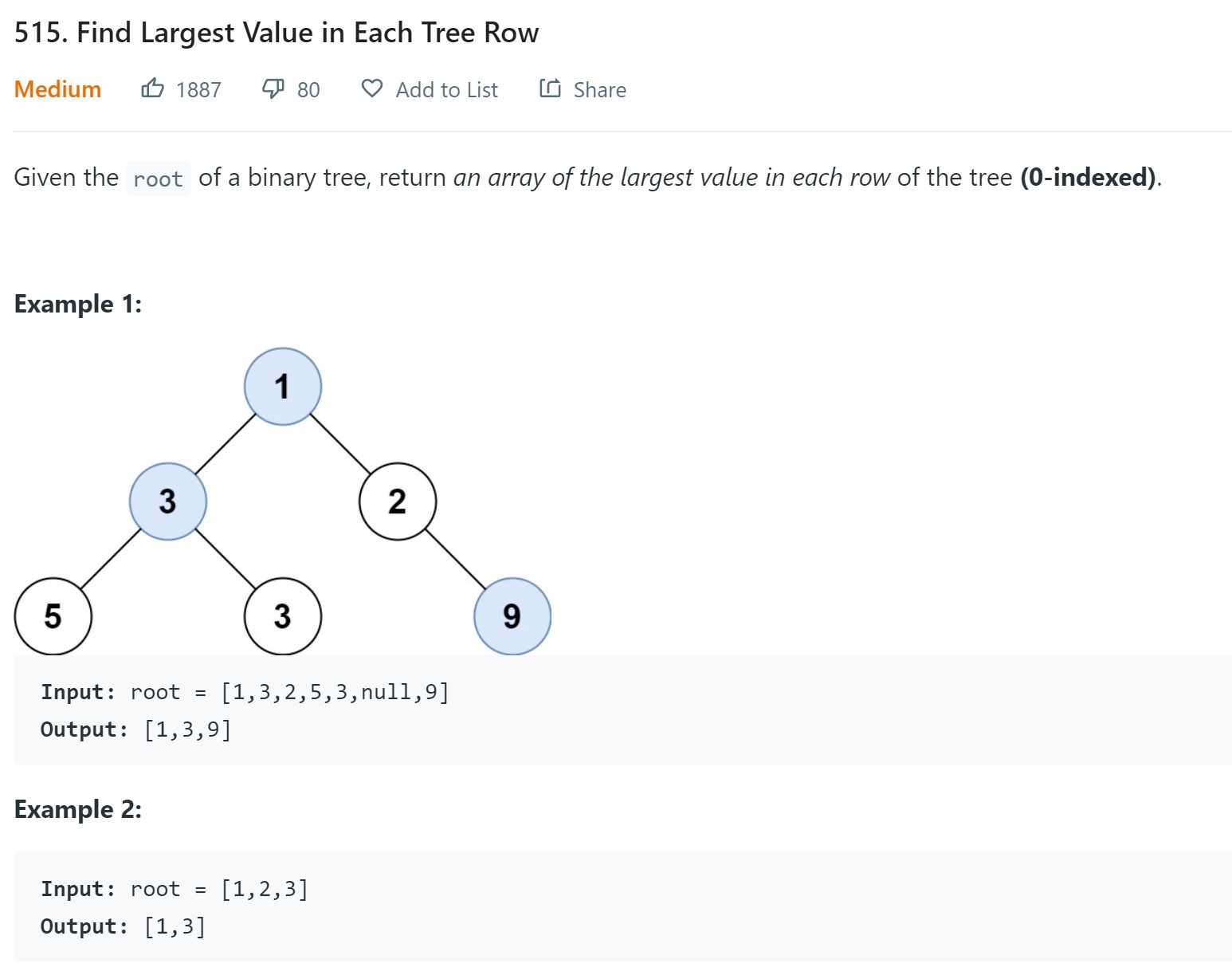
13. Find largest value in each tree row - LC 515 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def largestValues(self, root: Optional[TreeNode]) -> List[int]: if root is None: return [] result = [] q = deque([root]) largest = float(-inf) while len(q): numnodes = len(q) largest = float(-inf) for _ in range(numnodes): node = q.popleft() largest = max(largest, node.val) if node.left is not None: q.append(node.left) if node.right is not None: q.append(node.right) result.append(largest) return result
- Complexity Analysis
-
Coding Mistakes
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18def largestValues(root: Optional[TreeNode]) -> List[int]: if root is None: return [] result = [] q = deque([root]) while len(q): numnodes = len(q) largest = float(-inf) #2022-02-28: This variable should be declared here not outside while loop for _ in range(numnodes): node = q.popleft() largest = max(largest, node.val) if node.left is not None: q.append(node.left) if node.right is not None: q.append(node.right) result.append(largest) return result
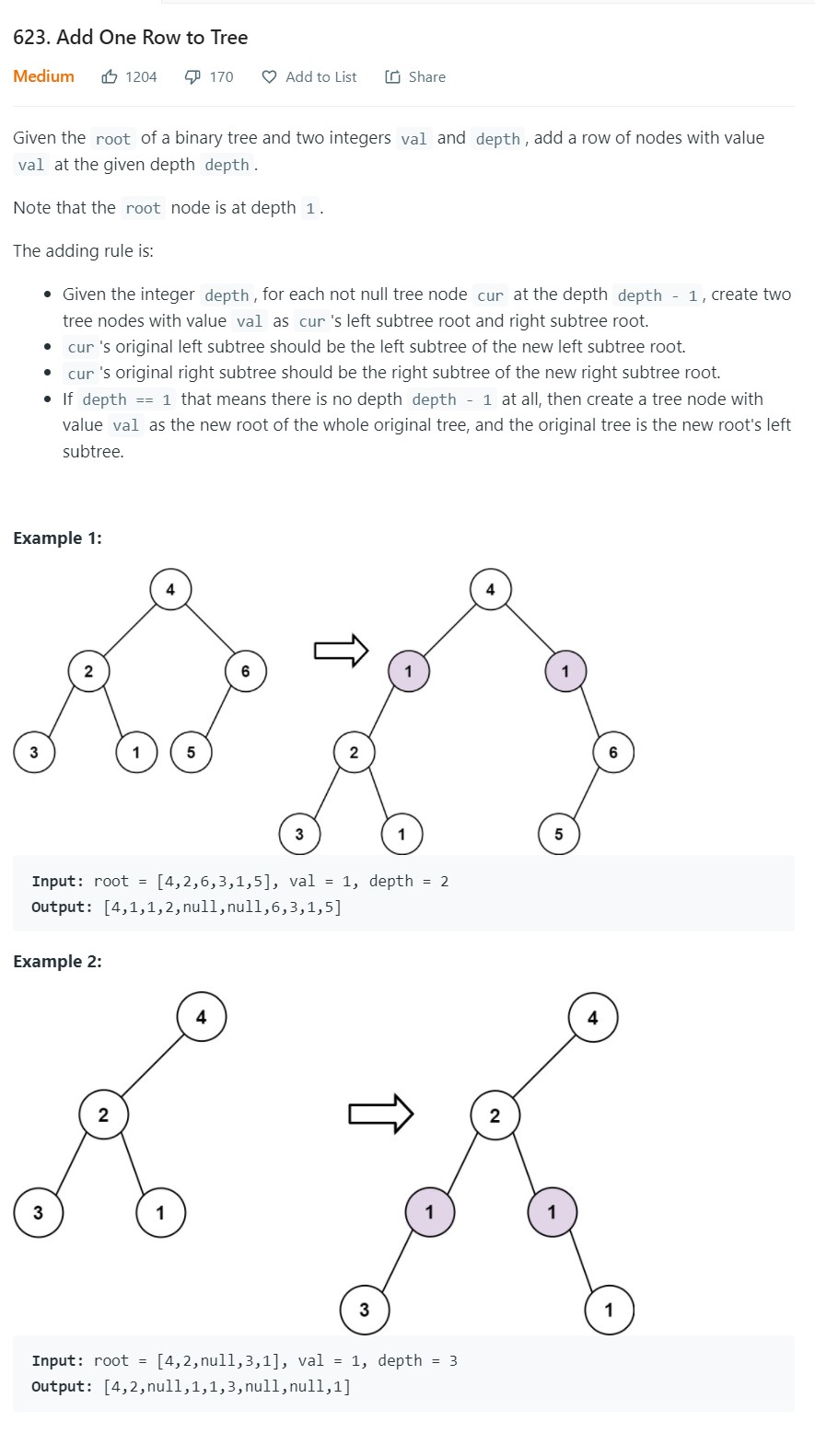
14. Add one row to Tree - LC 623 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def addOneRow(self, root: Optional[TreeNode], val: int, depth: int) -> Optional[TreeNode]: if depth == 1: newnode = TreeNode(val = val) newnode.left = root root = newnode return root q = deque([root]) level = 0 while len(q): numnodes = len(q) level += 1 for _ in range(numnodes): node = q.popleft() if level < depth-1: if node.left is not None: q.append(node.left) if node.right is not None: q.append(node.right) elif level == depth-1: newleft = TreeNode(val) newright = TreeNode(val) newleft.left = node.left newright.right = node.right node.left = newleft node.right = newright return root
- Complexity Analysis
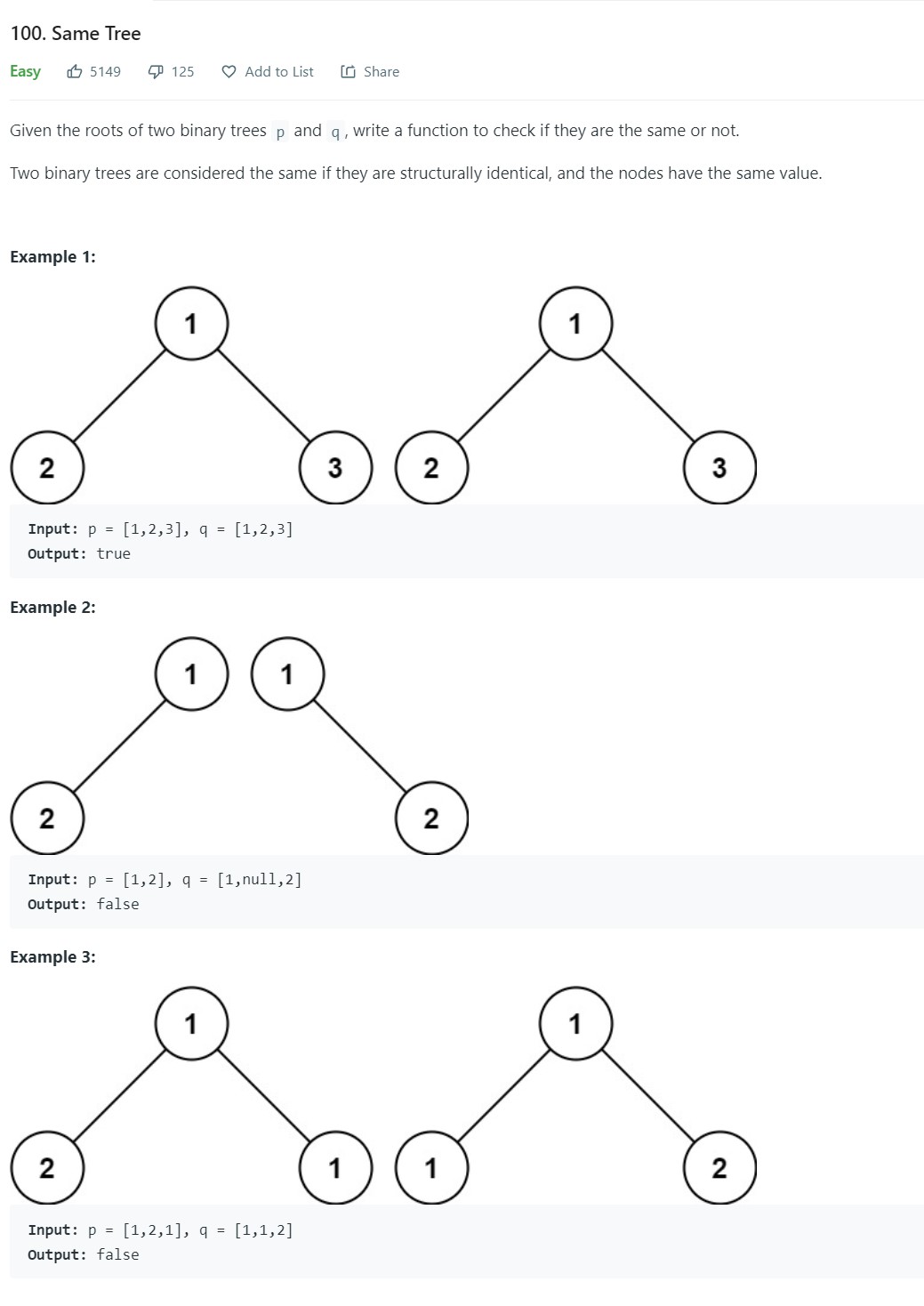
15. Same Tree - LC 100 - Easy
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool: if p is None and q is None: return True if (p is None and q is not None) or (q is None and p is not None): return False q = deque([(p,q)]) while len(q): numnodes = len(q) for _ in range(numnodes): (nodep, nodeq) = q.popleft() if nodep.left is not None and nodeq.left is not None: #Both have left child q.append((nodep.left, nodeq.left)) elif nodep.left is not None or nodeq.left is not None: # One of the child is Null return False if nodep.right is not None and nodeq.right is not None: # Both have right child q.append((nodep.right, nodeq.right)) elif nodep.right is not None or nodeq.right is not None: # One of the right child is Null return False if nodep.val != nodeq.val: return False return True
-
Points to Note:
- If both the roots of the trees are null, return true. If one of them is null, return false
- If both the roots are non-null, then add them to the queue. We have a few conditions:
- Check if both of them are null
- check if one of them is null
- Use two queues if it is useful
- The edge case for single tree is if root is Null. For two trees, atleast one of them is null.
- If both the nodes have no children, then nothing to be done.
-
Complexity Analysis
- Time Complexity = \(O(N)\)
- Space Complexity = \(O(N)\)
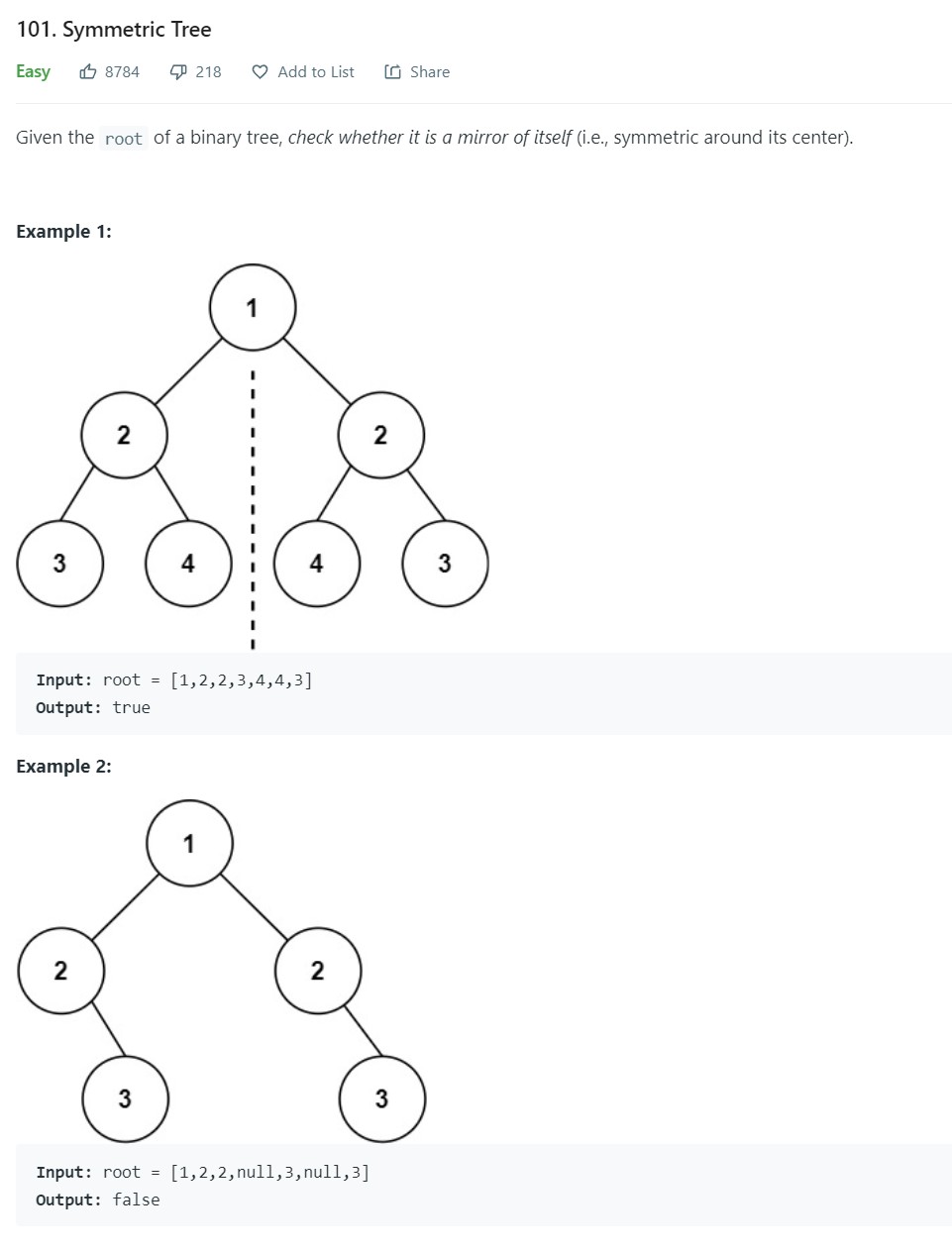
16. Symmetric Tree - LC 101 - Easy
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def isSymmetric(self, root: Optional[TreeNode]) -> bool: if root is None: return True q = deque([(root, root)]) while len(q): numnodes = len(q) for _ in range(numnodes): nodeL, nodeR = q.popleft() if nodeL.left is not None and nodeR.right is not None: q.append((nodeL.left, nodeR.right)) elif nodeL.left is not None or nodeR.right is not None: return False if nodeL.right is not None and nodeR.left is not None: q.append((nodeL.right, nodeR.left)) elif nodeL.right is not None or nodeR.left is not None: return False if nodeL.val != nodeR.val: return False return True
- Complexity Analysis
17. Populating next pointers in each node - LC 116 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29""" # Definition for a Node. class Node: def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None): self.val = val self.left = left self.right = right self.next = next """ class Solution: def connect(self, root: 'Optional[Node]') -> 'Optional[Node]': if root is None: return None q = deque([root]) while len(q): numnodes = len(q) prevnode = None for _ in range(numnodes): node = q.popleft() if node.left is not None: q.append(node.left) if node.right is not None: q.append(node.right) if prevnode is not None: prevnode.next = node prevnode = node return root
- Complexity Analysis
18. Clone a binary Tree (Not an LC problem)
Stack
1. Binary Tree preorder traversal - 144 - Easy
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29#Iterative Solution # Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]: if root is None: return None result = [] stack = [(root, None)] while len(stack): (node, zone) = stack[-1] if zone is None: stack[-1] = (node, 'arrival') result.append(node.val) if node.left is not None: stack.append((node.left, None)) elif zone == 'arrival': stack[-1] = (node, "interim") if node.right is not None: stack.append((node.right, None)) elif zone == 'interim': stack[-1] = ((node, 'departure')) stack.pop() return result
- Complexity Analysis
2. Binary Tree Inorder traversal - 94 - Easy
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]: if root is None: return [] result = [] stack = [(root, None)] while stack: (node, zone) = stack[-1] if zone is None: stack[-1] = (node, 'arrival') if node.left is not None: stack.append((node.left, None)) elif zone == 'arrival': stack[-1] = (node, 'interim') result.append(node.val) if node.right is not None: stack.append((node.right, None)) elif zone == 'interim': stack[-1] = (node, 'departure') stack.pop() return result
- Complexity Analysis
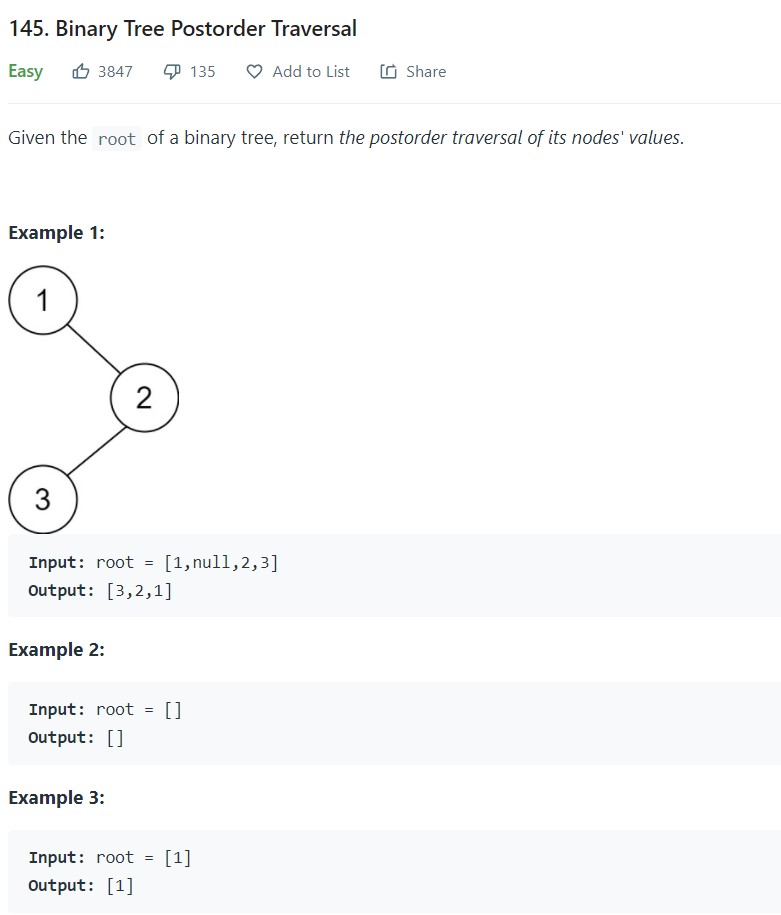
3. Binary Tree Postorder traversal - 145 - Easy
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right #Iterative Solution class Solution: def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]: if root is None: return [] result = [] stack = [(root, None)] while stack: (node, zone) = stack[-1] if zone is None: stack[-1] = (node, 'arrival') if node.left is not None: stack.append((node.left, None)) elif zone == 'arrival': stack[-1] = (node, 'interim') if node.right is not None: stack.append((node.right, None)) elif zone == 'interim': stack[-1] = ((node, 'departure')) result.append(node.val) stack.pop() return result # Recursive Solution: # Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]: result = [] if root is None: return result def dfs(node): if node.left is None and node.right is None: result.append(node.val) return if node.left is not None: dfs(node.left) if node.right is not None: dfs(node.right) result.append(node.val) dfs(root) return result
- Complexity Analysis
Top Down DFS
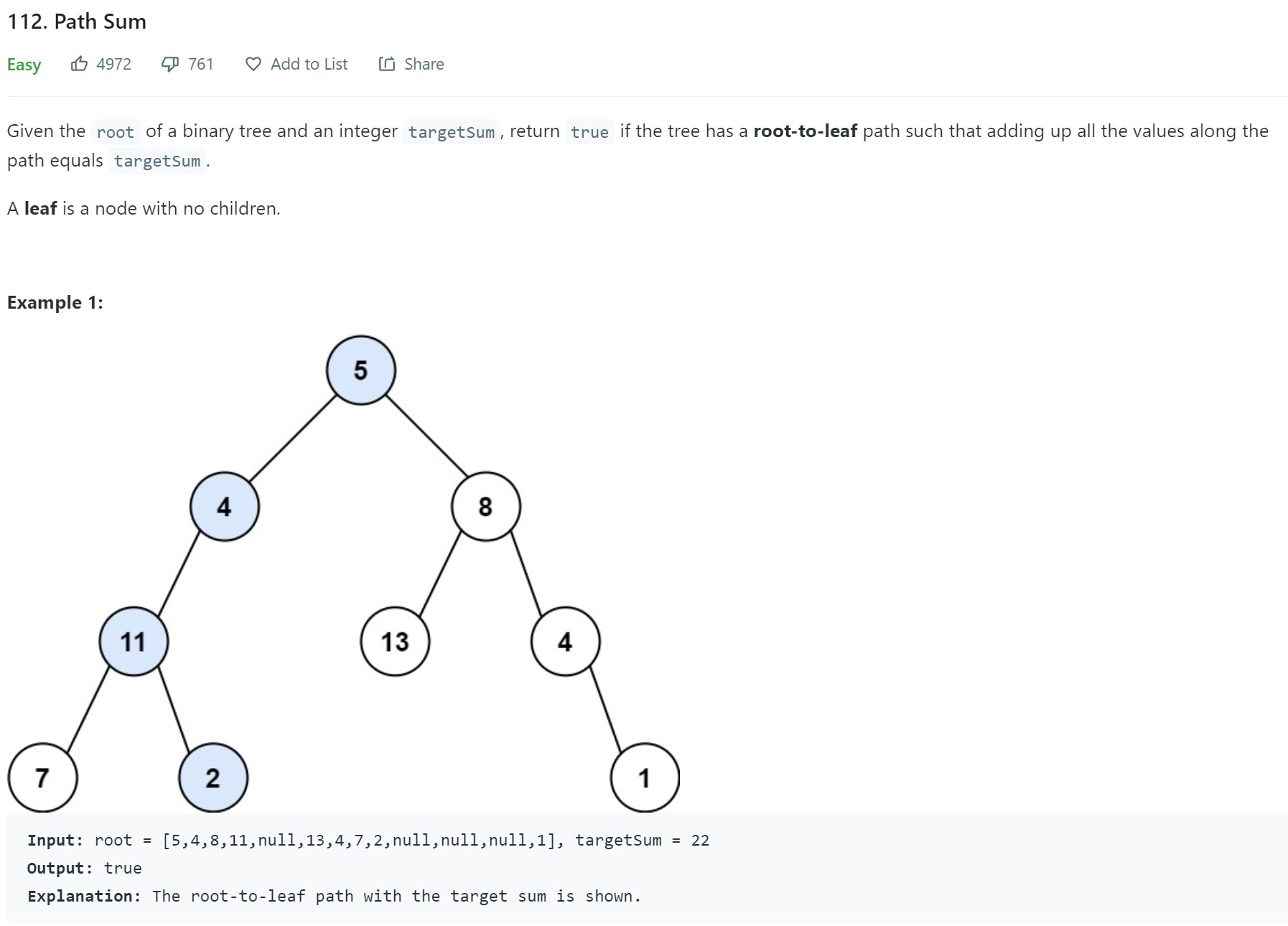
1. Path Sum - LC 112 - Easy
-
Code
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool: if root is None: return False result = [False] def dfs(node, target): if node.left is None and node.right is None: if node.val == target: result[0] = True return if node.left is not None: dfs(node.left, target- node.val) if node.right is not None: dfs(node.right, target-node.val) dfs(root, targetSum) return result[0]
-
Points to Note
- The reason edge case is checked at the parent is because in this case if the sum is 0, and tree is empty, leetcode wants to return false.
-
In Top down DFS, important part is the area (pre order) where the info. is passed to sub ordinates.
-
Using global bag to fill the response from internal stack frame is tricky in python. It should not be a variable but a list[0]. Keep this in mind.
-
Complexity
-
Time complexity: Each worker is doing constant amoutn of work whether internal or leaf node worker. There are at max N nodes so N workers = O(N)
-
The maxisum size of the call stack is equal to the max height of the tree so space complexity is O(N). This is usual of Top down DFS.
-
-
Coding Mistakes
2022-02-28:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16class Solution: def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool: if root is None: return False result = [False] def dfs(node, target): if node.left is None and node.right is None: if node.val == target: result[0] = True return if node.left is not None: dfs(node.left, target- node.val) if node.right is not None: dfs(node.right, target-node.val) dfs(root, targetSum) return result[0]
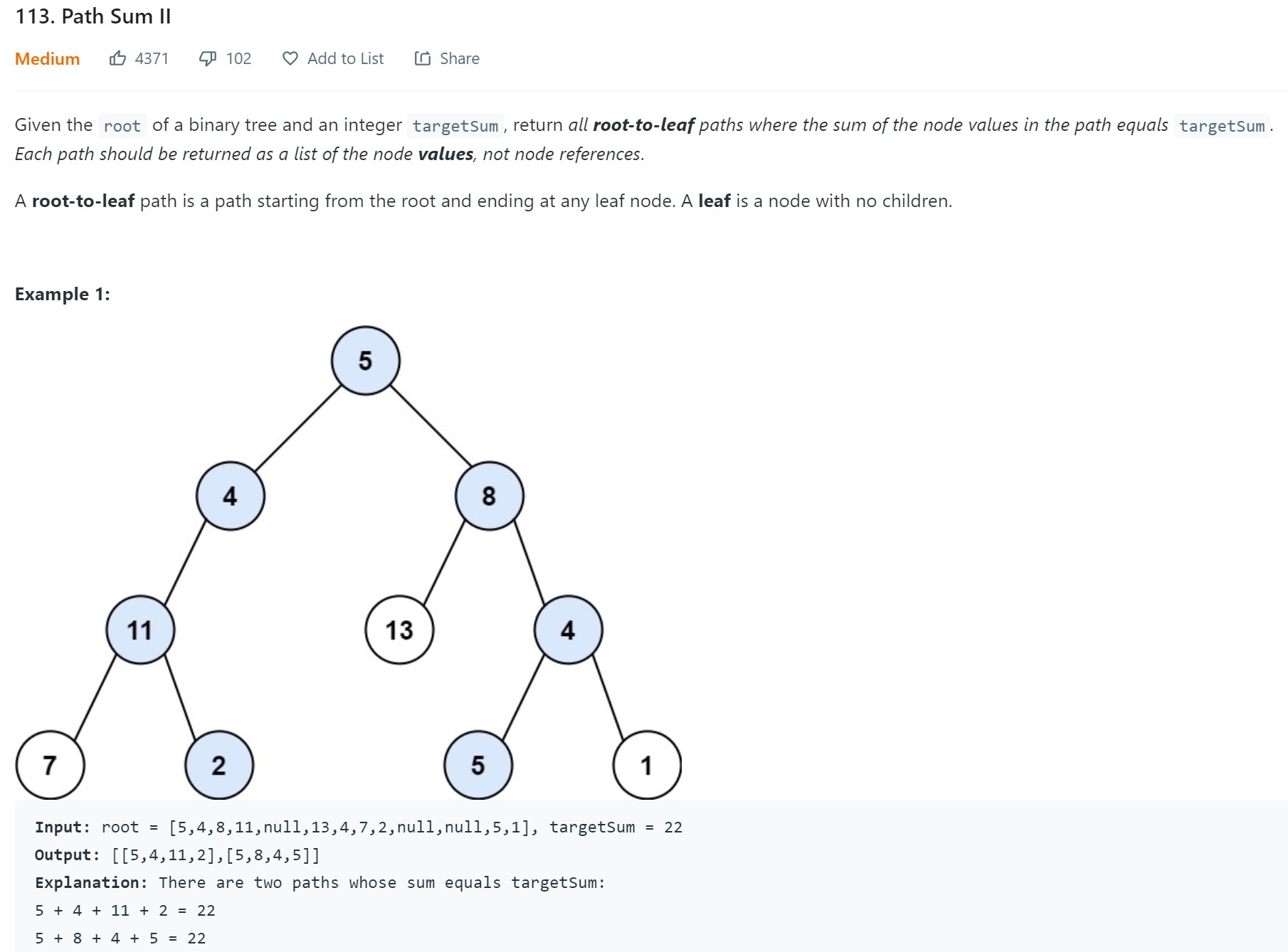
2. Path Sum II - LC 113 - Medium
-
Code
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]: if root is None: return [] result = [] def dfs(node, target, slate): if node.left is None and node.right is None: if node.val == target: slate.append(node.val) result.append(slate[:]) slate.pop() return else: if node.left is not None: slate.append(node.val) dfs(node.left, target - node.val, slate) slate.pop() if node.right is not None: slate.append(node.val) dfs(node.right, target - node.val, slate) slate.pop() dfs(root, targetSum, []) return result
-
Points to Note:
- Remember to pop off the slate once it is appended…(even for the leaf node). The output may have duplicate root values if slate is not popped in the base case.
-
Complexity:
- Time complexity: In this case, there is additional effort of copying the slate to global box. In a complete balance binary tree, there are roughly n/2 workers at leaf level. The worst case could be that each and every path is adding up to the target sum. The length of the slate could be log N in this case and since there are n/2 workers it could be n/2 log N or NlogN. - Space Complexity: Every single path could be added to the global result and there are n/2 paths and each path could be of log N long. So the space complexity also is NlogN. - Here is it not hte call stack but copying the data to global box is the bottleneck.
Bottom Up DFS
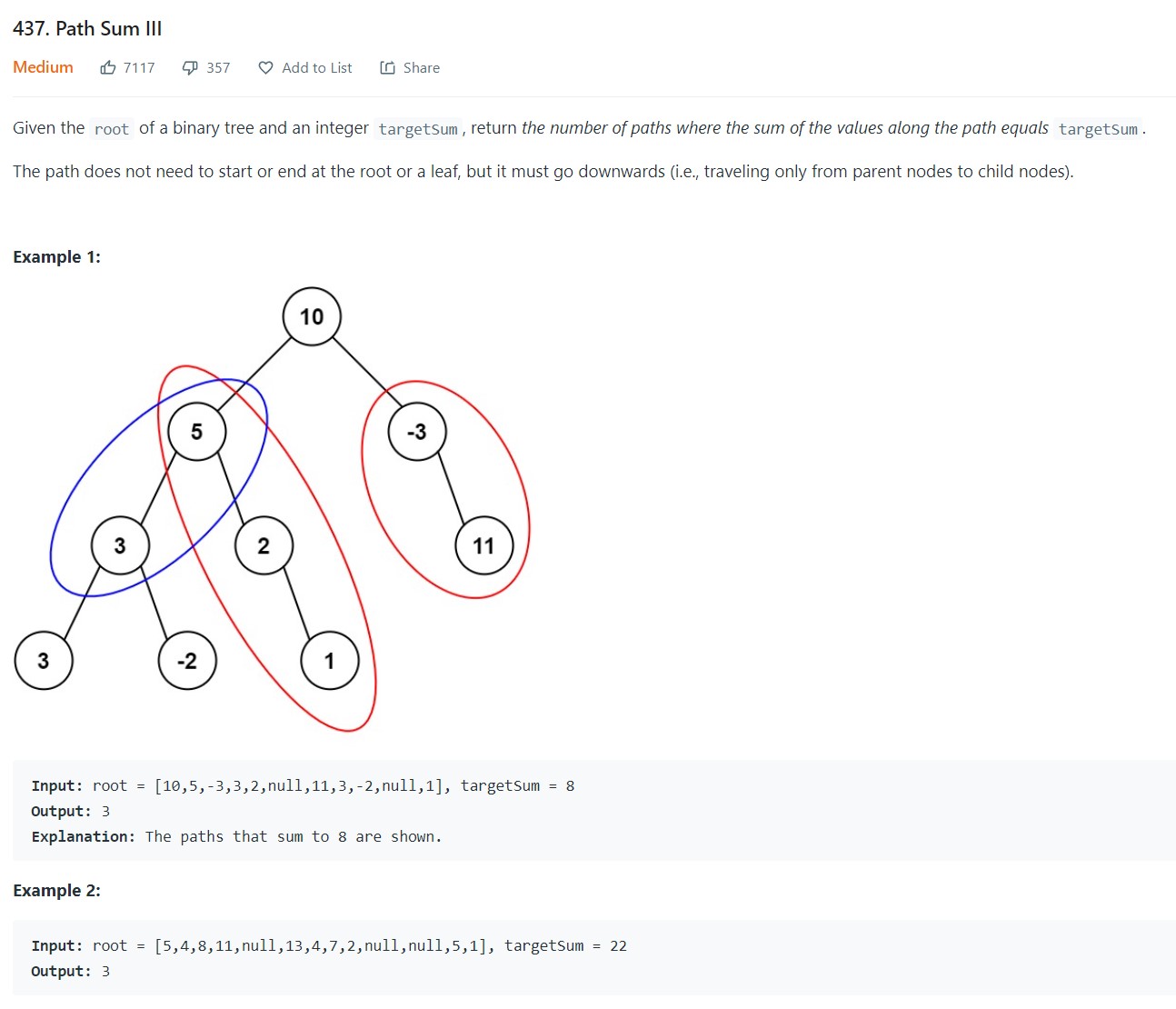
3. Path Sum III - LC 437 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int: if root is None: return 0 globalcount = [0] def dfs(node, target, slate): slate.append(node.val) #Check every suffix sum to see how many add up to the target suffixsum = 0 for i in range(len(slate)-1, -1, -1): suffixsum += slate[i] if suffixsum == target: globalcount[0] += 1 #Base Case: if node.left is None and node.right is None: pass if node.left is not None: dfs(node.left, target, slate) if node.right is not None: dfs(node.right, target, slate) slate.pop() dfs(root, targetSum, []) return globalcount[0]
4. Invert Binary Tree - LC 226 - Easy
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]: # DFS Approach ''' if root is None: return None right = self.invertTree(root.right) left = self.invertTree(root.left) root.right = left root.left = right return root ''' # BFS Approach if root is None: return None q = deque([root]) while len(q): node = q.popleft() node.left, node.right = node.right, node.left if node.left is not None: q.append(node.left) if node.right is not None: q.append(node.right) return root
5. Binary Tree Longest Consecutive Sequence - LC 298 - Medium
Video: Tree Series 2 - 2:10:32 hrs
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27class Solution: def longestConsecutive(self, root: Optional[TreeNode]) -> int: if root is None: return 0 globalmax = [0] def dfs(node, pval, lengthsofar): # Common to base and leaf nodes: if node.val == pval + 1: lengthsofar += 1 else: lengthsofar = 1 if lengthsofar > globalmax[0]: globalmax[0] = lengthsofar #Base Case: if node.left is None and node.right is None: pass if node.left is not None: dfs(node.left, node.val, lengthsofar) if node.right is not None: dfs(node.right, node.val, lengthsofar) dfs(root, root.val, 0) return globalmax[0]
-
Points to Note
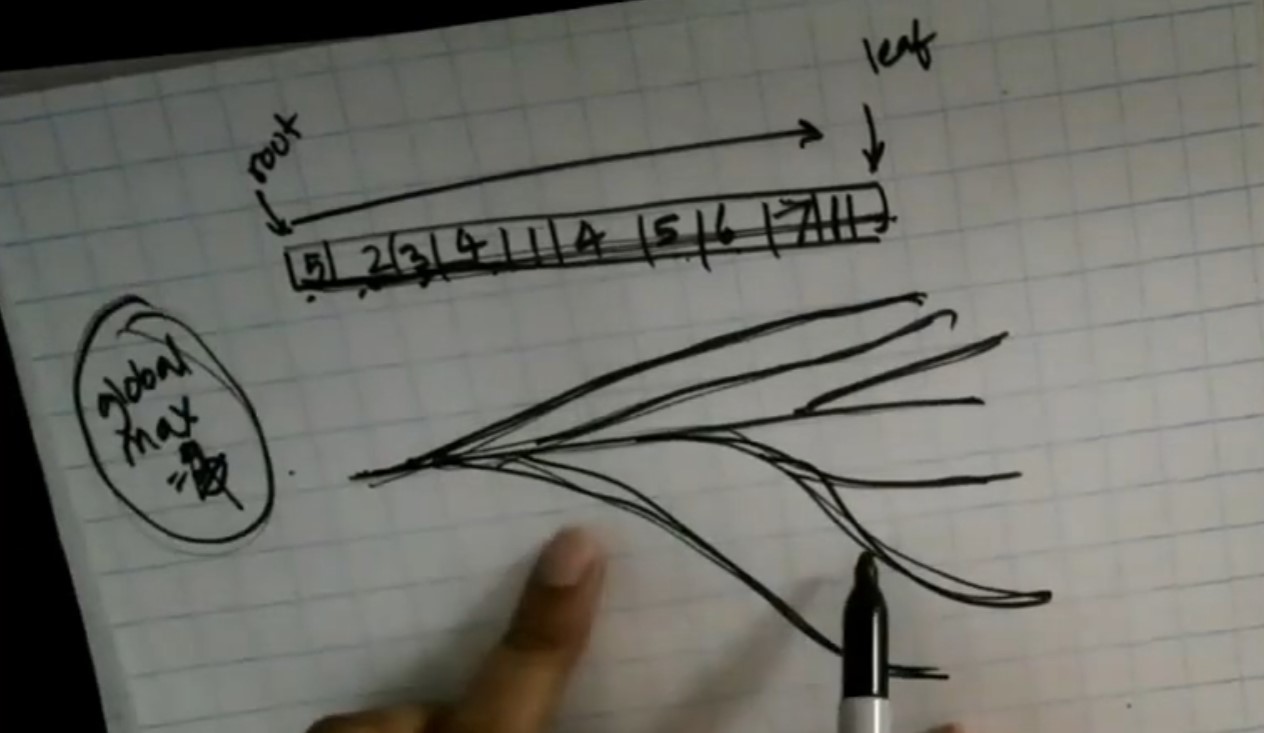
- One single path..need not start from root nor end at leaf level. The nodes should have consequtive values.
- Only ascending order.
- Single scan from left to right. Keep a consequtive sequence that is current. Update the global max if the current sequence is higher than global max
- Two things to be done:
- Extending current consequtive sequence
- Keep a global max.
- Since we are going different paths, use depth first search.
- In each path, it is effectively like searching an array, going from left to right
- At any point, parent has to pass the current sequence length.
- We also need to know that we are extending parent’s value by 1.
-
Complexity Analysis
- Time Complexity: \(O(N)\)
- Space Complexity: \(O(N)\)
6. Binary Tree Vertical Order Traversal - LC 314 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def verticalOrder(self, root: Optional[TreeNode]) -> List[List[int]]: if root is None: return [] nlist = [] plist = [] zlist = [[]] q = deque([(root, 0)]) while len(q): (node, x) = q.popleft() if x < 0: if len(nlist) < abs(x): nlist.append([]) nlist[abs(x) - 1].append(node.val) elif x > 0: if len(plist) < x: plist.append([]) plist[x-1].append(node.val) else: zlist[0].append(node.val) if node.left is not None: q.append((node.left, x-1)) if node.right is not None: q.append((node.right, x+1)) nlist.reverse() nlist.extend(zlist) nlist.extend(plist) return nlist
- Points to Note
7. Find Bottom Left Tree value - LC 513 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def findBottomLeftValue(self, root: Optional[TreeNode]) -> int: # BFS Approach q = deque([root]) while len(q): numnodes = len(q) firstvalue = None for _ in range(numnodes): node = q.popleft() if firstvalue is None: firstvalue = node.val if node.left is not None: q.append(node.left) if node.right is not None: q.append(node.right) return firstvalue # DFS Approach leftmost = [] def dfs(node, parentdepth): mydepth = parentdepth + 1 if mydepth > len(leftmost): leftmost.append(node.val) if node.left is None and node.right is None: pass if node.left is not None: dfs(node.left, mydepth) if node.right is not None: dfs(node.right, mydepth) dfs(root, 0) return leftmost[-1]
- Complexity Analysis
8. Vertical Order Traversal of a Binary Tree - LC 987 - Hard
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def verticalTraversal(self, root: Optional[TreeNode]) -> List[List[int]]: result = {} if root is None: return [] def dfs(node, x, y): if x not in result: result[x] = {} if y not in result[x]: result[x][y] = [node.val] else: result[x][y].append(node.val) if node.left is not None: dfs(node.left, x-1, y+1) if node.right is not None: dfs(node.right, x+1, y+1) dfs(root, 0, 0) output = [] for x in sorted(result.keys()): temp = [] for y in sorted(result[x].keys()): temp.extend(sorted(result[x][y])) output.append(temp) return output
- Complexity Analysis
9. Boundary of a Binary Tree - LC 545 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def boundaryOfBinaryTree(self, root: Optional[TreeNode]) -> List[int]: if root is None: return [] if root.left is None and root.right is None: return [root.val] leftboundary = [root.val] if root.left is not None: cur = root.left while cur is not None: leftboundary.append(cur.val) if cur.left is not None: cur = cur.left else: cur = cur.right leftboundary.pop() rightboundary = [] if root.right is not None: cur = root.right while cur is not None: rightboundary.append(cur.val) if cur.right is not None: cur = cur.right else: cur = cur.left rightboundary.pop() rightboundary.reverse() leaves = [] def dfs(node): if node.left is None and node.right is None: leaves.append(node.val) if node.left is not None: dfs(node.left) if node.right is not None: dfs(node.right) dfs(root) return leftboundary + leaves + rightboundary
- Complexity Analysis
10. Binary Tree Upside Down - LC 156 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def upsideDownBinaryTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]: if root is None: return None globalroot = [None] def dfs(node, parent, rightsibling): oldleft = node.left oldright = node.right node.right = parent node.left = rightsibling if oldleft is None and oldright is None: globalroot[0] = node if oldleft is not None: dfs(oldleft, node, oldright) dfs(root, None, None) return globalroot[0]
- Complexity Analysis
11. Populating Next Right Pointers in each Node II - LC 117 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def isUnivalTree(self, root: Optional[TreeNode]) -> bool: if root is None: return False q = deque([root]) while len(q): node = q.popleft() if node.left is not None and node.right is not None: if node.left.val != node.right.val: return False if node.left.val != node.val: return False if node.left is not None: q.append(node.left) if node.left.val != node.val: return False if node.right is not None: q.append(node.right) if node.right.val != node.val: return False return True
- Complexity Analysis
12. Merge Two Binary Trees - 617 - Easy
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]: if root1 is None: return root2 if root2 is None: return root1 def dfs(node1, node2): #First node is the base. Second node will merge with it node1.val += node2.val if node1.left is not None: if node2.left is not None: dfs(node1.left, node2.left) #Nothing to do if second node left is Null else: node1.left = node2.left #Do the same for right tree if node1.right is not None: if node2.right is not None: dfs(node1.right, node2.right) else: node1.right = node2.right dfs(root1, root2) return root1
- Complexity Analysis
Bottom Up DFS
1. Count Univalue Subtrees - LC 250 - Medium
-
Code
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def countUnivalSubtrees(self, root: Optional[TreeNode]) -> int: result = [0] if root is None: return 0 def dfs(node): am_i_unival = True #Base Case if node.left is None and node.right is None: result[0] += 1 return True #Recursive Case if node.left is not None: is_left_unival = dfs(node.left) if not is_left_unival or (node.val != node.left.val): am_i_unival = False if node.right is not None: is_right_unival = dfs(node.right) if not is_right_unival or (node.val != node.right.val): am_i_unival = False if am_i_unival == True: result[0] += 1 return am_i_unival dfs(root) return result[0]
-
Points to Note:
-
This is bottom dfs problem. There is no useful info coming from the parent node.
-
Each child node has to find out if its left and right subtree are unival and if so, compare its value to the values of the left and right subtree to confirm if the node is unival. Then return it to the parent.
-
This means the sub function has explicit return to the parent.
-
In addition, each node has to update the global box with the incremented count of the univals.
-
-
Complexity:
- Time complexity: In this case, there is additional effort of copying the slate to global box. In a complete balance binary tree, there are roughly n/2 workers at leaf level. The worst case could be that each and every path is adding up to the target sum. The length of the slate could be log N in this case and since there are n/2 workers it could be n/2 log N or NlogN. - Space Complexity: Every single path could be added to the global result and there are n/2 paths and each path could be of log N long. So the space complexity also is NlogN. - Here it is not the call stack but copying the data to global box is the bottleneck.
2. Binary Tree Maximum Path Sum - LC 124 - Hard
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def maxPathSum(self, root: Optional[TreeNode]) -> int: globalmax = [float("-inf")] def dfs(node): mymaxpathsum = node.val mymaxvpathsum = node.val if node.left is None and node.right is None: pass if node.left is not None: leftmax = dfs(node.left) mymaxpathsum = mymaxvpathsum = max(mymaxpathsum, mymaxpathsum + leftmax) if node.right is not None: rightmax = dfs(node.right) mymaxpathsum = max(mymaxpathsum, node.val + rightmax) mymaxvpathsum = max(mymaxvpathsum, node.val + rightmax, mymaxvpathsum + rightmax) if globalmax[0] < mymaxvpathsum: globalmax[0] = mymaxvpathsum return mymaxpathsum dfs(root) return globalmax[0]
- Complexity Analysis
3. Diameter of Binary Tree - LC 543 - Easy
-
Code
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int: result = [0] #global box def dfs(node): myheight,lh,rh = 0,0,0 # Base Case (we are at leaf node) if node.left is None and node.right is None: return 0 #recursive case if node.left is not None: lh = dfs(node.left) myheight += lh + 1 if node.right is not None: rh = dfs(node.right) myheight += rh + 1 result[0] = max(result[0], myheight) # add value to global box return max(lh, rh) + 1 # return max to parent node dfs(root) return result[0]
-
Points to Note:
-
Shape of the diameter appears as inverted V shape. Here the manager cannot go on vacation after delegating the work to the subordinate. This means it cannot be top down dfs. So we have to use bottom up dfs.
-
Purely vertical path can be addressed using top down dfs but the paths that have inverted v shape requires different approach than top down dfs.
-
Can we distribute this problem to each node? as a local problem? i.e Each node finds the longest V path thru itself.
-
The global solutoin should be maximum of all local solutions.
-
Each node has to do two things to solve this problem
-
Compute the height at the node level (own height) and pass it to parent node
-
Calculate the local solution for left tree height and right tree height.
-
Code for the above two things can interleave so the safer approach is to write the code for the first subsolution and then interleave the code for the second subsolution.
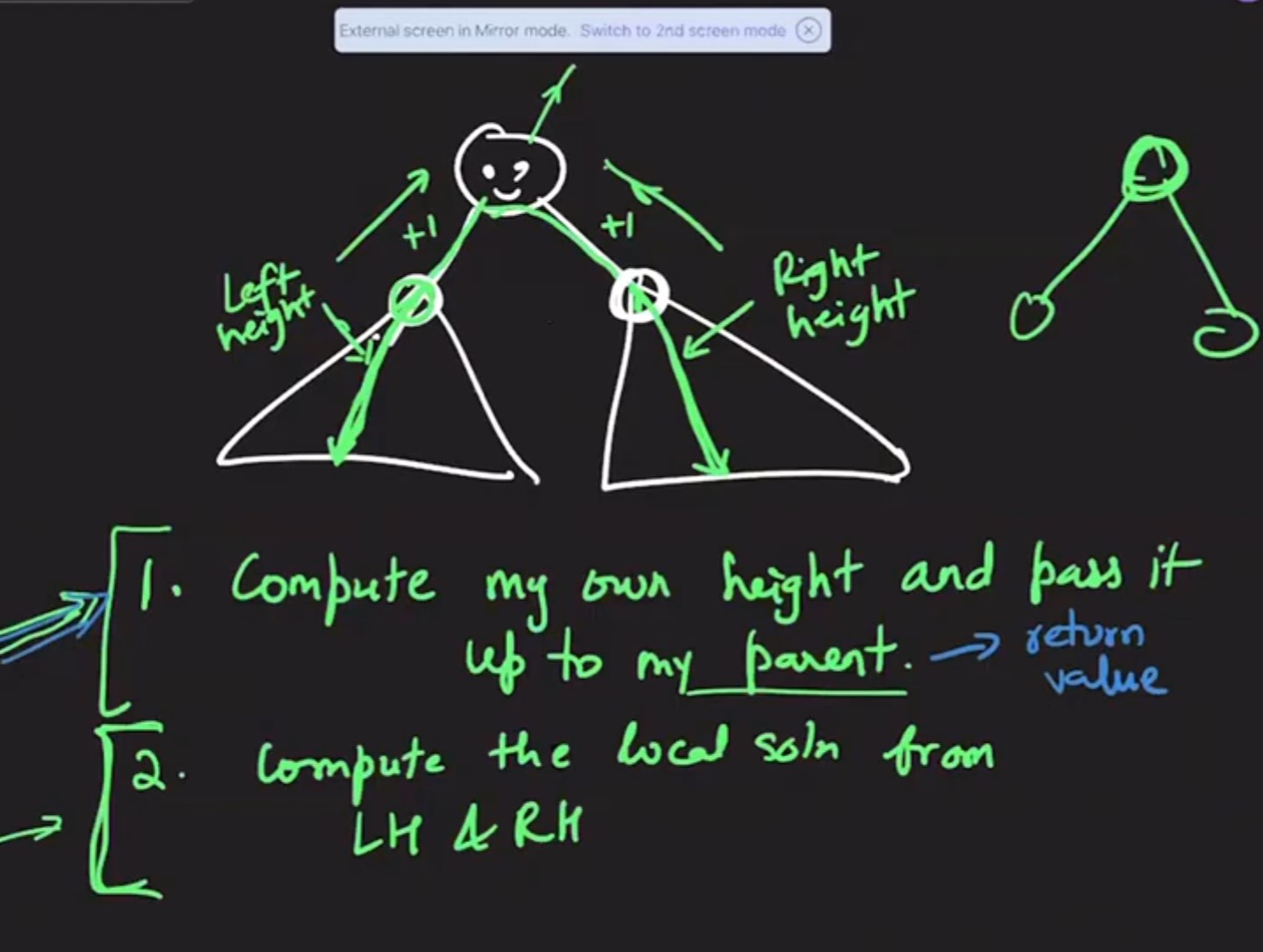
-
Do not assume both left side and right side tree exits. So we should not add 1 to maximum value for obtoh sides. Check if hte tree exits and then add 1.
-
Remember the Edge Cases:
- Initialize lh and rh to 0
- return result[0] and not result
- check the max and add 1 instead of lh+rh+2 because both trees need not exist
-
-
-
Complexity:
- Time complexity: In this case, there is additional effort of copying the slate to global box. In a complete balance binary tree, there are roughly n/2 workers at leaf level. The worst case could be that each and every path is adding up to the target sum. The length of the slate could be log N in this case and since there are n/2 workers it could be n/2 log N or NlogN. - Space Complexity: Every single path could be added to the global result and there are n/2 paths and each path could be of log N long. So the space complexity also is NlogN. - Here is it not hte call stack but copying the data to global box is the bottleneck.
-
Coding Mistakes
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35""" For your reference: class BinaryTreeNode: def __init__(self, value): self.value = value self.left = None self.right = None """ def binary_tree_diameter(root): """ Args: root(BinaryTreeNode_int32) Returns: int32 """ # Write your code here. if root is None: return 0 diameter = [0] def dfs(node): if node.left is None and node.right is None: return 0 lh, rh = 0,0 #2022-03-04, unpack error as RHS had just one zero if node.left is not None: lh = dfs(node.left) + 1 if node.right is not None: rh = dfs(node.right) + 1 diameter[0] = max(diameter[0], lh+rh) return max(lh,rh) #2022-03-04: I did lh+rh for max function instead of ',' #2022-03-04: I also did max(lh + rh) + 1 which was not needed dfs(root) return diameter[0]
4. Lowest Common Ancestor of a binary tree - LC 236 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34# Definition for a binary tree node. # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode': LCA = [None] def dfs(node, p, q): pfound, qfound = 0, 0 if node is p: pfound = True elif node is q: qfound = True if node.left is None and node.right is None: pass if node.left is not None: (pf, qf) = dfs(node.left, p, q) pfound = pfound or pf qfound = qfound or qf if node.right is not None: (pf, qf) = dfs(node.right, p, q) pfound = pfound or pf qfound = qfound or qf if pfound and qfound and LCA[0] is None: LCA[0] = node return (pfound, qfound) dfs(root, p, q) return LCA[0]
-
Points to Note:
- LCA could be one of the nodes if it is ancestor of the other
- We cannot solve this using BFS or top down DFS as we need info multiple level down. SO this is bottom up dfs.
- With the cousin’s problem, all we needed was to see if the previous level or parents belonged to same level. Here we need to peek down multiple levels.
- What info. do I need from my child? If P exists or Q exists in its subtree? This info. helps me to decide if I am common ancestor for P and Q. This become my own return values to my parent.
- We need to find the lowest ancestor. The very first time both of the boolean are returned true, it is the lowest ancestor.
5. Longest Unival Path - LC 687 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def isUnivalTree(self, root: Optional[TreeNode]) -> bool: if root is None: return False q = deque([root]) while len(q): node = q.popleft() if node.left is not None and node.right is not None: if node.left.val != node.right.val: return False if node.left.val != node.val: return False if node.left is not None: q.append(node.left) if node.left.val != node.val: return False if node.right is not None: q.append(node.right) if node.right.val != node.val: return False return True
- Complexity Analysis
6. Balanced Binary Tree - LC 110 - Easy
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def isBalanced(self, root: Optional[TreeNode]) -> bool: balanced = [True] if root is None: return True def dfs(node): myheight = 0 leftht = rightht= 0 if node.left is not None: leftht = 1 + dfs(node.left) if node.right is not None: rightht = 1 + dfs(node.right) myheight = max(leftht, rightht) if abs(leftht - rightht) > 1: balanced[0] = False return myheight dfs(root) return balanced[0]
-
Points to Note
7. Binary Tree Tilt - 563 - Easy
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def findTilt(self, root: Optional[TreeNode]) -> int: if root is None: return 0 globaltilt = [0] def dfs(node): if node.left is None and node.right is None: return node.val leftsum, rightsum = 0,0 if node.left is not None: leftsum = dfs(node.left) if node.right is not None: rightsum = dfs(node.right) mysum = node.val + leftsum + rightsum mytilt = abs(leftsum - rightsum) globaltilt[0] += mytilt return mysum dfs(root) return globaltilt[0]
- Complexity Analysis
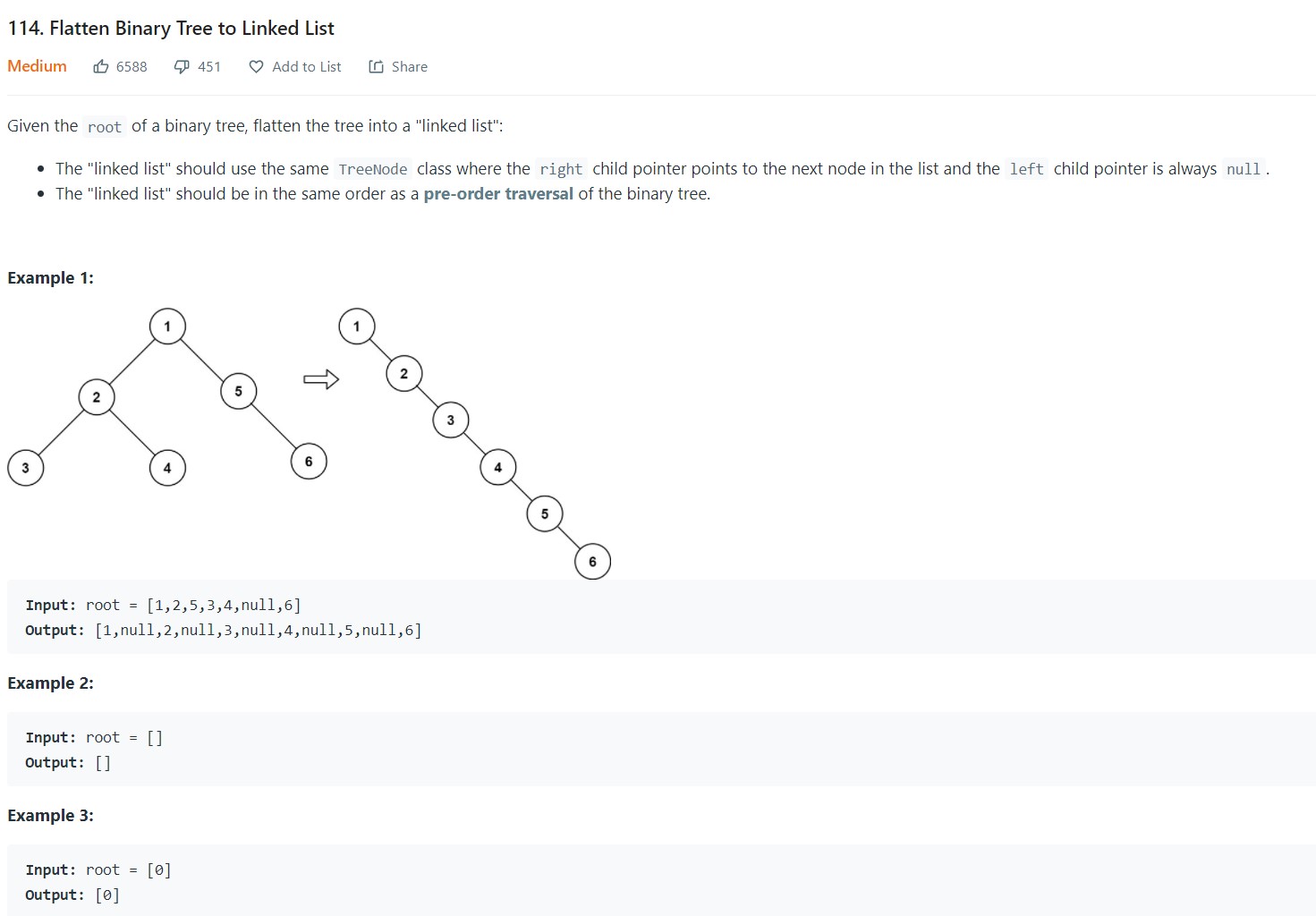
8. Flatten Binary tree to a linked list - 114 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def flatten(self, root: Optional[TreeNode]) -> None: """ Do not return anything, modify root in-place instead. """ if root is None: return None sentinel = TreeNode() #Local problem: Connect each node's preorder predecessor to it. def dfs(node, pred): #Preorder predecessor needs to be updated here before the recursive call pred.left = node pred = node #Base Case, Leaf Node: if node.left is None and node.right is None: return pred #Recursive Case: Internal Node if node.left is not None: pred = dfs(node.left, pred) if node.right is not None: pred = dfs(node.right, pred) return pred dfs(root, sentinel) head = sentinel.left #Now Switch all left pointers to become right pointers cur = head while cur: cur.right = cur.left cur.left = None cur = cur.right return head
- Complexity Analysis
Tree Construction
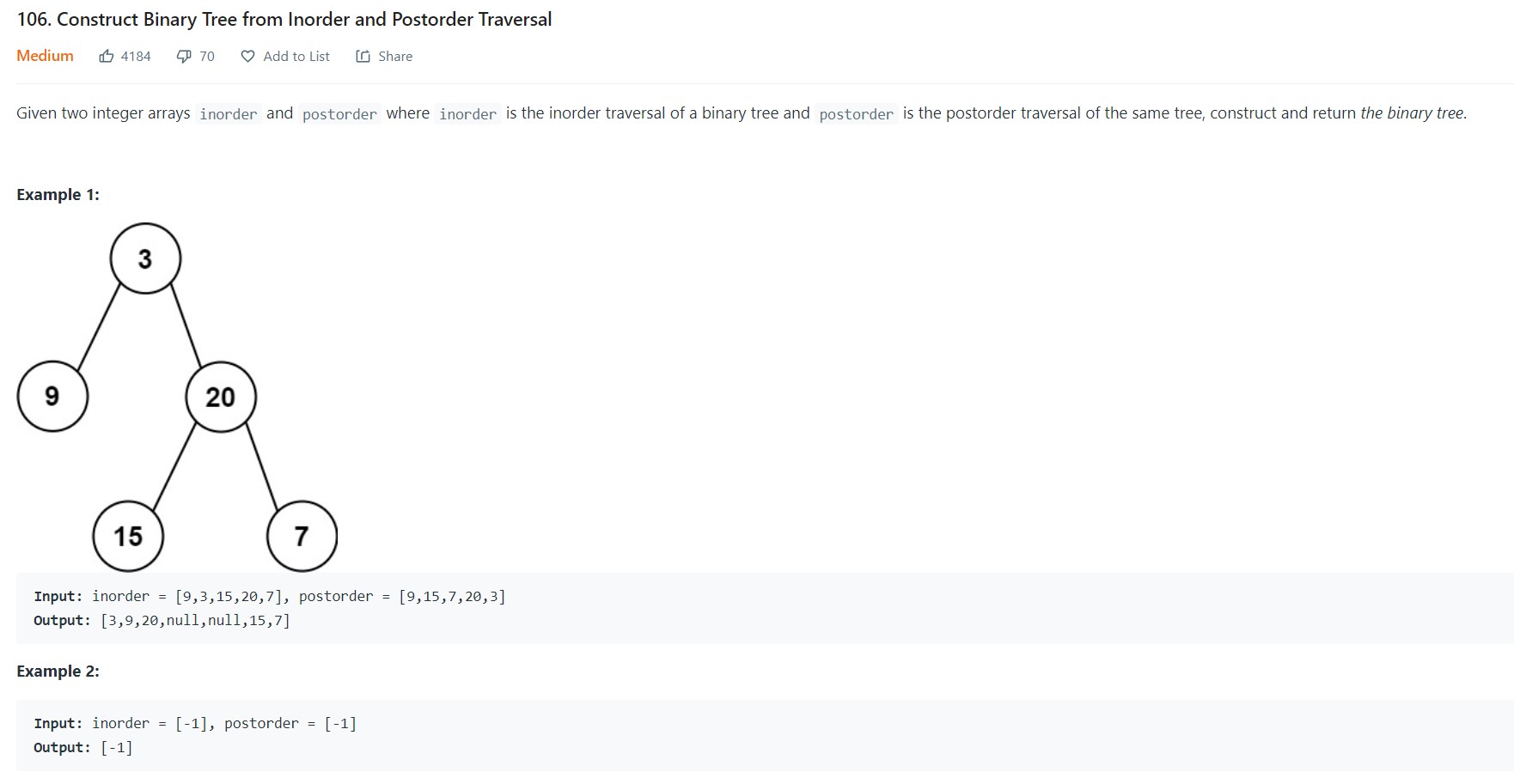
1. Construct Binary Tree from Inorder and Postorder traversal - 106 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def isUnivalTree(self, root: Optional[TreeNode]) -> bool: if root is None: return False q = deque([root]) while len(q): node = q.popleft() if node.left is not None and node.right is not None: if node.left.val != node.right.val: return False if node.left.val != node.val: return False if node.left is not None: q.append(node.left) if node.left.val != node.val: return False if node.right is not None: q.append(node.right) if node.right.val != node.val: return False return True
- Complexity Analysis
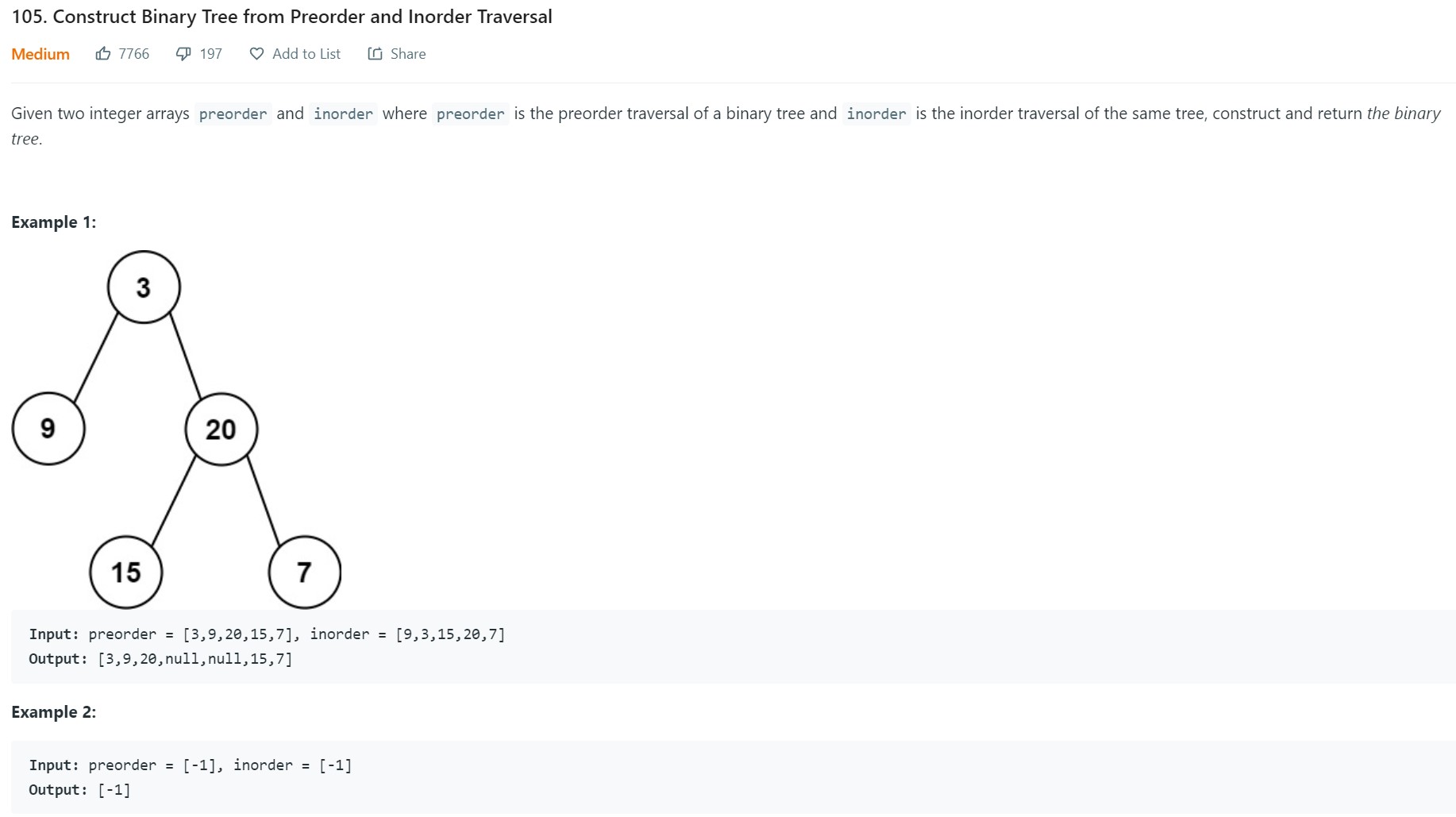
2. Construct binary tree from pre order and in order traversal - LC 105 - Medium
-
Code
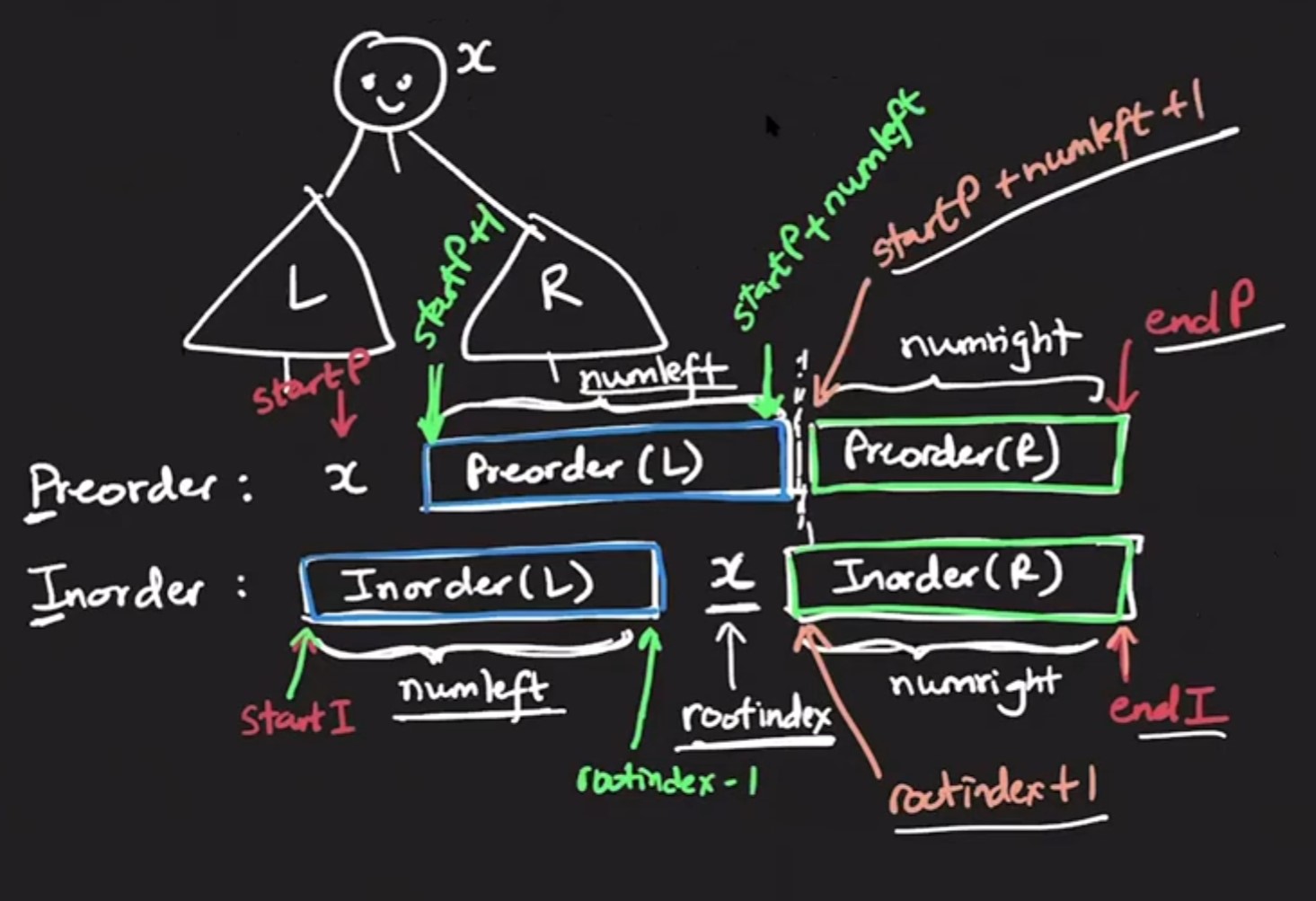
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]: ino_map = {} for i in range(len(inorder)): ino_map[inorder[i]] = i def helper(A1, start1, end1, A2, start2, end2): #return the subtree root of the binary tree constructed from the preorder subarray #A1[start1..end1] and inorder subarray A2[start2..end2] #Base Case if start1 > end1: return None if start1 == end1: return TreeNode(A1[start1]) #At this point we know that preorder subarray is more than 1. #Recursive Case #The first value in the preorder subarray is the root of the subtree rootval = A1[start1] #Find the index of this value in the inorder subarray. #It is guaranteed to be present in the inorder subarray rootindex = ino_map[rootval] #Everything to its left is the left subtree and everything to its right is the right subtree numleft = rootindex - start2 numright = end2 - rootindex subtreeroot = TreeNode(rootval) subtreeroot.left = helper(A1, start1+1, start1+numleft, A2, start2, rootindex-1) subtreeroot.right = helper(A1, start1+numleft+1, end1, A2, rootindex+1, end2) return subtreeroot root = helper(preorder, 0, len(preorder)-1, inorder, 0, len(inorder)-1) return root
-
Points to Note:
- Why is the assumption of ’no duplicates’ important? This is because with duplicate values, there is no more unique binary tree. There could be multiple different trees with same preorder and inorder sequence. It is not possible to reconstruct the original binary tree.
So given preorder and inorder, how do we proceed?
-
First value is the root node value.
-
To know where the boundary lies between left and right, we look at where the root node value lies in inorder tree. The numbers that lie before root value in inorder array belongs to left subtree and the rest lies in right subtree.
-
The same numbers lie after root value in the preorder array. The order may not be the same.
-
The numleft (the numbers lying to left of root value in the inorder sequence is preorder left and the numbers lying on the right of root value in the inorder sequence is the preorder right
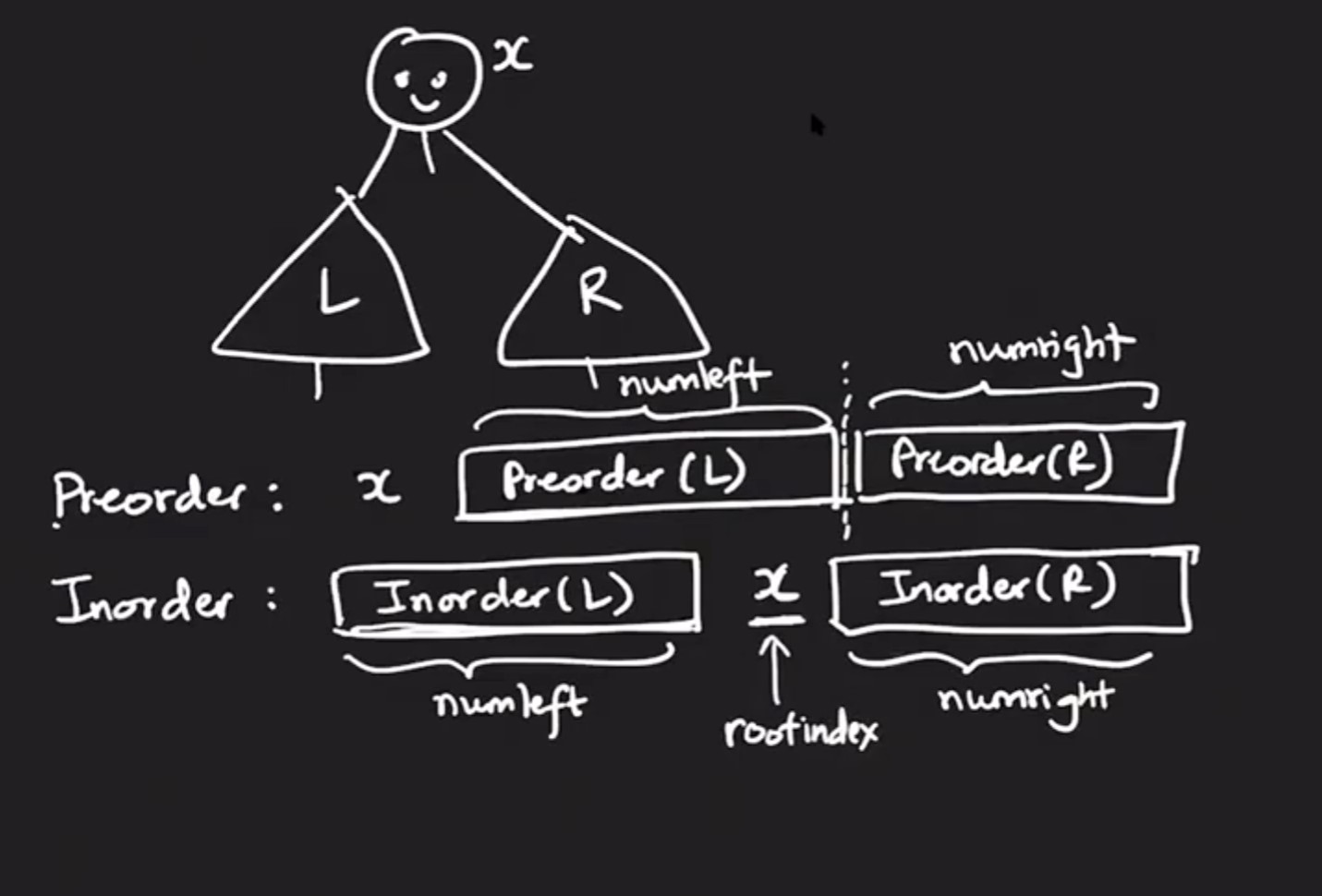
-
Complexity:
- Time complexity: Each worker creating root node, looking up hashindex and divide the subproblem. O(N) - Space Complexity: - Explicit: O(N) for hashmap and O(N) for output tree - Implicit: O(N) Since the tree may not be balanced it is not O(logN) but O(N)
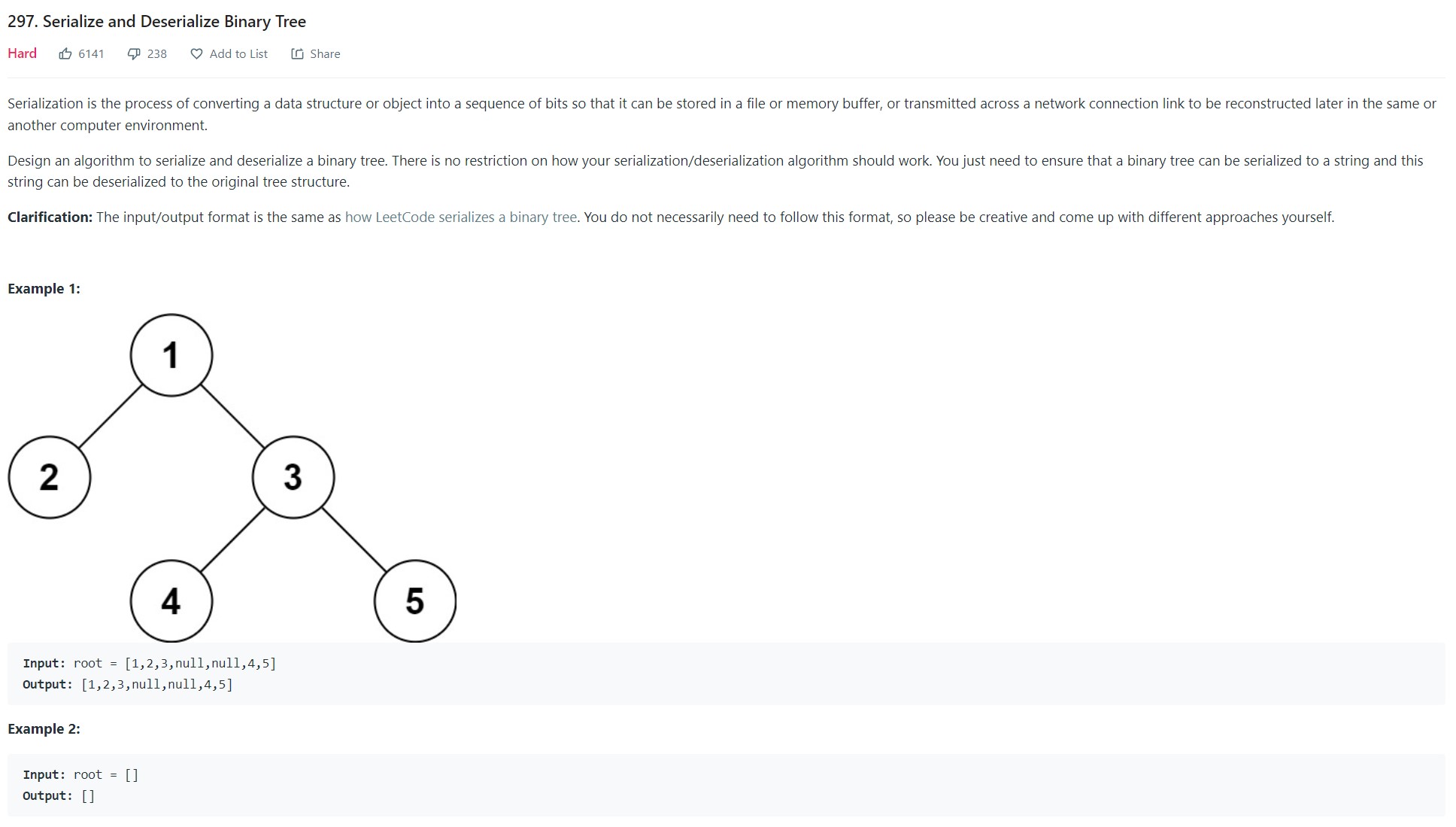
3. Serialize and Deserialize binary tree - 297 - Hard
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def isUnivalTree(self, root: Optional[TreeNode]) -> bool: if root is None: return False q = deque([root]) while len(q): node = q.popleft() if node.left is not None and node.right is not None: if node.left.val != node.right.val: return False if node.left.val != node.val: return False if node.left is not None: q.append(node.left) if node.left.val != node.val: return False if node.right is not None: q.append(node.right) if node.right.val != node.val: return False return True
- Complexity Analysis
Binary Search Tree Problems
Tree Construction
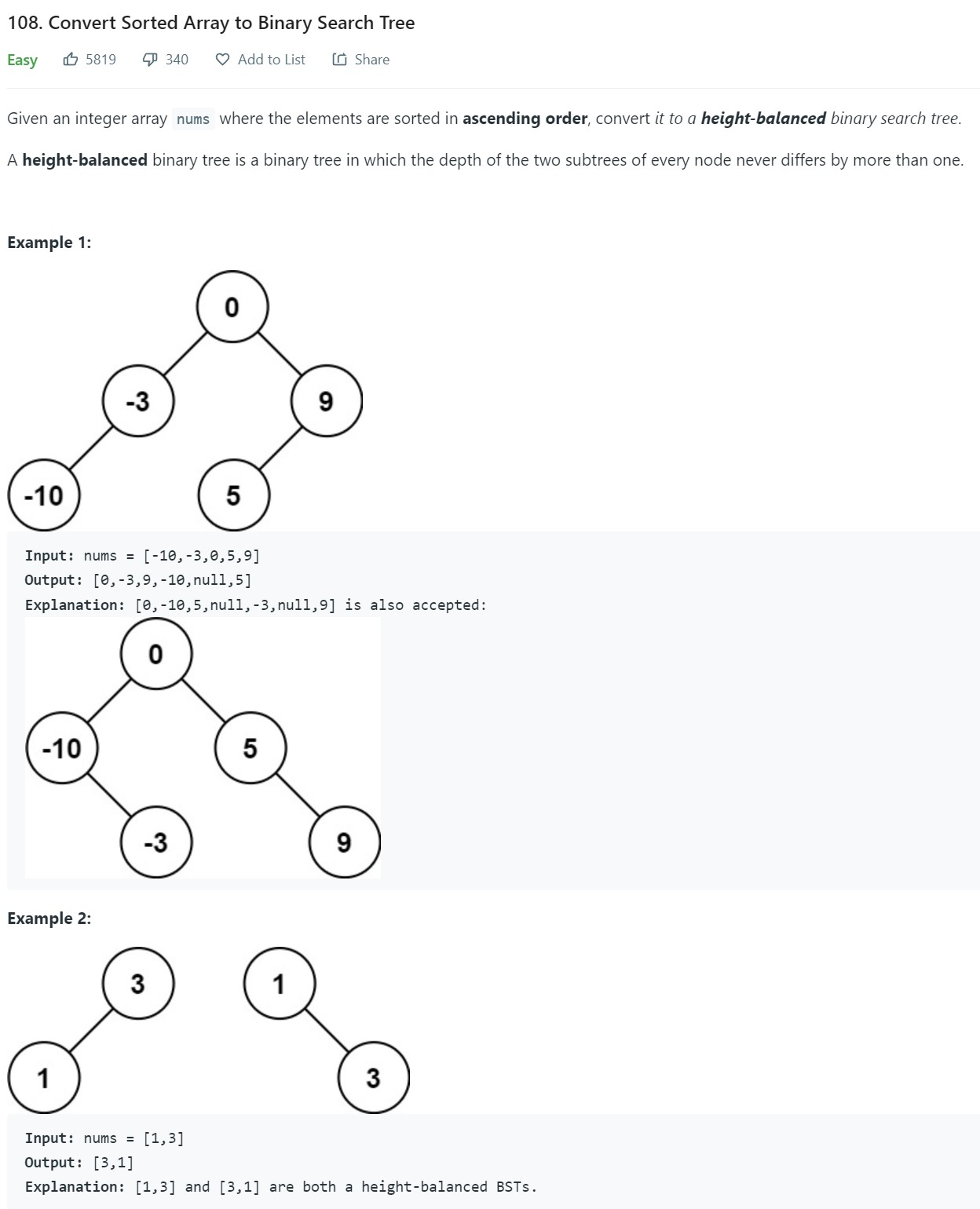
1. Convert sorted array to binary search tree - LC 108 - Easy
-
Code
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]: def dfs(A, start, end): #Base Case if start > end: return None #Recursive Case mid = start + ((end - start) // 2) root = TreeNode(val= nums[mid]) left = dfs(A, start, mid - 1) right = dfs(A, mid+1, end) root.left = left root.right = right return root root = dfs(nums, 0, len(nums) - 1) return root
- Points to Note:
-
Complexity:
-
Time complexity: O(N)
- Every worker is creating a new node and contributing to the tree. The worker takes constant time to do this. There are close to n workers resulting in \(O(n)\)
-
Space Complexity: Each worker is creating a node. Since tree is balanced, every path is bounded by O(logN) The implicit stack space is height of the tree is O(logN) The explicit space used for the output is O(N)
-
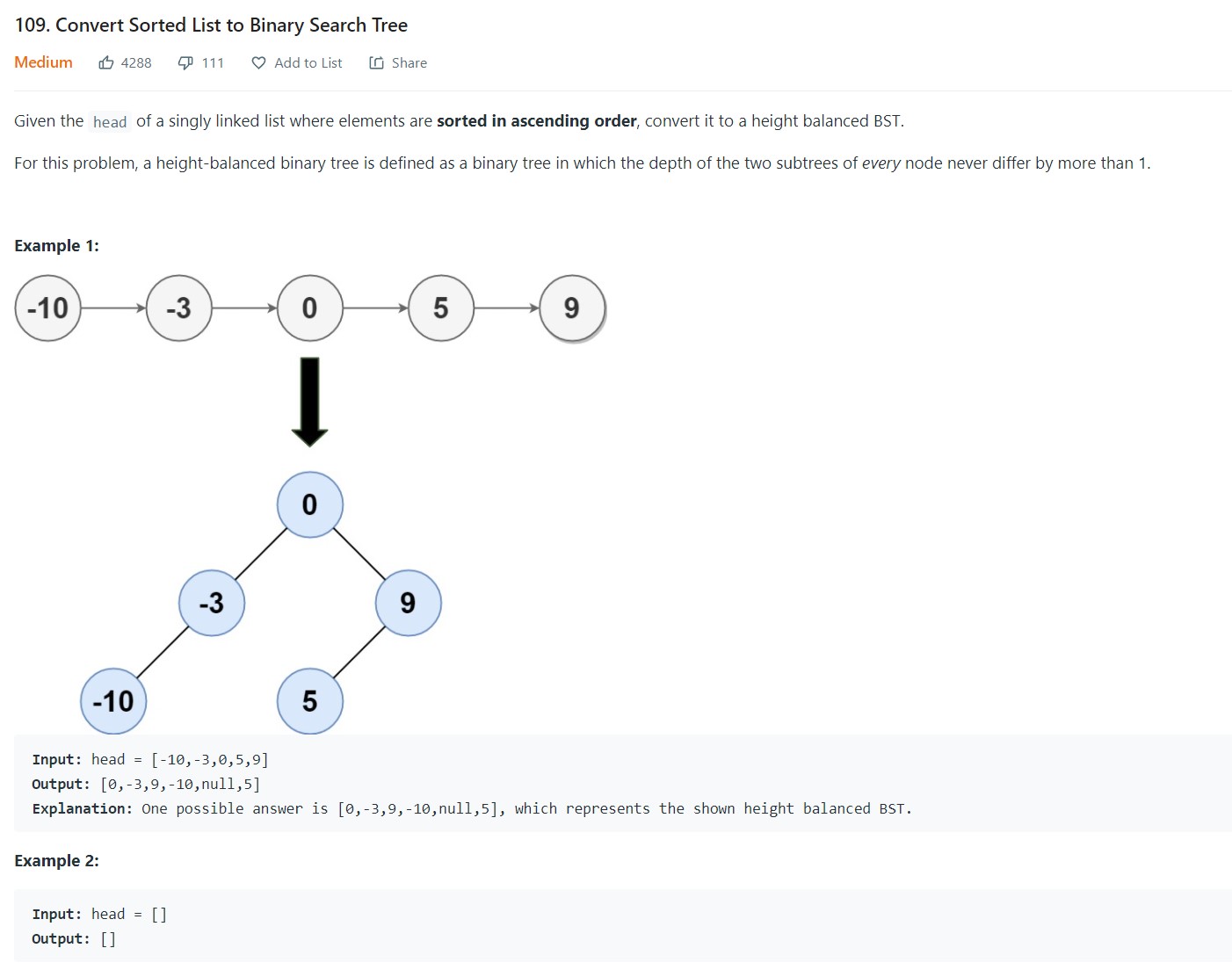
2. Convert sorted list to BST - 109 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def isUnivalTree(self, root: Optional[TreeNode]) -> bool: if root is None: return False q = deque([root]) while len(q): node = q.popleft() if node.left is not None and node.right is not None: if node.left.val != node.right.val: return False if node.left.val != node.val: return False if node.left is not None: q.append(node.left) if node.left.val != node.val: return False if node.right is not None: q.append(node.right) if node.right.val != node.val: return False return True
- Complexity Analysis
3. Convert BST To Greater Tree - 538 - Medium
4. Serialize and Deserialize BST - 449 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def isUnivalTree(self, root: Optional[TreeNode]) -> bool: if root is None: return False q = deque([root]) while len(q): node = q.popleft() if node.left is not None and node.right is not None: if node.left.val != node.right.val: return False if node.left.val != node.val: return False if node.left is not None: q.append(node.left) if node.left.val != node.val: return False if node.right is not None: q.append(node.right) if node.right.val != node.val: return False return True
- Complexity Analysis
5. Constrct BST from preorder traversal - 1008 - Medium
6. Merge Two BSTs to sorted lists [IK problem]
7. Merge two BSTs [EPI problem]
Bottom Up DFS
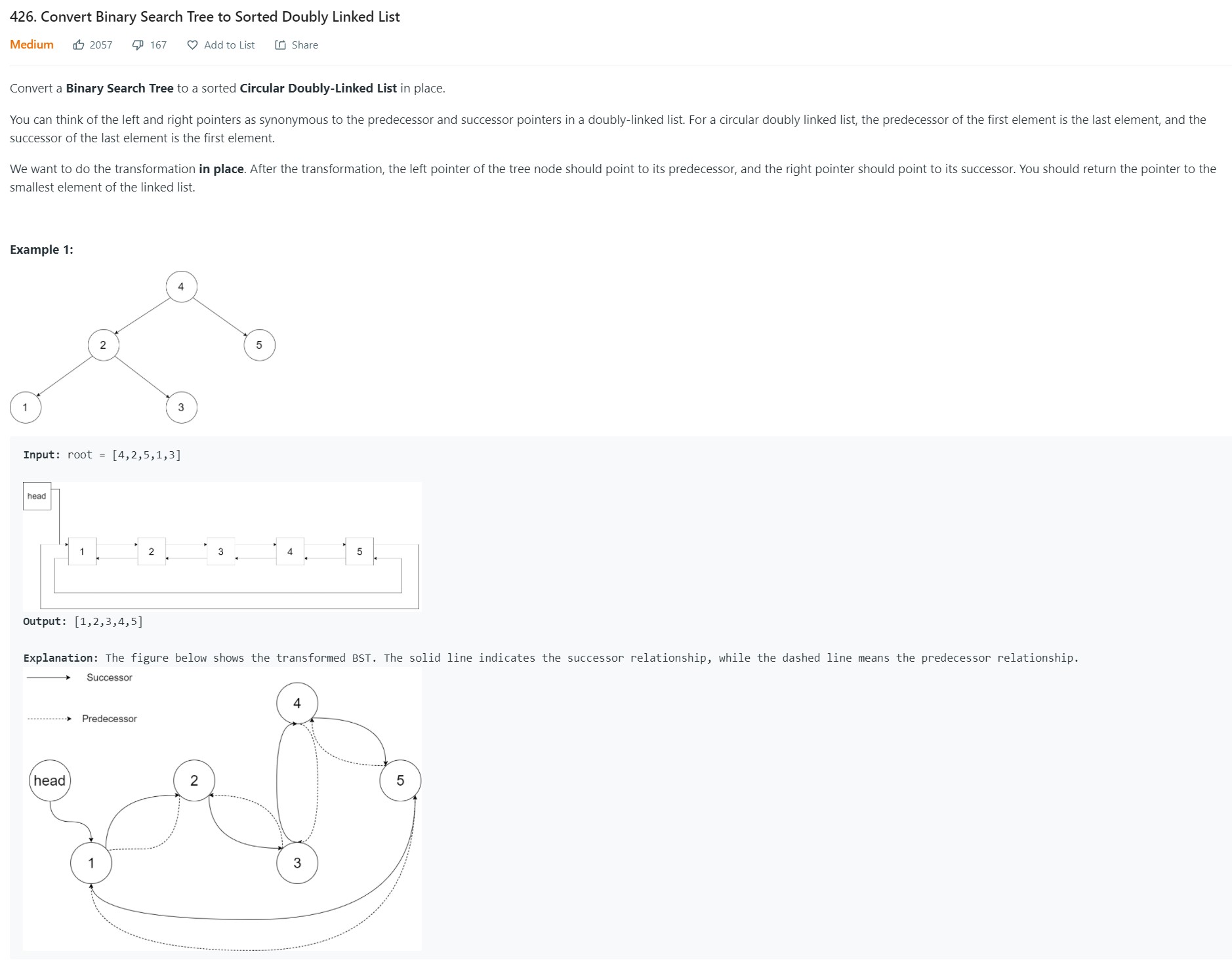
1. Convert BST to sorted doubly linked list - 426 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34""" # Definition for a Node. class Node: def __init__(self, val, left=None, right=None): self.val = val self.left = left self.right = right """ class Solution: def treeToDoublyList(self, root: 'Optional[Node]') -> 'Optional[Node]': sentinel = Node('stub') prev = [sentinel] if root is None: return None def dfs(node): if node.left is None and node.right is None: prev[0].right = node node.left = prev[0] prev[0] = node return if node.left is not None: dfs(node.left) prev[0].right = node node.left = prev[0] prev[0] = node if node.right is not None: dfs(node.right) dfs(root) head = sentinel.right head.left = prev[0] prev[0].right = head return head
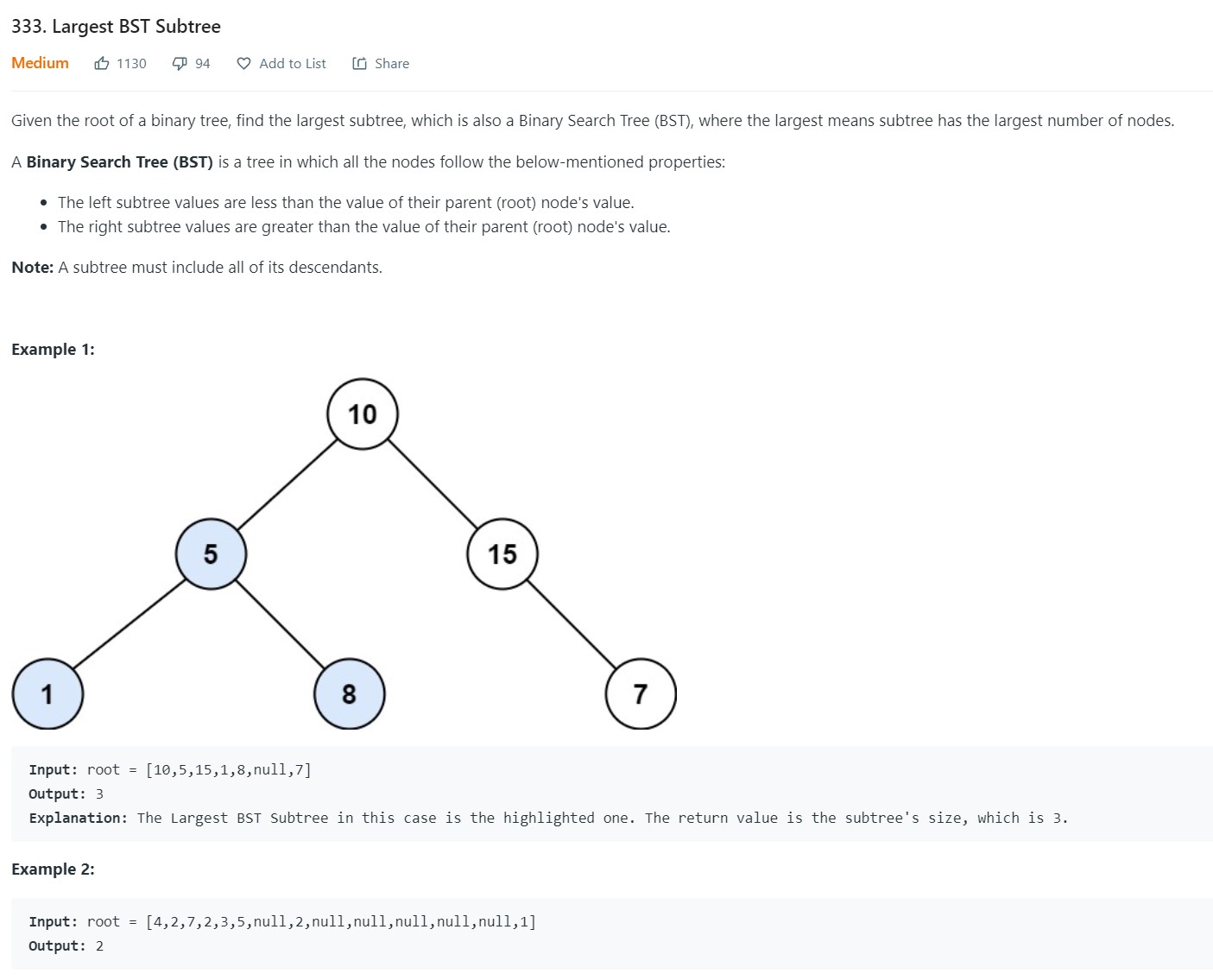
2. Largest BST Subtree - LC 333 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def largestBSTSubtree(self, root: Optional[TreeNode]) -> int: if root is None: return 0 ''' Global Problem: Find the largest BST Subtree #Local (Per-node) Problem: Am I a BST? If so, then how many nodes do I have? #Local to Global: Global solution is the max of all the local solutions which are the BSTs # To calculate local solution: - Each node has to figure out if it is a BST and # of nodes in its subtree - For this, it needs to know if its left and right subtrees are BSTs. - and the largest element in the left subtree and smallest element in its right subtree # This means, each node has to return: 1. AM I BST True or False 2. largest element in its left subtree 3. smallest element in its right subtree 4. Its total size ''' globalsize = [0] def dfs(node): mysize = 1 mysmallest = mylargest = node.val iambst = True #Base Case: Leaf node if node.left is None and node.right is None: pass #Recursive Case: if node.left is not None: (size, smallest, largest, isbst) = dfs(node.left) mysize += size mysmallest = min(mysmallest, smallest) mylargest = max(mylargest, largest) if not isbst or largest >= node.val: iambst = False if node.right is not None: (size, smallest, largest, isbst) = dfs(node.right) mysize += size mysmallest = min(mysmallest, smallest) mylargest = max(mylargest, largest) if not isbst or node.val >= smallest: iambst = False if iambst and mysize > globalsize[0]: globalsize[0] = mysize return(mysize, mysmallest, mylargest, iambst) dfs(root) return globalsize[0]
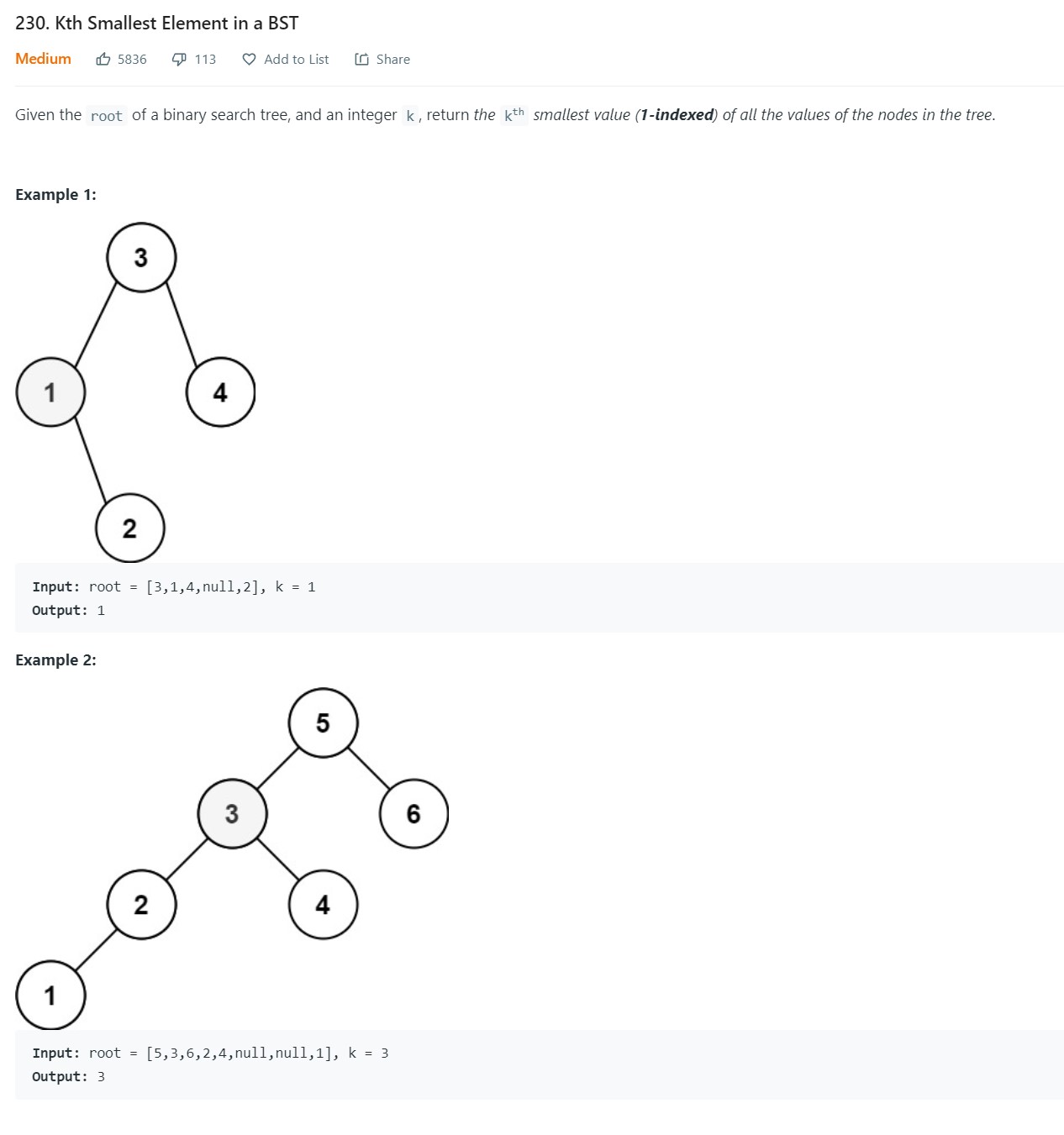
3. Kth smallest element in a BST - 230 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18class Solution: def kthSmallest(self, root: Optional[TreeNode], k: int) -> int: """ :type root: TreeNode :type k: int :rtype: int """ stack = [] while True: while root: stack.append(root) root = root.left root = stack.pop() k -= 1 if not k: return root.val root = root.right
-
Points to Note:
- To solve the problem, one could use the property of BST :
inorder traversal of BST is an array sorted in the ascending order.
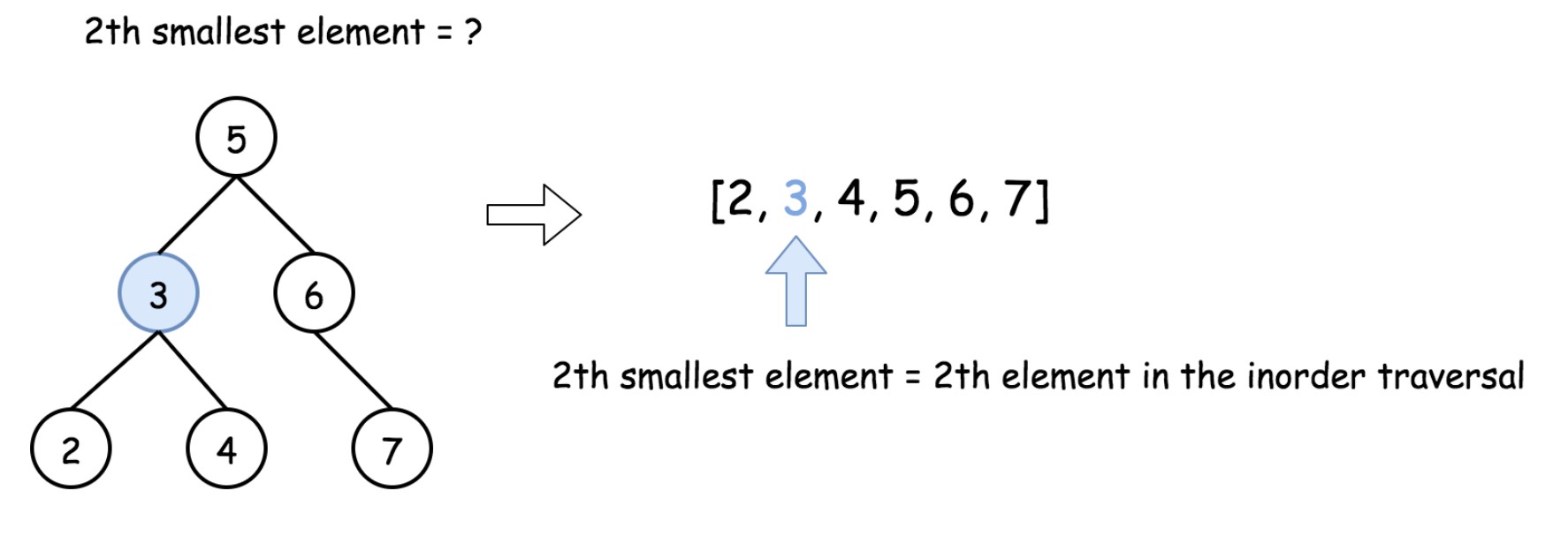
- To solve the problem, one could use the property of BST :
-
Complexity:
- Time Complexity: \(O(N)\)
- Space Complexity: \(O(N)\) The height of the tree H which in the worst case is \(O(N)\)
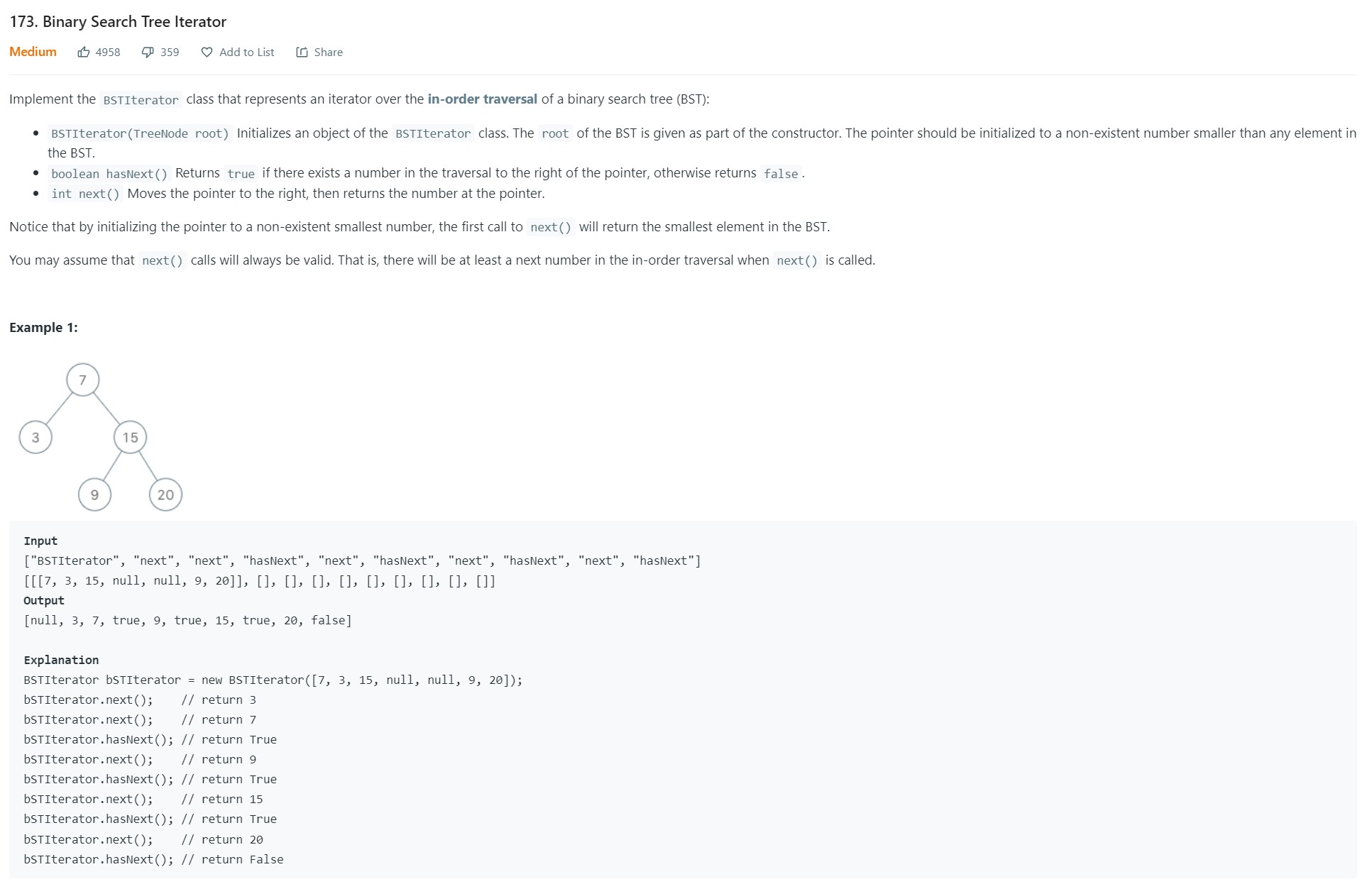
4. Binary Search Tree Iterator - 173 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def isUnivalTree(self, root: Optional[TreeNode]) -> bool: if root is None: return False q = deque([root]) while len(q): node = q.popleft() if node.left is not None and node.right is not None: if node.left.val != node.right.val: return False if node.left.val != node.val: return False if node.left is not None: q.append(node.left) if node.left.val != node.val: return False if node.right is not None: q.append(node.right) if node.right.val != node.val: return False return True
- Complexity Analysis
5. Increasing Order Search Tree - 897 - Easy
6. Recover Binary Search Tree - 99 - Medium
7. Validate Binary Search Tree - LC 98 - Medium
-
Code
def isValidBST(self, root): #Global Problem: Determine if the entire tree is BST #Local (Per node Problem): Determine if the subtree rooted at each node is BST #Local -> Global: All local problems must return True for global solution to be true #So if any local solution is false, global will become False isbst = [True] def dfs(node): ''' - A node will determine if it is BST by looking at its left and right subtrees. - The largest value in the left subtree should be smaller than the root value. - The smallest value in the right subtree should be larger than the root value. - Both subtrees should be BST - This means each node should return (smallest, largest and whether am_i_bst) values in its subtree to its parent. - The reason all three values are returned even though we do not require all of them from each side of the subtree is because we write generalized recursive function and not easy to differentiate if the node belongs to left or right subtree. ''' iambst = True smallest, largest = node.val, node.val #Base Case: Leaf NOde if node.left is None and node.right is None: pass #Recursive Case: Internal Node if node.left is not None: (s, l, b) = dfs(node.left) smallest = min(smallest, s) largest = max(largest, l) if not b or l >= node.val: iambst = False if node.right is not None: (s, l, b) = dfs(node.right) smallest = min(smallest, s) largest = max(largest, l) if not b or node.val >= s: iambst = False if iambst == False: isbst[0] = False return(smallest, largest, iambst) dfs(root) return isbst[0] # or (S, L, B) = dfs(root); return B
-
Points to Note:
-
This is a decision problem.
-
Global problem: Determine whether overall tree is BST
-
Local problem: Check whether the sub tree rooted at its node is BST or not.
-
How does the local answer affect the global answer? If the local answer is no, we can right away return False for the global problem.
-
How do we determine the sub tree rooted at a node is BST or not? Info I need:
- My left sub tree should tell me the largest value from left sub tree. This will be my predecessor.
- From right sub tree, I need the smallest value. This will be my successor
- Whether each side of the subtree is bst by itself or not.
- The general strategy every node should pass is both the smallest and the largest value. Otherwise some node is not going to get one or the other value.
- The second part is to solve the local problem. The current node’s value should have strict less than relationship with right subtree and strict greater than relationship with left subtree.
- Each node is going to return largest and smallest value though we need only one of them from each side. Omkar says Leetcode defines the local problem this way.
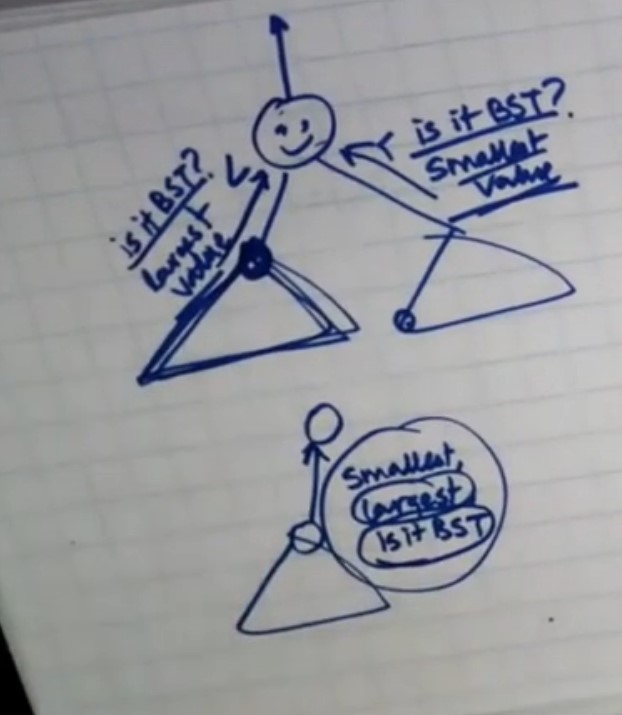
-
- Complexity:
N-Aray Tree Problems
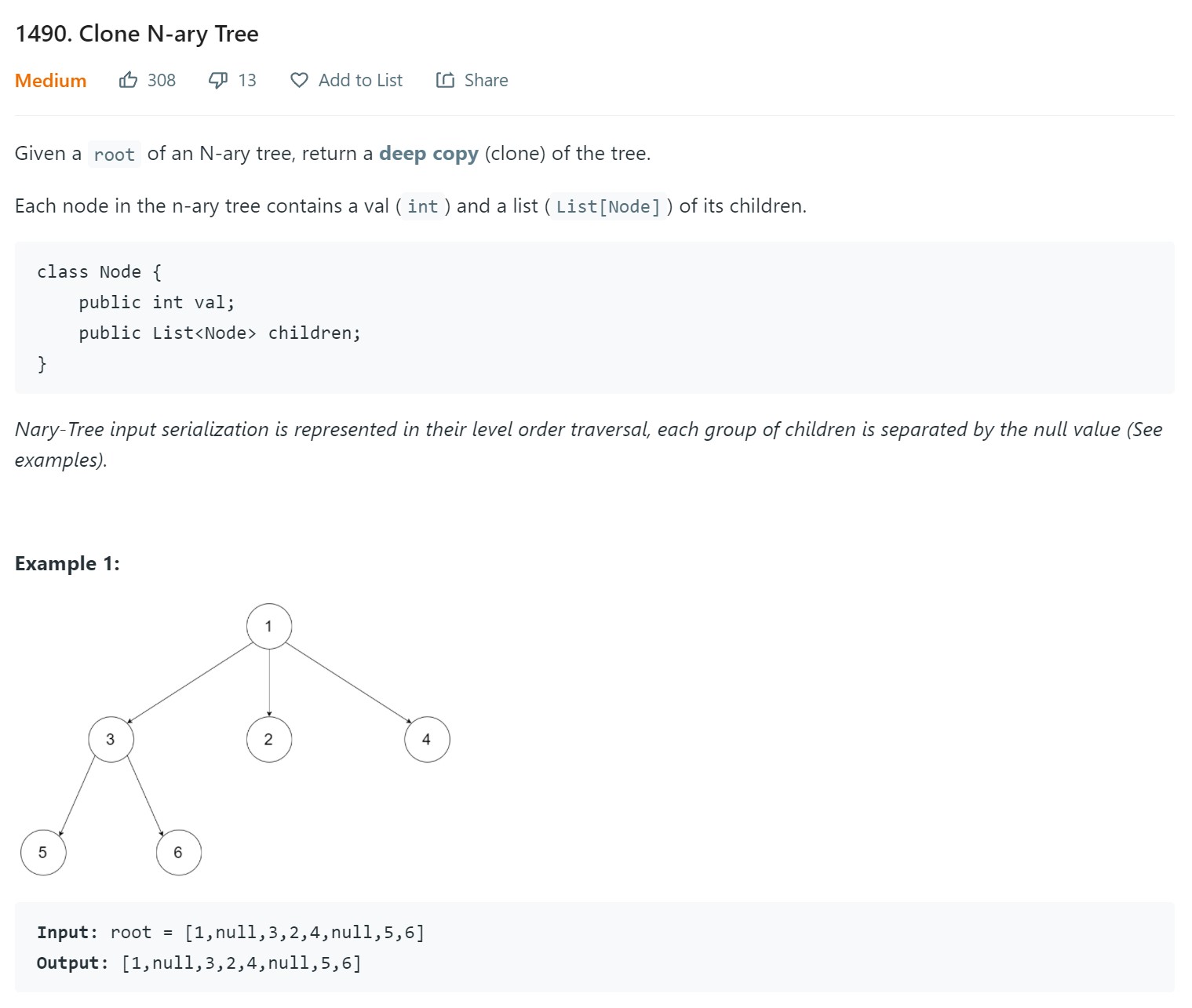
1. Clone N Aray tree - 1490 - Medium
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18class Solution: def cloneTree(self, root: 'Node') -> 'Node': if root is None: return None root_clone = Node(val=root.val) q = deque([(root, root_clone)]) while len(q): numnodes = len(q) for _ in range(numnodes): (node, node_clone) = q.popleft() for child in node.children: if child is not None: node = Node(val=child.val) node_clone.children.append(node) q.append((child, node)) return root_clone
-
Points to Note:
- Keep the root of both the trees in the queue
- Pop them together then only we will see the tree has children. Once you see a node has children, create newly created nodes as children for the new tree. Add them together to the queue.
- Insert these as tuple to the queue.
-
Complexity:
- Time Complexity: \(O(N)\)
- Space Complexity: \(O(N)\)
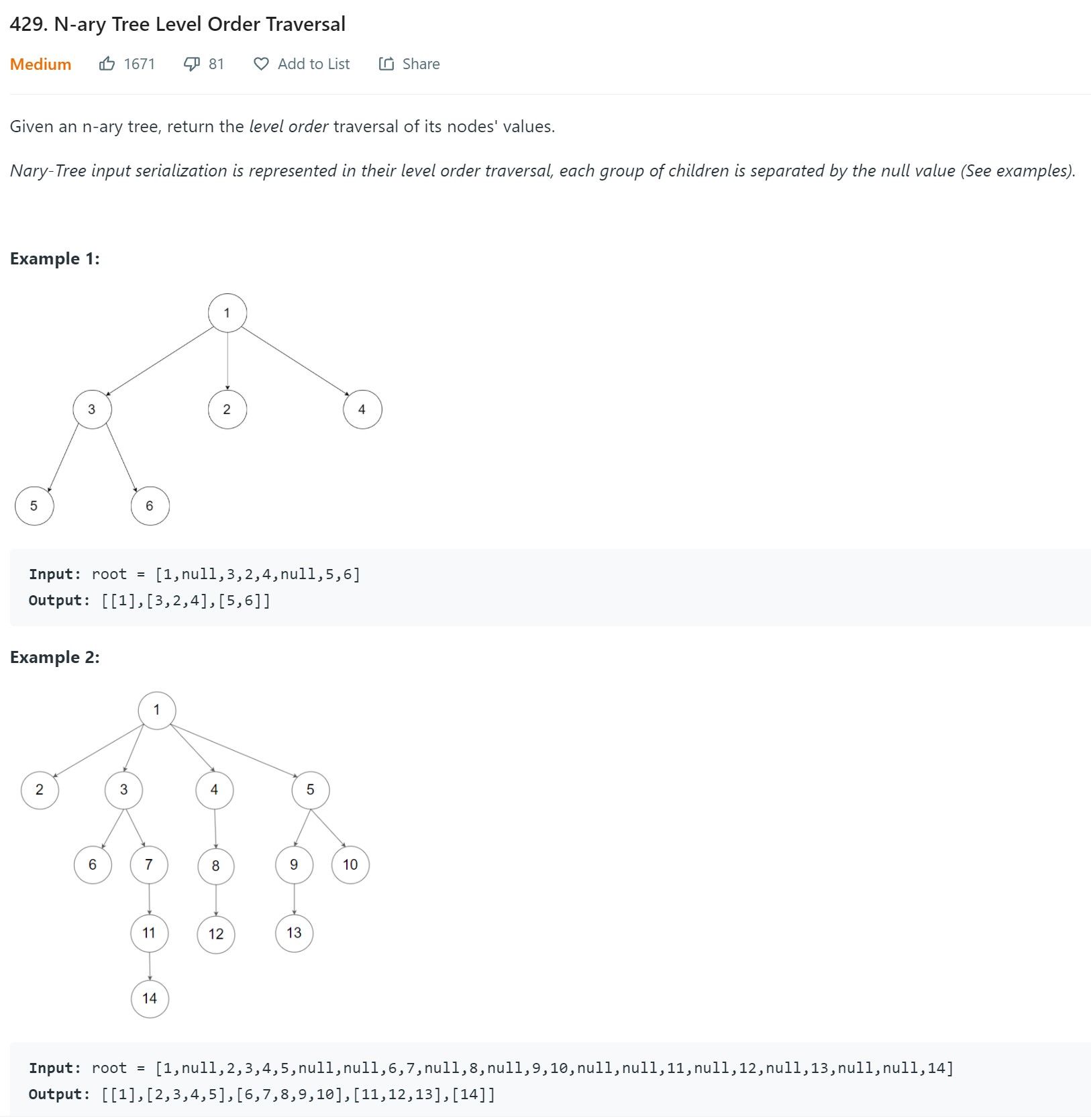
2. N-ary Tree Level Order Traversal - LC 429 - Medium
-
Code
class Solution: def levelOrder(self, root: 'Node') -> List[List[int]]: result = [] if root is None: return [] q = collections.deque([root]) while len(q): temp = [] numnodes = len(q) for _ in range(numnodes): node = q.popleft() temp.append(node.val) for i in node.children: if i is not None: q.append(i) result.append(temp) return result
-
Points to Note
- It may look like we have three inner loops but still time complexity is O(N)
- For level order traversal, if we need to get a list of children at each level, we need a loop for every level and another loop to add children of each level.
- The number of nodes related to edges is edges -1 (because root has no unpaired node and every other edge is paired) applies for binary and n-aray trees
- Complexity Analysis
3. Maximum Depth of N-ary Tree - LC 559 - Easy
-
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24""" # Definition for a Node. class Node: def __init__(self, val=None, children=None): self.val = val self.children = children """ class Solution: def maxDepth(self, root: 'Node') -> int: if root is None: return 0 q = deque([root]) max_depth = 0 while len(q): numnodes = len(q) max_depth += 1 for _ in range(numnodes): node = q.popleft() for child in node.children: q.append(child) return max_depth
References:
Omkar Slides: